二叉树的左旋与右旋

对于在一颗结点和层数比较多的二叉树上查找一个元素时，二叉排序树的查找效率远远高于一颗普通的树。
如下为普通二叉树和二叉排序树：

假设查找结点20

/*** 二叉树结点*/
public class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}public TreeNode(int val) {this.val = val;}

在普通二叉树上查找：

 //查找结点static int ct = 0;//记录比较次数public static boolean isExistTreeNode(TreeNode root, TreeNode target){if(root == null) return false;if(root.val == target.val) return true;ct ++;return isExistTreeNode(root.left,target) || isExistTreeNode(root.right, target);//普通查找}

在平衡二叉树上查找：

    //查找结点static int ct = 0;public static boolean isExistTreeNode(TreeNode root, TreeNode target){if(root == null) return false;if(root.val == target.val) return true;ct ++;return target.val>root.val?isExistTreeNode(root.right,target):isExistTreeNode(root.left,target);//利用二叉排序树特点进行查找}

 public class Main {public static void main(String[] args) {TreeNode node1 = new TreeNode(8);TreeNode node2 = new TreeNode(10);TreeNode node4 = new TreeNode(15);TreeNode node5 = new TreeNode(20);TreeNode node6 = new TreeNode(25);TreeNode node7 = new TreeNode(30);//        node4.left = node2;//        node2.left = node1;//        node2.right = node5;//        node4.right = node7;//        node7.right = node6;////        isExistTreeNode(node4,new TreeNode(20));//        System.out.println(ct); //比较次数为2node2.left = node1;node2.right = node5;node5.left = node4;node5.right = node7;node7.left = node6;isExistTreeNode(node4,new TreeNode(20));System.out.println(ct);//比较次数为1}
}

可以发现在普通二叉树上查找需要比较两次，二而二叉排序树上则只要一次。
(上面两颗树的结点和层数比较少，效果无法太明显体现出来，感兴趣的话可以尝试一下随机构建一颗层数和结点多普通二叉树，和二叉排序树来测试)

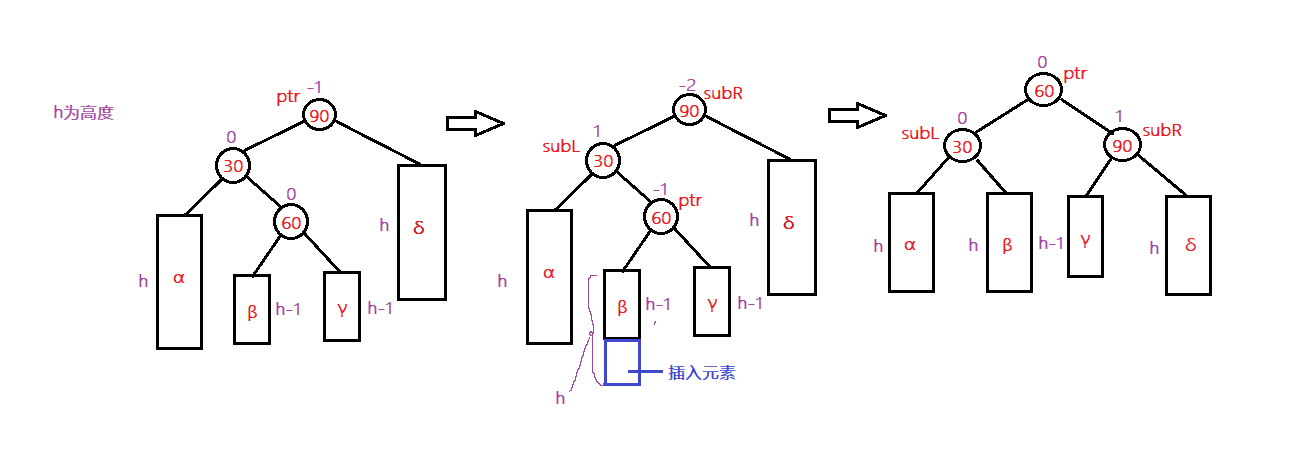
但是构建一颗的二叉排序树时，有时候某个结点的左子树远远深于右子树或者相反，此时我们会发现假设要查找的节点在比较深的子树时，比较次数还是会比较多，如何充分发挥二叉排序树的作用呢，二叉平衡排序树就出来了。

二叉平衡排序树

定义：一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树的树。在此基础上的平衡二叉树就是二叉平衡排序树。
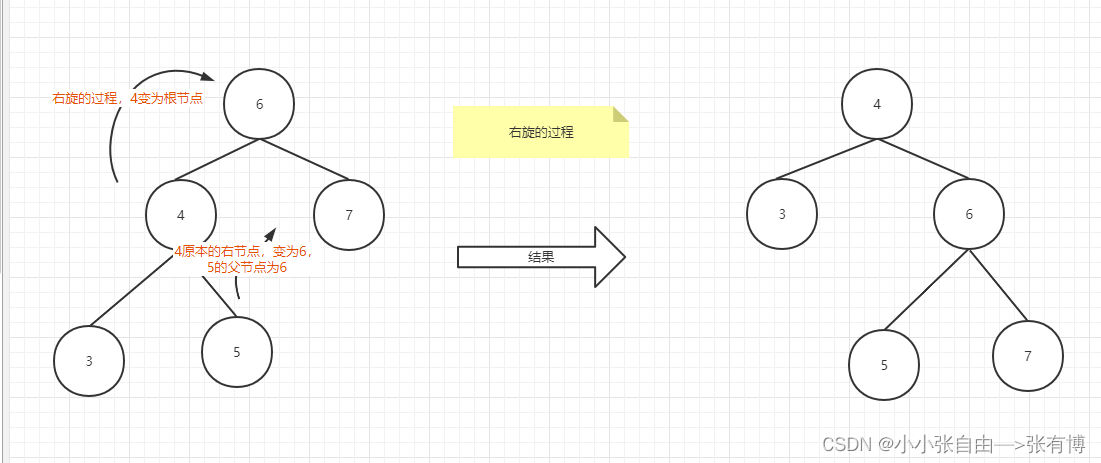
如何将一颗二叉不平衡排序树变成一颗二叉平衡排序树呢？答案就是单旋（左旋|右旋）
单旋（左旋|右旋）

下面就是一个左旋的图示：

对于该树，是一颗不平衡的书，右边深，需要左旋，将根节点右子树节点作为根节点，右子树的左子树过继给原来根节点的子节点。从而实现左旋。右旋也大同小异。
代码实现：

以上面的树为例

	//树结点public class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}public TreeNode(int val) {this.val = val;}}

    //判断二叉树是否平衡的public static boolean isBalance(TreeNode root){if(root == null) return true;int leftDeep = getDeep(root.left);int rightDeep = getDeep(root.right);if(Math.abs(leftDeep - rightDeep) > 1) return false;return isBalance(root.left) && isBalance(root.right);}//构建平衡二叉树public static TreeNode toBalanceTree(TreeNode root){if(root == null) return null;root.left = toBalanceTree(root.left);root.right = toBalanceTree(root.right);int leftDeep = getDeep(root.left);int rightDeep = getDeep(root.right);if(leftDeep - rightDeep > 1){//不平衡 左边深，需要右旋return rightRotate(root);}else if(rightDeep - leftDeep > 1){//不平衡 右边深， 需要左旋return leftRotate(root);}return root;}//左旋public static TreeNode leftRotate(TreeNode root){TreeNode originRoot = root;TreeNode newRoot = root.right;TreeNode tempBranch = newRoot.left;newRoot.left = originRoot;originRoot.right = tempBranch;return newRoot;}//右旋public static TreeNode rightRotate(TreeNode root){TreeNode originRoot = root;TreeNode newRoot = root.left;TreeNode tempBranch = newRoot.right;newRoot.right = originRoot;originRoot.left = tempBranch;return newRoot;}//求二叉树的深度public static int getDeep(TreeNode root){if(root == null) return 0;int leftDeep = getDeep(root.left);int rightDeep = getDeep(root.right);return leftDeep>rightDeep?leftDeep+1:rightDeep+1;}

public class Main2 {public static void main(String[] args) {/*** 单旋测试*///构建二叉树TreeNode node1 = new TreeNode(10);TreeNode node2 = new TreeNode(15);TreeNode node3 = new TreeNode(20);TreeNode node4 = new TreeNode(30);TreeNode node5 = new TreeNode(25);TreeNode node6 = new TreeNode(8);node1.right = node3;node1.left = node6;node3.left = node2;node3.right = node4;node4.left = node5;System.out.println(isBalance(node1));//falseTreeNode newRoot = toBalanceTree(node1);System.out.println(isBalance(newRoot));//trueSystem.out.println("构建完成");//debug一下}