红黑树简介及左旋、右旋、变色

红黑树(Red Black Tree)是一种自平衡二叉搜索树(二叉查找树)，是一种特殊的二叉搜索树，在进行插入和删除时通过特定操作保持二叉树自身的平衡，从而获得较高的查找性能。

红黑树的平衡操作通过左旋、右旋和变色来实现，平衡的过程是比较复杂的，但通过平衡操作，可以获得更高效的性能。对二叉搜索树进行平衡后，最坏情况的运行时间得到优化，可以在O(logN)的时间复杂度内完成查找、插入和删除，N是二叉搜索树中的节点数。

一、二叉搜索树的性能分析

红黑树是一种特殊的二叉搜索树，所以本文先从二叉搜索树说起。

二叉搜索树是一种特殊的二叉树，具有如下特性：

1. 如果二叉树的左子树不为空，则左子树上所有节点的值均小于它的根节点的值。

2. 如果二叉树的右子树不为空，则右子树上所有节点的值均大于它的根节点的值。

3. 如果独立地看，左子树、右子树也分别为二叉搜索树。

二叉搜索树的实现，可以参考：Python实现二叉搜索树_小斌哥ge的博客-CSDN博客

向二叉搜索树中插入数据时，为了满足二叉搜索树的特性，会递归地比较插入节点的值与根节点的值，将数据插入正确的位置。

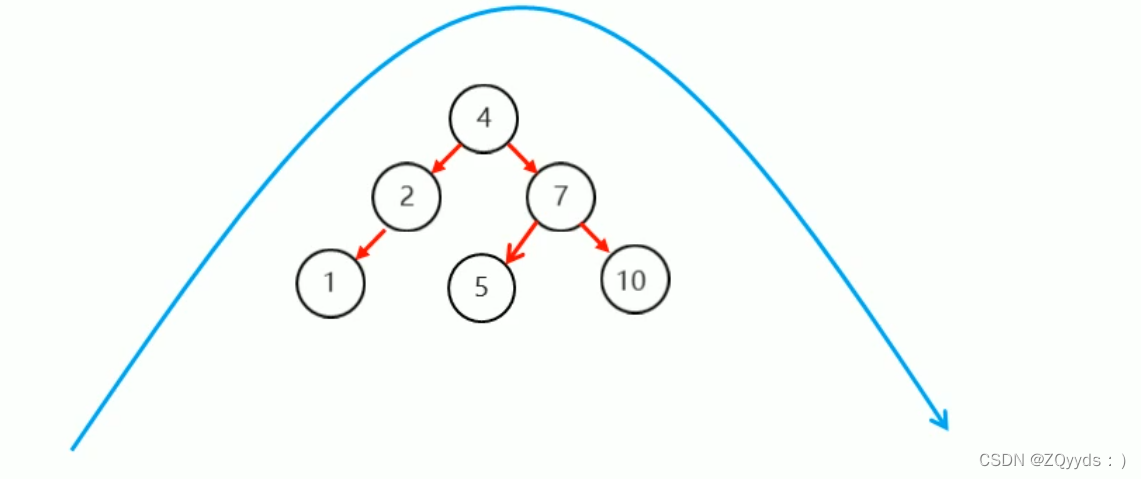
如在一棵空二叉搜索树中插入 [50, 77, 55, 29, 10, 30, 66, 80, 51, 18, 90] ，得到的二叉搜索树结构如下图：

从结构图可以看出，这棵二叉搜索树是平衡的，当在二叉搜索树中查找数据时，按照二分法查找的思想，从根节点开始，然后到子树中进行查找，如果没有查找到目标数据，每次都会往树的下一层进行查找，需要的最大查找次数等于树的深度。最坏的情况就是找到树的最深一层，所以在这棵树中查找的最坏情况是查找4次。

还是上面例子中的数据，假设比根节点50大的数据是升序排列的，如 [50, 51, 55, 66, 77, 80, 90, 29, 10, 30, 18] ，比根节点50小的数据顺序不变，将这些数据插入到二叉搜索树中，得到的二叉搜索树结构如下图：

很明显，这棵二叉搜索树是不平衡的。在这棵树中查找数据的最坏情况需要查找7次，查找次数多的原因就是树的不平衡，右子树一直在往深度上延伸。如果把根节点和右子树拿出来，结构如下图：

根据结构图，这是一棵右斜树。它虽然是一棵二叉树，但它更像是一个链表，正在向链表“退化”。链表的时间复杂度是O(N)，平衡二叉树的时间复杂度是O(logN)，当N很大的时候，O(N)与O(logN)的性能差距是很大的。

可见，二叉搜索树的插入顺序会影响到树的结构，从而影响性能。对于上面的例子，总共只有11个节点，出现7个数据顺序排列的可能性不大，但在实际的应用场景中，节点可能是110个，11000个，11000000个，甚至更多。在数据量增大的时候，这些数据中出现一段或多段数据顺序排列的可能性是很大的，这就会造成二叉搜索树极度不平衡，向链表退化，性能大大降低。

所以，保持二叉搜索树的平衡，对性能的保证有至关重要的作用。由于数据是动态变化的，会动态地增加或减少，不可能在构造二叉搜索树前控制数据的排列顺序。要保持二叉搜索树的平衡，就要在每增加一个节点或每减少一个节点时都保持平衡，即让二叉搜索树一直保持平衡，这样二叉搜索树的性能就不可能向链表退化。

当二叉搜索树中的节点数量发生改变时，使用一些策略来保持平衡，红黑树就是这样一种二叉树。

二、红黑树简介

红黑树是一种自平衡二叉搜索树，每个节点都有颜色，颜色为红色或黑色，红黑树由此得名。除了满足二叉搜索树的特性以外，红黑树还具有如下特性：

1. 节点是红色或黑色。

2. 根节点是黑色。

3. 所有叶子节点都是黑色的空节点。(叶子节点是NIL节点或NULL节点)

4. 每个红色节点的两个子节点都是黑色节点。(从每个叶子节点到根的所有路径上不能有两个连续的红色节点)

5. 从任一节点到其每个叶子节点的所有路径都包含相同数目的黑色节点。

要知道什么是红黑树，必须记住这5条特性。这5条特性其实是5条规定，只有满足这5条规定才属于红黑树。对于二叉搜索树的特性，只要理解了，很容易记住，但对于红黑树的5条特性，需要“死记硬背”。

如上面例子中的二叉搜索树，可以加上颜色变成一颗红黑树。(实际的红黑树是一个节点一个节点插入的，如下的构造过程只是为了先理解红黑树的5条特性)

1. 先加上叶子节点，并把所有节点都标记为黑色。

2. 这棵二叉树显然不满足红黑树的特性5，如节点10到左子树的叶子节点的路径上有一个黑节点，到右子树的叶子节点的路径上有两个黑节点，所以要将一些黑节点变成红节点。

从根节点50开始，使根节点到每个叶子节点的路径上都有4个黑节点，得到的红黑树如下。

当然，也可以使根节点到每个叶子节点的路径上都有3个黑节点，得到的红黑树如下。

现在看一下这两棵树是否满足红黑树的5条特性，可以一条一条的对比，至于构造的过程先不管(这其实是硬拼出来的)，后面再讲怎么构造。

根据红黑树的特性5，任意节点到其所有叶节点的路径上的黑节点数都相同，从而保持红黑树的平衡。如果只看黑节点，这种平衡是完美的平衡，所以红黑树的平衡也称为黑色完美平衡。当然，因为红节点的存在，红黑树并不是完美平衡的，甚至有可能不满足平衡二叉树的特性。

当在红黑树中插入节点或删除节点时，红黑树的平衡很可能会被破坏(不满足其中一条或多条特性)，要立即对红黑树进行调整，使红黑树重新满足5条特性。

调整平衡的操作包含左旋、右旋和变色，下面依次对这些操作进行介绍。

三、红黑树的左旋和右旋操作

对于一棵红黑树，它满足红黑树的5条特性。插入或删除节点之后，红黑树就发生了变化，很可能不再完全满足红黑树的5条特性了，也就是不再是一棵红黑树了，而是一棵普通的二叉搜索树。这时候，为了使二叉搜索树重新变成红黑树，就需要对二叉搜索树进行操作，使它满足红黑树的5条特性。

通过旋转，可以使二叉搜索树重新满足红黑树的5条特性。旋转分为左旋和右旋。

1. 红黑树的左旋

左旋：以某个节点作为支点(旋转节点)，其右子节点变为旋转节点的父节点，右子节点的左子节点变为旋转节点的右子节点，旋转节点的左子节点保持不变。右子节点的左子节点相当于从右子节点上“断开”，重新连接到旋转节点上。

为了不失一般性，可以看下图中的例子。左边是左旋前的红黑树局部结构，先不考虑整体，只看局部，左旋前不满足红黑树的特性5。

左旋时，旋转节点为节点50，左旋后，旋转节点的右子节点70变为旋转节点50的父节点，右子节点的左子节点60从右子节点70上“断开”，成为旋转节点50的右子节点。

左旋后，结构如右图，这个局部重新满足了红黑树的特性5，达到目的。

再看另一个左旋的例子，左边是左旋前的局部结构，以节点10作为旋转节点，左旋后，旋转节点的右子节点20成为旋转节点10的父节点，右子节点的左子节点(这里是一个叶子节点NIL)从右子节点上“断开”，成为旋转节点10的右子节点。

2. 红黑树的右旋

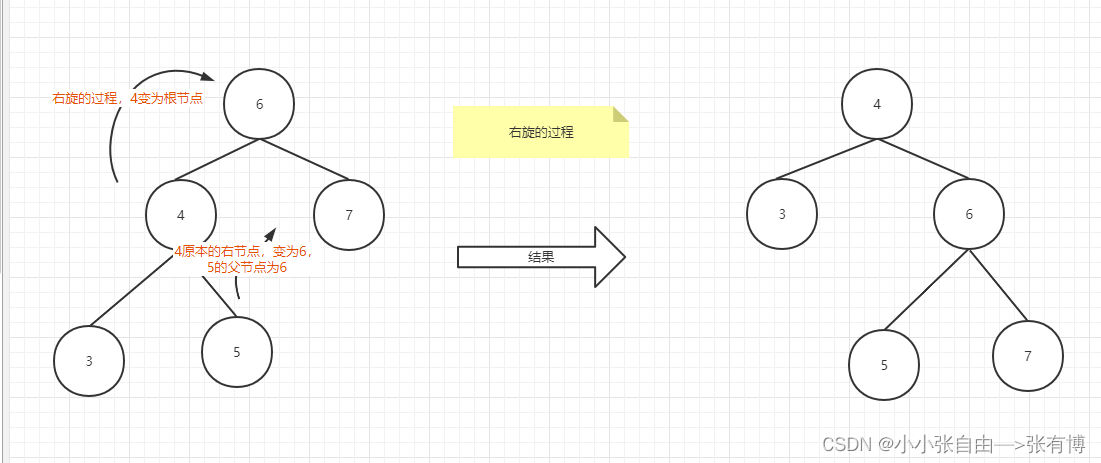
右旋：以某个节点作为支点(旋转节点)，其左子节点变为旋转节点的父节点，左子节点的右子节点变为旋转节点的左子节点，旋转节点的右子节点保持不变。左子节点的右子节点相当于从左子节点上“断开”，重新连接到旋转节点上。

不难看出，左旋和右旋是相反的，可逆的。

下图中的例子仍然是红黑树的局部，左边的结构不满足红黑树的特性5。

右旋时，旋转节点为节点70，右旋后，旋转节点的左子节点50变为旋转节点70的父节点，左子节点的右子节点60从左子节点50上“断开”，成为旋转节点70的左子节点。右旋后(右图)，重新满足了红黑树的特性5。

同样再看一个右旋的例子，左边是右旋前的局部结构，以节点30作为旋转节点，右旋后，旋转节点的左子节点20成为旋转节点30的父节点，左子节点的右子节点(这里是一个叶子节点NIL)从左子节点上“断开”，成为旋转节点30的左子节点。

通过对左旋和右旋的介绍和举例，左旋和右旋的目的都是通过旋转节点的方式使二叉搜索树重新满足红黑树的特性，左旋和右旋是互逆的，根据不同的情况使用不同的旋转方式。

四、红黑树的变色操作

当对红黑树进行插入或删除节点之后，如果不再完全满足红黑树的5条特性，除了旋转，变色也可以使二叉搜索树重新满足红黑树的5条特性。

变色：将节点的颜色由红变黑或由黑变红。

向红黑树中插入节点时，新节点的颜色都设置为红色。不管新节点是什么颜色，特性3都不可能被破坏，特性1、2、4都有可能被破坏。如果插入的节点是黑色，则一定会破坏特性5，需要进行调整，如果插入的节点是红色，则一定不会破坏特性5。所以将新节点设置为红色，可以降低破坏红黑树特性的可能性。

1. 添加节点

如下的左图是红黑树的一个局部，一开始是满足红黑树的特性的，在其中插入了红色节点10，两个红节点连在一起了，不再满足红黑树的特性4。

通过变色，先将节点20变成黑色，特性4满足了，但又不满足特性5，所以继续将节点30变成红色，节点40变成黑色。

经过3次变色后，从局部看，已经重新满足了红黑树的特性。但是，从整棵树来看，还不一定满足红黑树的特性，如果节点30的父节点也是红色，则还需要继续对这棵树进行调整(上面的左旋和右旋例子中也有这种情况)。

2. 删除节点

如下的左图是红黑树的一个局部，一开始是满足红黑树的特性的，将节点90删除后，不再满足红黑树的特性5。

通过变色，先将节点80变成黑色，但仍不满足特性5，继续将节点70变成红色，重新满足了红黑树的特性。

经过两次变色，重新满足了红黑树的特性，对于这个例子，只要局部满足了，整棵树一定是满足红黑树的。

五、红黑树的旋转和变色综合案例

上文中介绍旋转和变色时，是独立对它们进行分析的。这两种调整方法都可以使被破坏规则的红黑树重新满足红黑树的特性，更多的时候，需要灵活地配合使用，使调整更高效。

下面来看一个简单的例子。使用文章开头的红黑树，结构如下图。

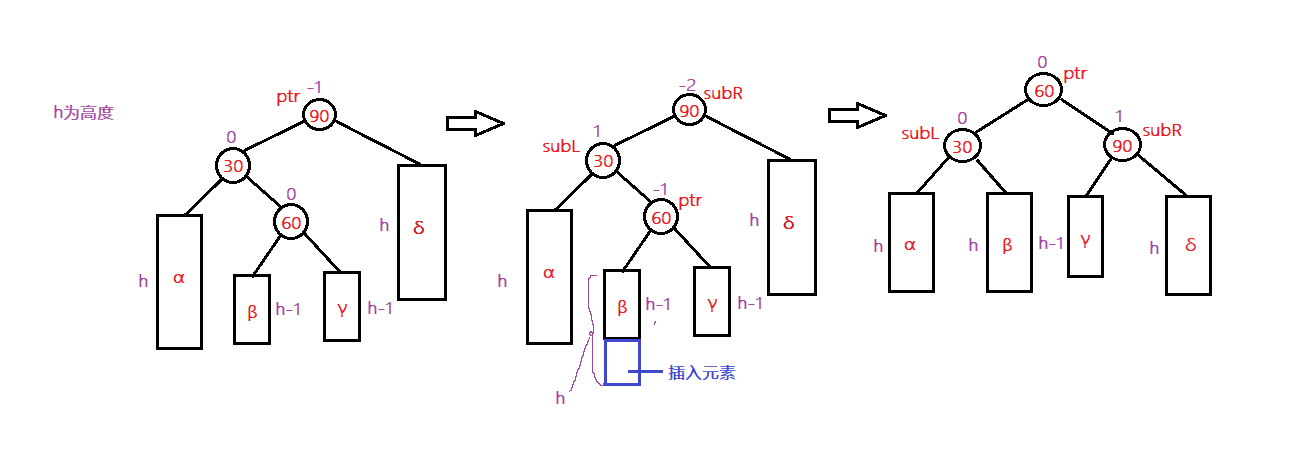
1. 在红黑树中插入节点20，插入后不满足红黑树的特性4。

2. 将节点18从红色变成黑色，变色后不满足红黑树的特性5。

3. 以节点10作为旋转节点，进行左旋，左旋后还是不满红黑树的特性5。

4. 将节点10从黑色变成红色，变色后，重新满足了红黑树的5条特性。

经过变色，左旋，变色，三个步骤之后，插入节点后的树重新成为一棵红黑树。

本文中举例的结构图是为了方便理解红黑树以及红黑树的旋转和变色，一棵真正的红黑树是一个节点一个节点地插入而得到的，并一定能得到上面图形里的这些结构。对于红黑树的插入、删除和代码实现，本专栏的其他文章会继续介绍。