本文章是我的库存文章，本来不发的，但还是发吧，请跳到第7节，那才是讲左旋和右旋的。至于前面的复习树要看也可以，只是一堆概念，并不复杂。

复习树

1. 树的概念

  生活中的树跟程序中的树其实大同小异，比如生活中的树是不是有树根，在树根的基础上是不是会有分叉，而在这些分叉中是不是也可能会继续分叉，而在这些分叉上是不是也可能会生出叶子。
  对比第一段的描述，程序中的树也是如此，它也有根，也会分叉，当然也有叶子。只不过它是倒着的树，如下：

图1：

术语：

• 结点：就是图1的每一个元素。
• 前件/后件：以图1为例，元素2的前件就是元素5，后件就是元素1和元素3。
• 根结点：在树结构中，只有一个结点没有前件，该结点就为根结点。比如图1的数字5，可以把它想象成一个倒着的树，既然是倒着的，那么树根是不是就在上面。
• 父结点：在树结构中，每个结点只有一个前件，这个前件就是该结点的父结点。
• 子结点：在树结构中，每个结点可以有多个后件，这些后件就是该结点的子结点。
• 叶子结点(终端结点)：在树结构中，没有后件的结点称为叶子结点（生活中的叶子不能分叉）。
• 分支结点(非终端结点)：除了叶子结点以外的结点。
• 度：树中一个结点的子结点个数称为该结点的度，树中结点的最大度数称为树的度。
• 树的深度：在树结构中，根结点所在的层次为1，其他结点所在的层次为其父结点所在的层次加1，最大的层次称为树的深度。
• 子树：以图1为例，整个就是一颗树，那么在这颗树中又可拆分为一个子树，就好像在生活中你拔了一根树枝回家当玩具，插在泥土上，然后指着它对你的朋友说：“你看，它是一颗树”。所以，在图1中，我们能不能把它中的元素为2,1,3的结点拆分出来成为它的一颗子树？那么相应的，结点为8和7的也可以拆分出来成为一颗子树。

注意：
  一个结点也可以是一个树，也就是该树的度为0。

2. 二叉树(Binary Tree)

  二叉，二叉，顾名思义就是一个结点分了两个叉，叫二叉，但是注意，不是一定就要分两个叉，你分一个叉，甚至不分叉都可以，就是不能分两个叉以上的叉，比如三叉肯定不行，也就是说，要满足二叉树的话，你的度就只能是0，或者1，或者2。
  二叉树是在树的概念上延伸出来的，它规定了你这个结点最多只能有两个子结点，通常一个在左，一个在右，那么我们就把在左边的那个结点称为左子树，右边的那个结点就是右子树，注意，这种左右子树只存在二叉树中，比如你来个四叉树我怎么给它分左右子树。还有最后注意次序不能颠倒，也就是说它是严格分左右的，左就是左，右就是右，即使你这个结点只有一个子树，也要分左右。

存储结构：
  二叉树的存储结构分为顺序存储和链式存储：

• 顺序存储：二叉树的顺序存储就是用一组连续的存储单元存放二叉树中的结点元素，一般按照自上而下，自左向右的顺序存储。以图1为例，就是528137。但是注意，如果有空元素，要为空元素留出空间。
• 链式存储(*)：二叉树的链式存储结构是用一个链表来存储一颗二叉树，二叉树中每一个结点用链表的一个链结点来存储。在二叉树中，结点结构通常包括若干数据域及若干个指针域，在二叉链表中至少包括三个域：
  
  

遍历：

• 先序遍历：先访问根结点，其次遍历左子树，最后遍历右子树。以图1为例，结果为：521387。
• 中序遍历：先遍历左子树，其次访问根结点，最后遍历右子树。以图1为例，结果为：123578。注意结果为有序的，但只满足二叉搜索树，后面会介绍。
• 后序遍历：先遍历左子树，其次遍历右子树，最后访问根结点。以图1为例，结果为：132785。

 注意，对于中序遍历，有如下术语：

• 前驱结点：对二叉树的中序遍历，遍历后的顺序，当前结点的前一个结点为该结点的前驱结点。
• 后继结点：对二叉树的中序遍历，遍历后的顺序，当前结点的后一个结点为该结点的后继结点。

3. 满二叉树

  如下图：

图2：   图2就是一个满二叉树，对比普通的二叉树，它有什么特点？

  不用说，二叉树的特点它都有，那么至于它为什么叫满二叉树，就是因为它的每一个结点，除了叶子结点都有两个子结点，并且每一层都满足最多的子结点数(每一层都填满)。像这种树就叫满二叉树。同时因为每一层都要填满，所以所有的叶子结点都在最下一层。最后注意满二叉树的每个结点的度要么是0，要么是2，不能为1。

4. 完全二叉树

  如下图：

图3： 特点：

• 完全二叉树就是指除了最后一层之外，其它每一层的结点数都是满的。
• 对任意一结点，如果其右子树的最大层次为L，则其左子树的最大层次为L或L+1(子树必须向左对齐，右子树不能单独存在，也就是说，必须先左子树，再右子树。或者说，最后一层的结点是自左向右依次排序的)。
  

图4：

  以上就不属于完全二叉树。因为元素0027是元素0026的右子树，而右子树是不能独立存在的，如果把元素0027换成左子树就可以。

• 度为1的结点只有0或1个。

5. 二叉堆

  二叉堆在完全二叉树的基础之上，增加了节点取值的限制条件，分为两种堆，最大堆和最小堆。

• 最大堆：各个父结点的值总是大于或等于任何一个子结点的值。
• 最小堆：各个父结点的值总是小于或等于任何一个子结点的值。

如下就是最小堆：

图5：

  看根结点0，它有两个子结点分别是1和3，根据最小堆的概念，0是不是小于1和3？是不是满足条件，然后再继续看元素为1的结点，它也一样有两个子结点为4和2，根据概念，1是不是小于4和2？依次类推，只要全部满足那么这颗树就是二叉堆。

6. 二叉搜索树

  二叉搜索树又叫二叉查找树或二叉排序树，是一颗特殊的二叉树，那么要成为一颗二叉树要满足哪些条件？如下：

• 左子树不空，则左子树所有结点值均小于或等于该结点的值。
• 右子树不空，则左子树所有结点值均大于或等于该结点的值。
• 左右子树也是二叉搜索树。

  说白了就是一个结点它的左子树是小于或等于它的，而它的右子树是大于或等于它的。
  还记得中序遍历吧，只有二叉搜索树进行中序遍历的结果才是有序的，也就是说，图1就是一个二叉搜索树。
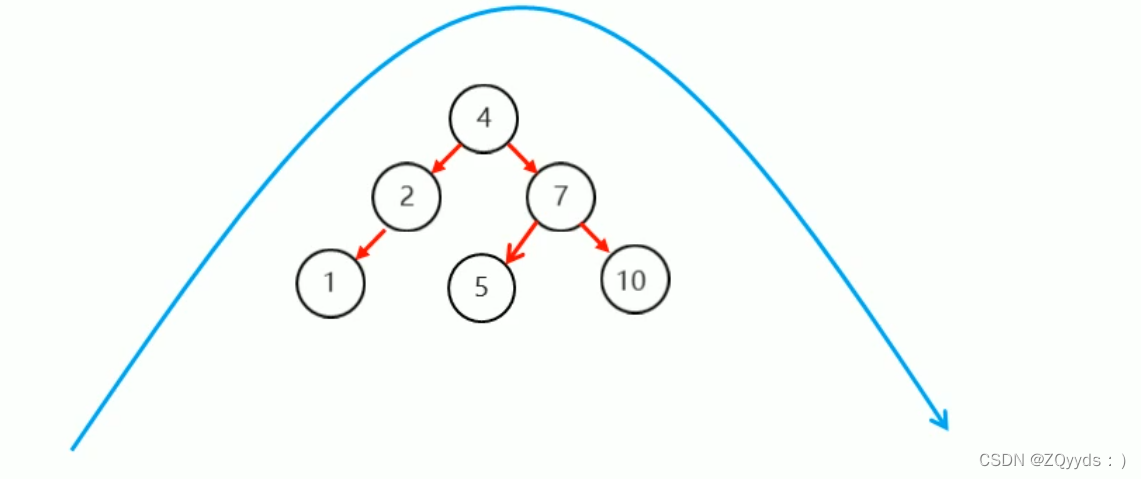
  比如有这么一行数，为256174，那么我们怎么用二叉搜索树来存储呢？如下：

图6：

  你还可以对上图进行中序排序，看看是不是124567。结果就是有序的。
  所以假如有这么一行数据，1234567，缺点是不是暴露出来了呀，是不是二叉树就被退化成一个链表呀！那怎么办呀，这就要引入一个平衡二叉树了。

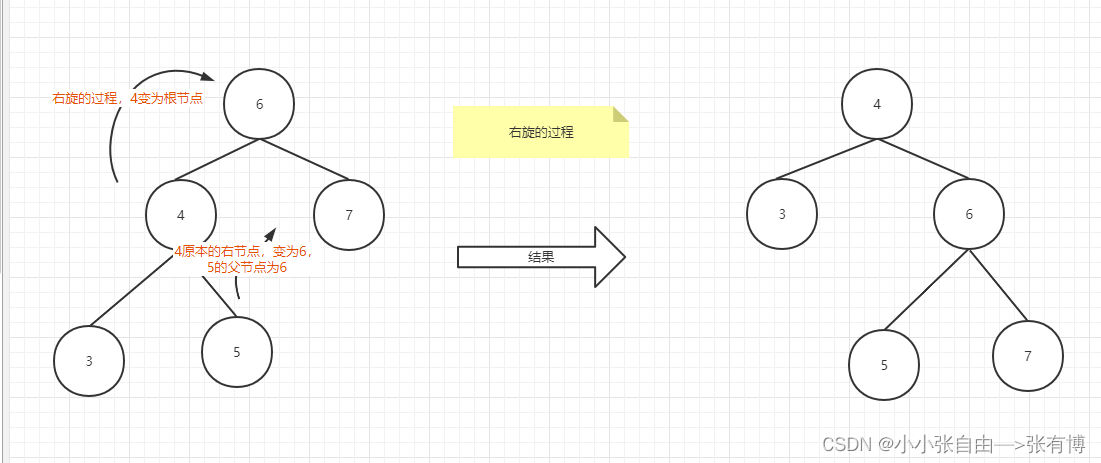
左旋和右旋

7. 平衡二叉树(平衡二叉搜索树)

  平衡二叉树又称为AVL树，于1962年首次提出。有如下特点：

• 左右子树深度之差的绝对值不超过1。最高层-最底层<=1，所以平衡二叉树只是相对平衡。
• 左右子树仍然为平衡二叉树。

  衡量是否为平衡二叉树，引入一个概念，平衡因子：定义结点左子树与右子树的高度差为该结点的平衡因子，平衡因子的值只可能是-1(右子树比左子树高1),0(一样高),1(左子树比右子树高1)。如果不是这3个数，比如2，那就说明你这颗树不平衡了。如下图：

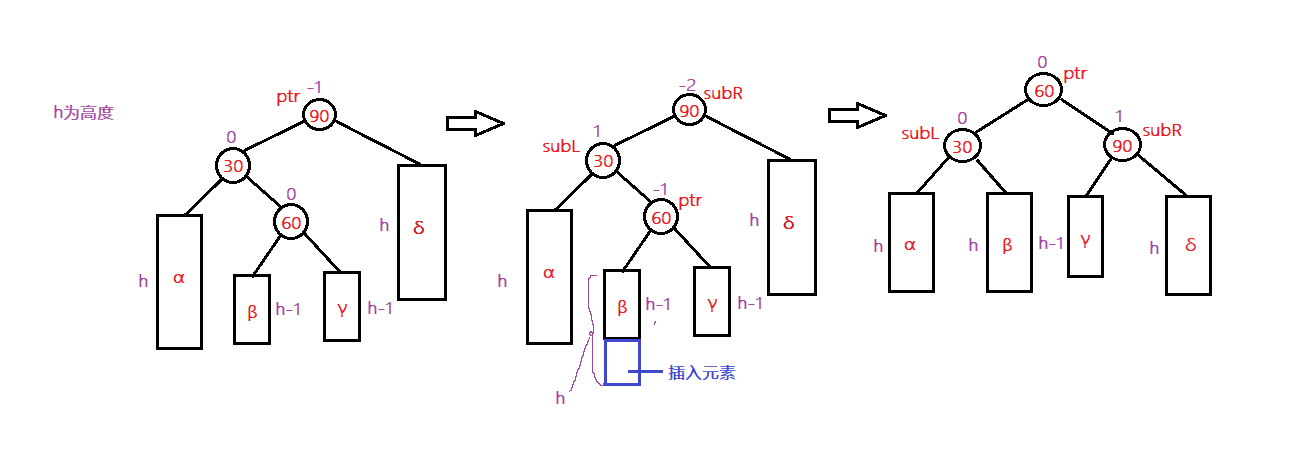
图7：   图7每个结点要么是0，要么是-1或1，并不存在大于1的或小于-1的情况，所以图7这颗树就是平衡二叉搜索树。那么非平衡的例子就是图6了，为什么图6非平衡呢？如下：   那问题来了，如何解决这个问题呢？要解决这个问题就要涉及到旋转的知识了，这个知识点我也是花了两个小时才琢磨出来它是怎么转的，其实很简单。首先要知道有如下四种情况，如下：

  也就是说，遇到问题，首先要分析它是上图中的哪一种情况，因为到时候调整会有左旋右旋之分，包括调整次数，我说明一下，上图LL和RR只需要调整一次，而LR和RL要调整两次才平衡。那么好，我们就对图6进行调整，首先，看到图6这张图，根据平衡因子计算，它不平衡，要调整，ok，没问题，那怎么调，看，它是上图4种的哪一种？怎么看？比如图6，是怎么导致不平衡的，你是不是要找出来，谁？是不是元素7的加入导致树的不平衡？你可以把元素7干掉，是不是就是平衡树，那么我们是不是找到罪魁祸首了呀，那么好，根据我上图说的4种情况的概念出发，它是不是属于RR情况，你读呗，括号里我是不是写了当根节点右子树的右子树有节点插入，导致二叉树不平衡。所以明白了吧，而且我也说了，RR只需要调整一次即可平衡，所谓的调整就是你要么左旋要么右旋，那么到底是左旋还是右旋呢？你可以想一下天平秤，如下：
  你就把中间的那个分度盘看作是根结点，横梁的两边就分别是左子树和右子树，你看上图。右边的那个横梁是不是往下跑了呀，是不是就说明了右边的东西重一点，那么为了保持平衡，你是不是下意识的会用你的手去拖你右边的那个托盘往上托，让它跟左边的横梁保持在一条直线上，是不是？那就没问题了，我们现在要解的这道题，就跟图上那个天平秤一样，往上托，也就是逆时针，准确讲就是左旋，是不是so easy。所以如下：
  图画的有点丑啊，没关系，将就的看吧。好，回到正题，也就是说以根节点(分度盘)为圆形，右子树往上托，那么就会造成右子树的根结点成为整个树的根结点，原来的根结点就会沦为小弟成为右子树的根结点的左子树，既然原来的根结点都沦为给别人当小弟了，那么大哥是不是要表示表示，那么大哥就会把它原来的左子树也就是上图中的元素4给元素2，成为它的右子树，所以上图我们是不是要改造一下呀，不然就不叫二叉，直接叫三叉吧，如下：
  这样不就平衡了吗？是不是简单易懂，那么相应的，LL调整就是反过来的，什么旋，右旋，这我就不说了，看第二种情况，如下：
  别冲动，别一看到右边的多，就着急往上托，要先分析，它属于上述4种情况的哪一种情况？我们先看上图，为了保持平衡我们是不是得把元素8的结点给坎了呀，所以，再结合4种情况的每一个概念分析，比如先从根结点出发，然后走右子树，再走右子树的左子树，那么你明白了吗，是不是就是RL调整呀，而且我还说了，只要是RL或LR就要经历两次调整，也就是两次旋转，你能像第一种情况那样直接就左旋吗，肯定不行，不信你试试，在草稿纸上画一画，我就懒得在电脑上画一遍了。那怎么搞？首先，问题是不是出在右子树上？那么我们就只针对右子树，也就是如下：
  那么我们就要对它采用右旋，如下：
  这是不是做了一次调整呀，然后再结合剩下的两个元素，如下：
  不过这样还没有平衡哦，还是一样分析是哪一种情况，再做最后一次调整就行了，经过分析，它属于RR调整这个情况，所以右子树整体往上移，怎么移，说过了，要是不会移就说明我的第一种情况你没看懂。
  最后注意，以上几种情况是边添加数据边调整的。

注意(后期整理)：
  在后面重新查看的时候，发现少说了一点，就是最小平衡因子，所以这里补上，有如下图：
  如上图，罪魁祸首就是元素5的加入导致的不平衡，没问题，但还有一个问题，图上有两个结点也就是元素2和3它们的平衡因子都是-2，也就是出现了两个不平衡的因子，那听谁的？结果应该是听元素3的，因为所谓的最小平衡因子就是找离罪魁祸首(元素5)最近的不平衡元素，是不是元素3呀，元素3是不是离元素5近，所以，我们在调整的时候就应该调整以元素3为根节点的子树，也就是如下：
  再结合剩下的两个元素1和2，最终结果如下：