一、树的演变

为什么会有树，因为链表的查询效率是logOn,树的查询效率是Log2n。

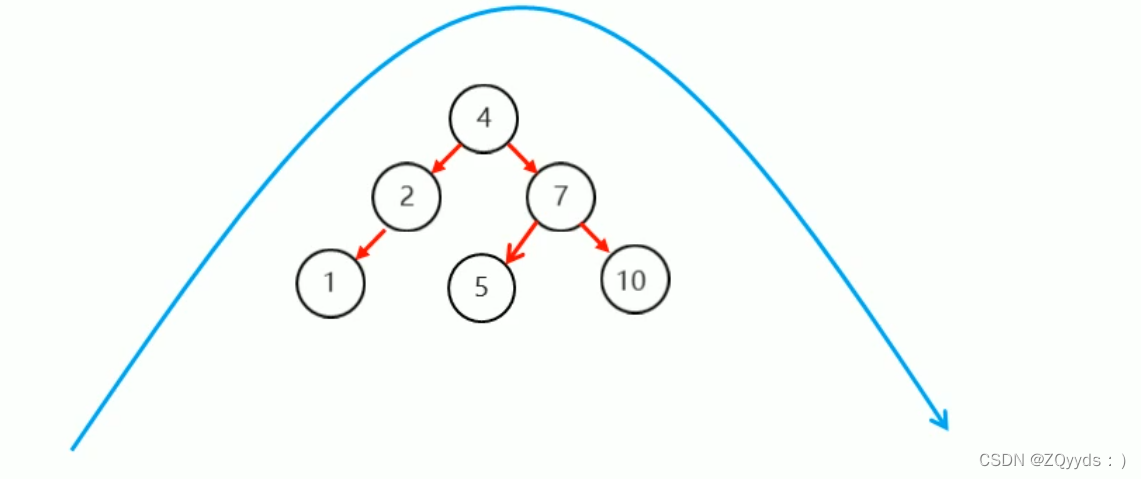
为什么会有二叉搜索树，在查找某个值的时候，一共就只有三种结果，大于，小于，等于，根据这三种情况并设计出了二叉查找树，为了方便检索。

为什么会有平衡二叉搜索树（AVL），因为二叉搜索树会退化成一个链表。变成单支树

为什么会后红黑树，因为AVL树在插入或者删除数据的时候，为了保证树结构的严格的平衡性，就需要经常的去调整树的结构，所以插入数据的效率是比较低的，反之获取数据的效率比较高。红黑树结构上比较平衡，对平衡的要求确没有自平衡二叉搜索树那么高

红黑树平衡的代价较低，其平均统计性能要强于 AVL

二、红黑树

1.红黑树的特点

性质1. 结点是红色或黑色。

性质2. 根结点是黑色。

性质3. 所有叶子都是黑色。（叶子是NIL结点）

性质4. 每个红色结点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色结点）

性质5. 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。（黑色是平衡的）

总结红黑树是特殊点AVL树，黑根黑叶红不邻，同祖等高只数黑

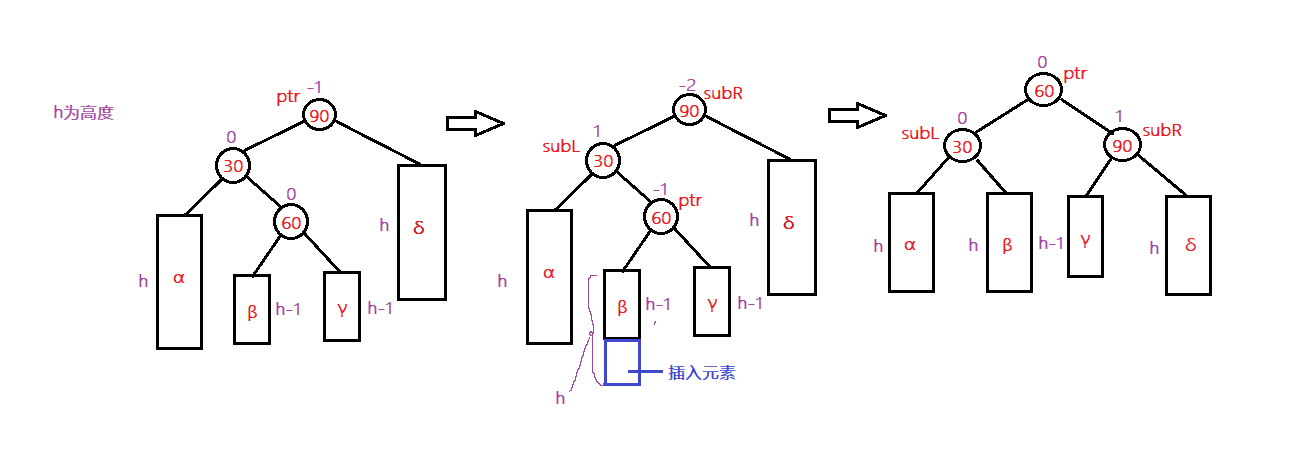
2.树左旋右旋的过程

左旋：

右旋：左旋的逆过程

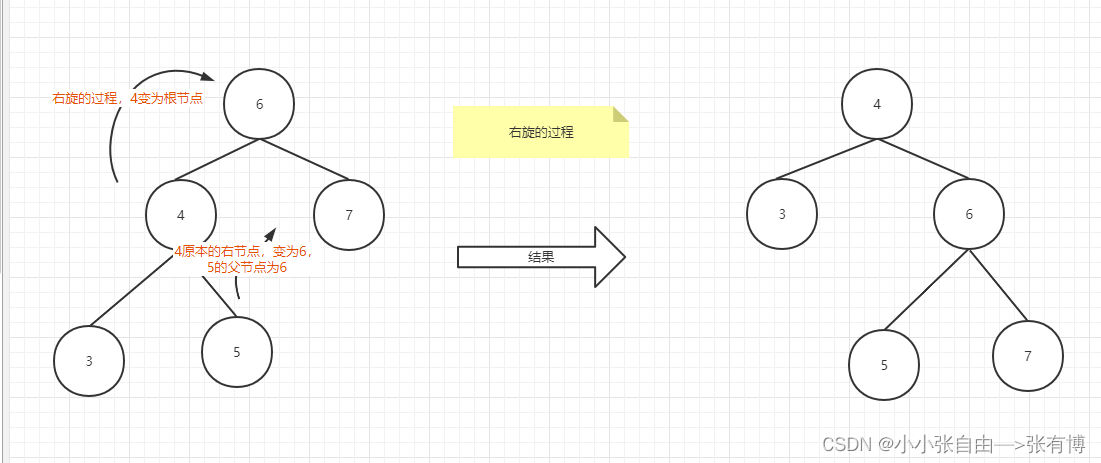
3.红黑树插入节点情景分析：

数据结构学习之树与红黑树（java1.8 hashMap底层实现）_倔强的耗子的博客-CSDN博客

三、HashMap插入平衡、左旋、右旋源码解析

putval():添加值

resize():扩容

treeifyBin():树化,节点变为TreeNode

//插入平衡，左旋，右旋的过程其实就是染色（赋值）+改变节点的指针

balanceInsertion():插入平衡

rotateLeft() :左旋

rotateRight ：右旋

1.添加值

 //执行 put() public V put(K key, V value) {//key = "java" value = PRESENT 共享return putVal(hash(key), key, value, false, true);}//执行 putVal
final V putVal ( int hash, K key, V value,boolean onlyIfAbsent,boolean evict){Node<K, V>[] tab; Node<K, V> p;int n, i; //定义了辅助变量//table 就是 HashMap 的一个数组，类型是 Node[]//if 语句表示如果当前 table 是 null, 或者 大小=0//就是第一次扩容，到 16 个空间.if ((tab = table) == null || (n = tab.length) == 0)n = (tab = resize()).length;//如果 p 为 null, 表示还没有存放元素,创建Node对象，插入if ((p = tab[i = (n - 1) & hash]) == null)tab[i] = newNode(hash, key, value, null);else {Node<K,V> e; K k; ////如果当前索引位置有值，就覆盖if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k))))e = p;//如果是一颗红黑树，就调用 putTreeVal , 来进行添加else if (p instanceof TreeNode)e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);else {//此时 table 对应索引位置，已经是一个链表, 就使用 for 循环比较for (int binCount = 0; ; ++binCount) {if ((e = p.next) == null) {p.next = newNode(hash, key, value, null); //元素添加到链表后//该链表是否已经达到 8 个结点if (binCount >= TREEIFY_THRESHOLD(8) - 1) treeifyBin(tab, hash); //树化break;}if (e.hash == hash &&((k = e.key) == key || (key != null && key.equals(k))))break;p = e;}}if(e !=null)   {// existing mapping for key V oldValue = e.value;if (!onlyIfAbsent || oldValue == null)e.value = value;afterNodeAccess(e);return oldValue;}}++modCount;//size 就是我们每加入一个结点 Node(k,v,h,next), size++if (++size > threshold)resize();//扩容afterNodeInsertion(evict);return null;}

2.插入平衡


/*** 插入平衡（分多钟情况，左旋，右旋）* @param root 当前根节点* @param x 当前要插入的节点* @return  返回根节点(平衡涉及左旋右旋会将根节点改变，所以需要返回最新的根节点) */
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,TreeNode<K,V> x) {x.red = true; //首先将要插入的节点染色成红色，不要问为什么不是黑色，因为黑色会破坏黑高(黑色完美平衡)		     //xp:x的父节点,xpp:x的爷爷节点，xppl:爷爷节点的左子节点，xppr:爷爷节点的右子节点for (TreeNode<K,V> xp, xpp, xppl, xppr;;) { //死循环，直到找到根节点才结束。if ((xp = x.parent) == null) { //如果当前插入节点的父节点为空，那么说明当前节点就是根节点，x.red = false;	//染色为黑色（根节点规定为黑色）return x;}else if (!xp.red || (xpp = xp.parent) == null) //如果爸爸节点为黑色或者爷爷节点为空（插入后不影响黑色完美平衡，直接返回）return root;if (xp == (xppl = xpp.left)) { //当前插入节点的父节点为红色，并且是爷爷节点的左子节点（有两种情况：LL或者LR）if ((xppr = xpp.right) != null && xppr.red) { //叔叔节点存在并且为红色 xppr.red = false; //将爸爸节点和叔叔节点染色成黑xp.red = false;xpp.red = true; //将爷爷节点染色成红x = xpp; //最后将爷爷节点设置为当前节点进行下一轮操作}else { //叔叔节点不存在或者为黑色if (x == xp.right) { // 当前插入节点是父节点的右子节点（LR的情景）root = rotateLeft(root, x = xp); //以爸爸节点为旋转节点进行左旋xpp = (xp = x.parent) == null ? null : xp.parent; //设置爷爷节点}if (xp != null) { //左旋完了之后，就回到了LL的情景(爸爸节点是爷爷节点的左子节点，当前节点是爸爸节点的左子节点)，然后爸爸节点又是红色，当前插入节点也是红色，违反了红黑色的性质，红色不能两两相连，所以接下来需要进行染色；xp.red = false;  //将爸爸节点染色为黑if (xpp != null) {xpp.red = true; //将爷爷节点染色为红，然后在对爷爷节点右旋。root = rotateRight(root, xpp);}}}}else { //爸爸节点是爷爷节点的右子节点，爸爸节点为红色，也有两种情况（RR 或者 RL）if (xppl != null && xppl.red) { //叔叔节点不为空并且为红色xppl.red = false; //需要将爸爸节点和叔叔节点染色成黑xp.red = false;xpp.red = true; //将爷爷节点染色成红x = xpp; //并且爷爷节点设置为当前节点进行下一轮操作}else { //叔叔节点不存在或者为黑色if (x == xp.left) { //当前插入节点是爸爸节点的左子节点(RL的情景)root = rotateRight(root, x = xp); //先将爸爸节点右旋变成的RR的情景xpp = (xp = x.parent) == null ? null : xp.parent;}if (xp != null) { //这个时候已经变成了RR的情况，需要染色在意爷爷节点左旋来维持平衡xp.red = false; //将爸爸节点染色为黑if (xpp != null) {xpp.red = true; //将爷爷节点染色成红root = rotateLeft(root, xpp); //在对爷爷节点左旋}}}}}}

3.左旋、右旋

/*** 左旋* @param root 当前根节点* @param p 指定的旋转节点* @return  返回根节点(平衡涉及左旋右旋会将根节点改变，所以需要返回最新的根节点) * 左旋示意图：左旋p节点pp                  pp|                   |p                   r/ \         ---->   / \l   r               p   rr/ \             / \rl  rr          l   rl左旋做了几件事？* 1、将rl设置为p的右子节点，将rl的父节点设置为p* 2、将r的父节点设置pp,将pp的左子节点或者右子节点设置为r* 3、将r的左子节点设置为p,将p的父节点设置为r*/
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,TreeNode<K,V> p) {// r：旋转节点的右子节点；	pp:旋转节点的父节点， rl:旋转节点的右子节点的左子节点TreeNode<K,V> r, pp, rl;if (p != null && (r = p.right) != null) { //旋转节点非空并且旋转节点的右子节点非空if ((rl = p.right = r.left) != null)  //将p节点的右子节点设置为右子节点的左子节点rl.parent = p; //将rl的父节点设置为pif ((pp = r.parent = p.parent) == null)//将r的爸爸节点设置为p的爸爸节点，如果是空的话(root = r).red = false;//染色成黑else if (pp.left == p) //判断父节点是爷爷节点的左子节点还是右子节点pp.left = r; //如果是左子节点，那么就把爷爷节点的左子节点设置为relse  pp.right = r; //如果是右子节点，就把爷爷节点的右子节点设置为rr.left = p; //最后将r的左子节点设置为pp.parent = r; //将p的爸爸节点设置为r}return root;}/*** 右旋* @param root 当前根节点* @param p 指定的旋转节点* @return  返回根节点(平衡涉及左旋右旋会将根节点改变，所以需要返回最新的根节点) * 右旋示意图：右旋p节点pp                      pp|                       |p                       l/ \          ---->      / \l   r                   ll  p/ \                         / \ll  lr                      lr  r* 右旋都做了几件事？* 1.将lr设置为p节点的左子节点，将lr的父节点设置为p* 2.将l的父节点设置为pp,将pp的左子节点或者右子节点设置为l* 3.将l的右子节点设置为p,将p的父节点设置为l*/
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,TreeNode<K,V> p) {//l:p节点的左子节点 pp:p节点的爸爸节点 lr:p节点的左子节点的右子节点TreeNode<K,V> l, pp, lr;if (p != null && (l = p.left) != null) { //旋转节点p非空并且p节点的左子节点非空if ((lr = p.left = l.right) != null) //将p节点的左子节点设置为左子节点的右子节点lr.parent = p; //然后将p节点的左子节点的右子节点的父节点设置为pif ((pp = l.parent = p.parent) == null) //将p节点的左子节点的父节点设置为p的父节点，如果为空的话，说明l就是根节点了(root = l).red = false; //染色成黑else if (pp.right == p) //判断p节点是pp节点的左子节点还是右子节点，pp.right = l; //如果p节点是pp节点的右子节点的话，将爸爸节点pp的右子节点设置为lelse //如果p节点是pp节点的左子节点的话，将爸爸节点pp的左子节点设置为lpp.left = l;l.right = p; //最后将l节点的右子节点设置为pp.parent = l; //将p节点的父节点设置为l}return root;}