平衡二叉查找树（AVL）的构建—

平衡二叉查找树（AVL）的构建——左旋右旋

article/2025/9/29 15:26:55

原文链接：https://www.cnblogs.com/ZhaoxiCheung/p/6012783.html

平衡二叉树，又称AVL（Adelson-Velskii和Landis）树，是带有平衡条件的二叉查找树。这个平衡条件必须要容易保持，而且它必须保证树的深度是 O（log N）。

一棵AVL树是其每个节点的左子树和右子树的高度最多差1的二叉查找树（空树的高度定义为 -1 ）。查找、插入和删除在平均和最坏情况下都是 O（log n）。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。

1、LL型（单次右旋转）

k2的左子树比右子树高２，所以不平衡，我们需要把k1提到k2的位置，然后k2下降到k1的右子树，最后还有把k1的右子树放到k2的左子树即可。
在这里插入图片描述

//LL型旋转（单次右旋）
static Position SingleRotateWithLeft( Position K2 )
{Position K1;K1 = K2->Left;          //找到 K2 左子树K2->Left = K1->Right;   //将 K1 右子树移到 K2 的左子树K1->Right = K2;         //建立 K1 和 K2 的关系K2->Height = Max( Height( K2->Left ), Height( K2->Right ) ) + 1;K1->Height = Max( Height( K1->Left ), K2->Height ) + 1;return K1;  /* New root */
}

2、RR型（单次右旋转）

与LL型对称，原理类似
在这里插入图片描述

static Position SingleRotateWithRight( Position K1 )
{Position K2;K2 = K1->Right;K1->Right = K2->Left;K2->Left = K1;K1->Height = Max( Height( K1->Left ), Height( K1->Right ) ) + 1;K2->Height = Max( Height( K2->Right ), K1->Height ) + 1;return K2;  /* New root */
}

3、LR型双旋转（单次左旋后右旋）

先以K3的左子树为根节点执行一次左左旋转，然后以k3的根节点，执行一次右右旋转即可。
在这里插入图片描述

static Position DoubleRotateWithLeft( Position K3 )
{/* Rotate between K1 and K2 */K3->Left = SingleRotateWithRight( K3->Left );/* Rotate between K3 and K2 */return SingleRotateWithLeft( K3 );
}

4、RL型双旋转（单次右旋后单次左旋）

与LR型双旋转对称，原理类似
在这里插入图片描述

static Position DoubleRotateWithRight( Position K1 )
{/* Rotate between K3 and K2 */K1->Right = SingleRotateWithLeft( K1->Right );/* Rotate between K1 and K2 */return SingleRotateWithRight( K1 );
}

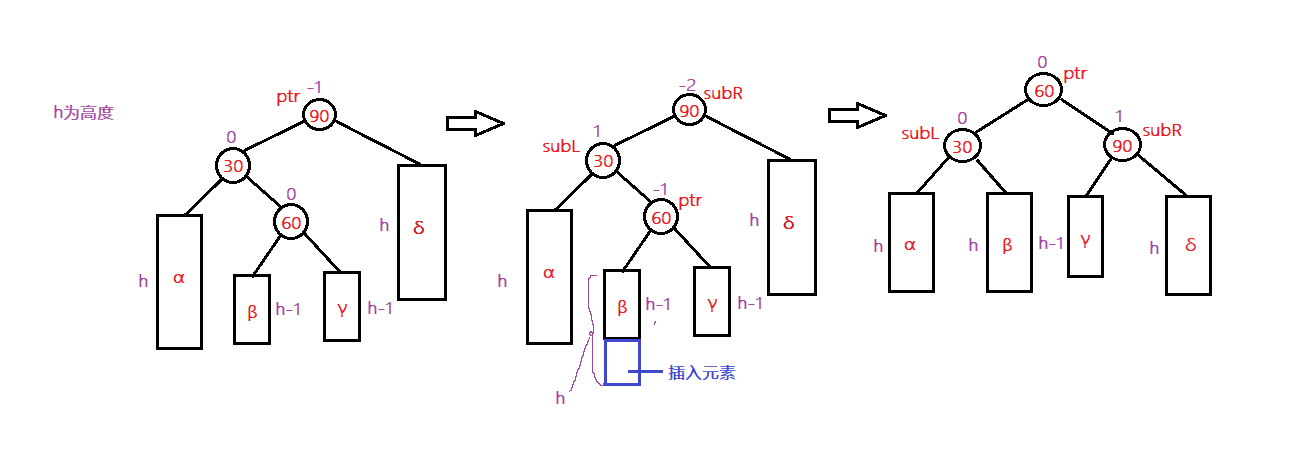
5、结点插入

AVL树进行插入操作时，会破坏二叉树的平衡性，所以每当插入一个数据时，都要从插入点往上，一步一步检测出是否出现平衡因子大于1的，如果有，则要做相应的旋转。

AvlTree Insert( ElementType X, AvlTree T )
{if( T == NULL ){/* Create and return a one-node tree */T = malloc( sizeof( struct AvlNode ) );if( T == NULL )FatalError( "Out of space!!!" );else{T->Element = X;T->Height = 0;T->Left = T->Right = NULL;}}else if( X < T->Element )                              //插入值比当前结点值小，往左子树插入{T->Left = Insert( X, T->Left );                    //递归插入if( Height( T->Left ) - Height( T->Right ) == 2 )  //判断子树是否平衡if( X < T->Left->Element )                     //比当前结点左子树的值小，即为左左情形。T = SingleRotateWithLeft( T );             //LL旋转（右单旋转）else                                           //否则为左右情形T = DoubleRotateWithLeft( T );             //LR旋转}else if( X > T->Element )                              //插入值比当前结点值大，往右子树插入{T->Right = Insert( X, T->Right );                  //递归插入if( Height( T->Right ) - Height( T->Left ) == 2 )  //判断子树是否平衡if( X > T->Right->Element )                    //比当前结点右子树大，即为右右情形T = SingleRotateWithRight( T );            //RR旋转（左单旋转）else                                           //否则为右左情形T = DoubleRotateWithRight( T );            //RL旋转}/* Else X is in the tree already; we'll do nothing */T->Height = Max( Height( T->Left ), Height( T->Right ) ) + 1;return T;
}

6、结点删除

结点删除包括四种情况：

左右子树都非空
左子树为空，右子树非空
右子树为空，左子树非空
左右子树都为空

AvlTree Delete(ElementType X,AvlTree T)
{if (T == NULL)                        //空树直接返回return NULL;if (x < T->Element)                   //删除值小于当前节点，说明删除节点在当前节点左侧{T->Left = Delete(X,T->Left);if (Height(T->Right) - Height(T->Left) == 2){if (Height(T->Right->Left) > Height(T->Right->Right))T = DoubleRotateRL(T);elseT = SingleRotateRight(T);}}else if (X > T->Element)             //删除节点在当前节点右侧{T->Right = Delete(X,T->Right);if (Height(T->Left) - Height(T->Right) == 2){if (Height(T->Left->Right) > Height(T->Left->Left))T = DoubleRotateLR(T);elseT = SingleRotateLeft(T);}}else                                 //找到删除节点{if (T->Right)                    //右子树不为空的情况{AvlTree tmp = T->Right;while (tmp->Left != NULL) tmp = tmp->Left;  //找到要删除的结点的右子树的左子树最小值，以便替要删除的结点T->Element = tmp->Element;T->height = tmp->height;T->Right = Delete(tmp->Element,T->Right); //递归删除}else{//右子树为空的情况，free节点，返回被删除节点的左节点//这也是真正删除节点的地方AvlTree tmp=T;T = T->Left;free(emp);return T;}}//每次删除之后，都要更新节点的高度T->height = Max(Height(T->Left),Height(T->Right)) + 1;return T;
}