图示讲解AVL平衡二叉树的左旋和右旋

article/2025/9/28 21:58:37

AVLTree

高度平衡的搜索二叉树
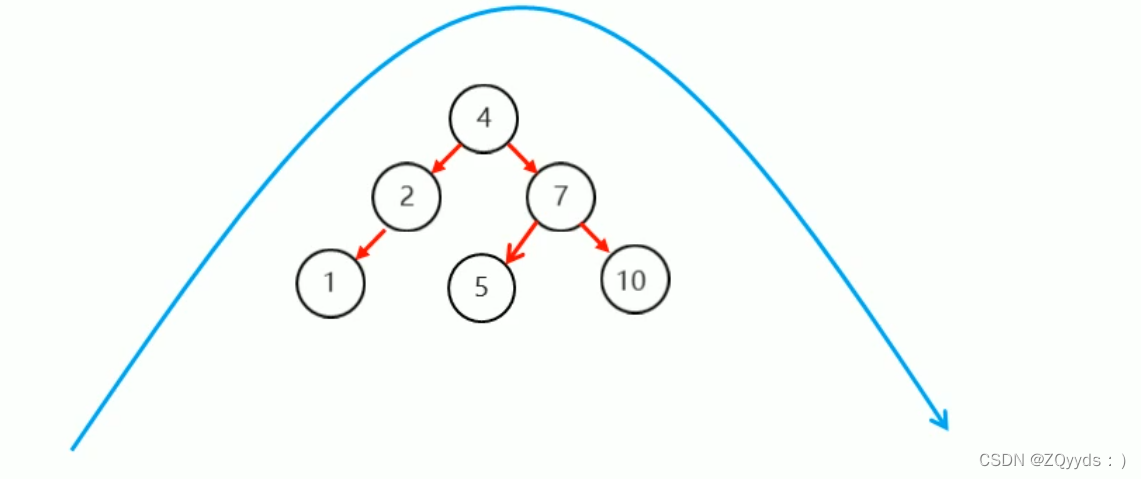
一棵平衡树，或是空树，或是具有以下性质的二叉搜索树：左子树和右子树都是AVL树，且左右子树的高度之差的绝对值不超过1。
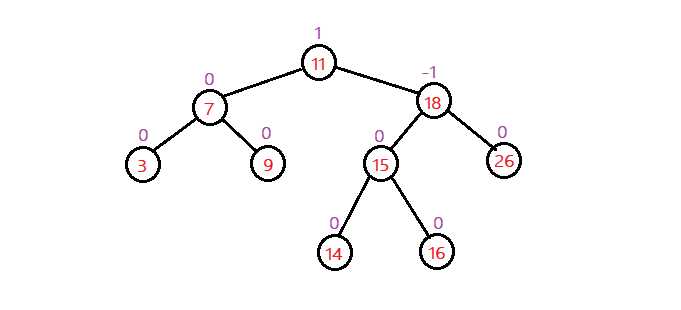
这里写图片描述
该二叉树，根结点的右子树高度为3，左子树高度为2。结点上方的数字为平衡因子，因为右子树高度比左子树高度大1，所以根结点的平衡因子为1。
一颗平衡二叉树，如果有n个结点，其高度可保持O(log2^n),平均搜索长度也可以保持在O(log2^n)

平衡化旋转

AVL树相较于普通的二叉搜索树，自主要的就是做了平衡化处理，使得二叉树变的平衡，高度降低。
在插入一个结点后应该沿搜索路径将路径上的结点平衡因子进行修改，当平衡因子大于1时，就需要进行平衡化处理。从发生不平衡的结点起，沿刚才回溯的路径取直接下两层的结点，如果这三个结点在一条直线上，则采用单旋转进行平衡化，如果这三个结点位于一条折线上，则采用双旋转进行平衡化。

单旋转

左单旋

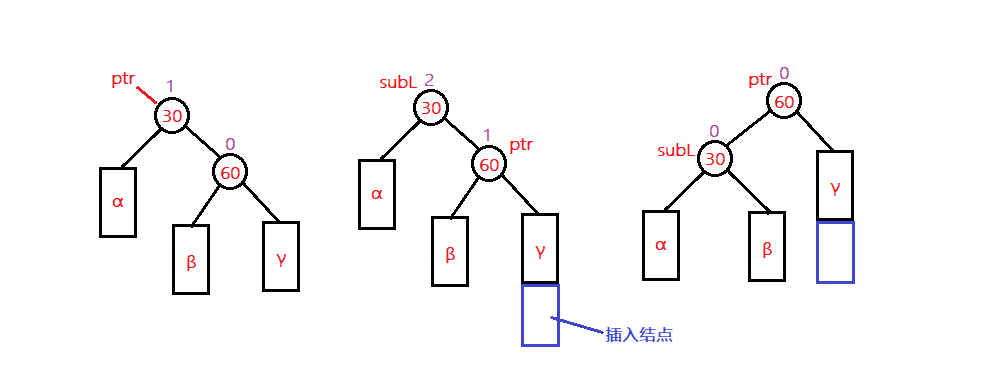
这里写图片描述
动图演示，图片内容可以无视，看懂操作进行了
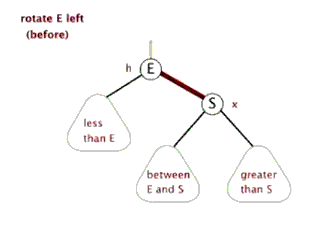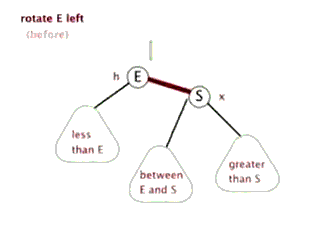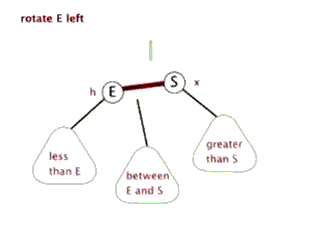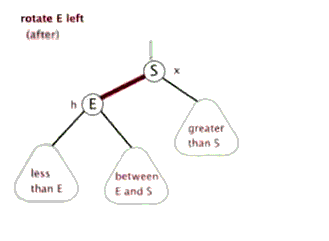
这里写图片描述
将右子树的左子树链接到父亲节点的右孩子结点，父亲节点作为ptr结点的左孩子结点便完成了旋转。

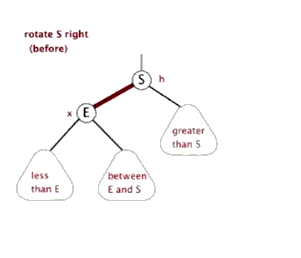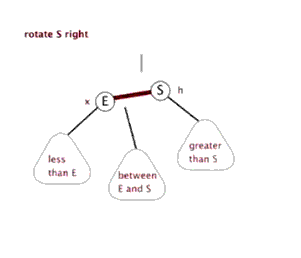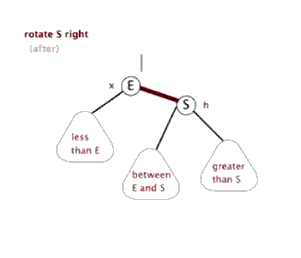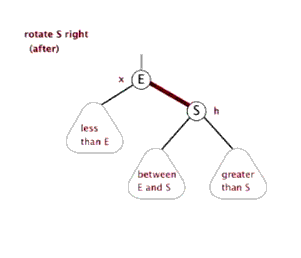
右单旋

右单旋是左单旋的镜像旋转.
当前节点ptr，与父亲节点和当前节点的左孩子结点位于一条直线上时，使用右单旋进行平衡。
这里写图片描述

双旋转

先左后右双旋转

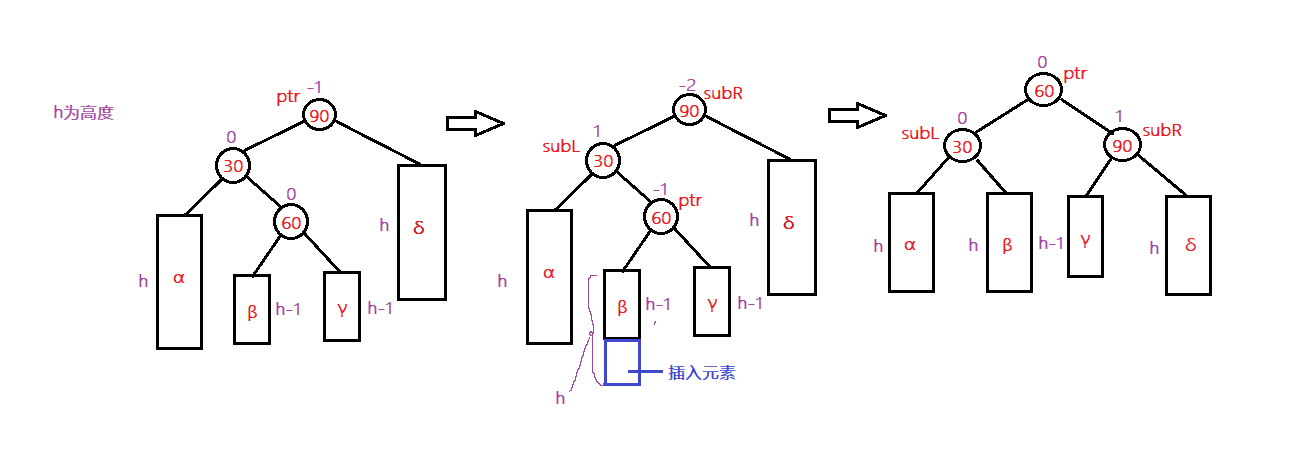
这里写图片描述
当在ptr的左子树的右子树中插入一个结点后，造成了ptr平衡因子为-2的不平衡，将ptr向下找到当前结点的左孩子的右孩子，先进行左单旋ptr->left = subL，然后将ptr的右子树断开指向subR，此时便完成了旋转，最后将平衡因子进行更新。

先右后左双旋转

先右单旋再左单旋，是先左后右的镜像旋转，这里就不做赘述了。

代码实现

#include<stack>
#include<iostream>
using namespace std;template<class K,class V>
struct AVLNode
{AVLNode<K, V> * _pLeft;AVLNode<K, V> * _pRight;K key;V value;int bf;AVLNode():_pLeft(NULL), _pRight(NULL){}AVLNode(const K key, const V value):_pLeft(NULL), _pRight(NULL), key(key), value(value), bf(0){}};template<class K,class V>
class AVLTree
{//typedef AVLNode<class K, class V> Node;//typedef AVLNode<class K, class V> * PNode;public:// 构造函数--无参AVLTree():_pRoot(NULL){}构造函函数--含参//AVLTree(const K key, const V value)//{}// 插入函数bool Insert(const K key, const V value){return _Insert(key, value, _pRoot);}// 显示函数void showTree(){_showTree(_pRoot);}// 删除函数bool Remove(K key){return Remove(_pRoot, key);}private:AVLNode<K, V> * _pRoot;// 插入函数bool _Insert(const K key, const V value, AVLNode<K, V> *& ptr){AVLNode<K, V> * pCur = ptr;AVLNode<K, V> *& pParent = _pRoot; // ???????????????????????????????????????????stack<AVLNode<K, V> *> s;while (pCur != NULL){if (pCur->key == key)return false;pParent = pCur;s.push(pParent);if (pCur->key > key){pCur = pCur->_pLeft;}else if (pCur->key < key){pCur = pCur->_pRight;}}// 所插位置为NULL 新建结点pCur = new AVLNode<K, V>(key, value);if (pCur == NULL){cerr << "存储空间不足！" << endl;exit(1);}// 判断是否为空树if (pParent == NULL){ptr = pCur;return true;}if (key < pParent->key)pParent->_pLeft = pCur;elsepParent->_pRight = pCur;// 调整平衡while (s.empty() == false){pParent = s.top();s.pop();if (pCur == pParent->_pLeft)pParent->bf--;elsepParent->bf++;if (pParent->bf == 0)break;if (pParent->bf == 1 || pParent->bf == -1)pCur = pParent;if (pParent->bf == 2 || pParent->bf == -2){// 进行调整int d;// 调整平衡因子d = (pParent->bf < 0) ? -1 : 1;if (pCur->bf == d){if (d == -1)RotateR(pParent); // 右单旋elseRotateL(pParent); // 左单旋}else{if (d == -1)RotateLR(pParent); // 左右双旋elseRotateRL(pParent); // 右左双旋}break;}if (s.empty() == true)pCur = pParent;else{AVLNode<K, V> * q;q = s.top();if (q->key > pParent->key)q->_pLeft = pParent;elseq->_pRight = pParent;}}return true;}// 左单旋void RotateL(AVLNode<K, V> *& ptr){// 右子树比左子树高// 对以ptr为根的AVL树做左单旋转，旋转后新根在ptrAVLNode<K, V> * subL = ptr; // 要左旋的结点ptr = subL->_pRight;subL->_pRight = ptr->_pLeft;ptr->_pLeft = subL;ptr->bf = subL->bf = 0;}// 右单旋void RotateR(AVLNode<K, V> *& ptr){// 左子树比右子树高AVLNode<K, V> * subR = ptr; // 要右旋的结点ptr = ptr->_pLeft;subR->_pLeft = ptr->_pRight;ptr->_pRight = subR;ptr->bf = subR->bf = 0;}// 先左再右单旋void RotateLR(AVLNode<K, V> *& ptr){AVLNode<K, V> * subL = ptr->_pLeft;AVLNode<K, V> * subR = ptr;ptr = subL->_pRight;subL->_pRight = ptr->_pLeft;ptr->_pLeft = subL;if (ptr->bf < 0){subL->bf = 0;}elsesubL->bf = -1;subR->_pLeft = ptr->_pRight;ptr->_pRight = subR;if (ptr->bf == -1)subR->bf = 1;elsesubR->bf = 0;ptr->bf = 0;}// 先右后左旋转void RotateRL(AVLNode<K, V> *& ptr){AVLNode<K, V> * subL = ptr;AVLNode<K, V> * subR = ptr->_pRight;ptr = ptr->_pLeft;subR->_pLeft = ptr->_pRight;ptr->_pRight = subR;if (ptr->bf >= 0)subR->bf = 0;elsesubR->bf = 1;subL->_pRight = ptr->_pLeft;ptr->_pLeft = subL;if (ptr->bf == 1)subL->bf = -1;elsesubL->bf = 0;ptr->bf = 0;}// 显示函数void _showTree(AVLNode<K, V> * ptr){if (ptr == NULL)return;_showTree(ptr->_pLeft);cout << ptr->key << " ";_showTree(ptr->_pRight);}// 删除结点bool Remove(AVLNode<K, V> *& ptr, K key){AVLNode<K, V> * pCur = ptr;AVLNode<K, V> * pParent = ptr;AVLNode<K, V> * gParent = NULL;AVLNode<K, V> * q; // 左右子树均存在时，找左子树的右结点stack<AVLNode<K, V> *> s;int pd = 0;int gd = 0;// 找到需要被删除的结点，将路径上的结点记录在栈中while (pCur != NULL){if (key == pCur->key)break;pParent = pCur;s.push(pParent);if (key > pCur->key)pCur = pCur->_pRight;elsepCur = pCur->_pLeft;}if (pCur == NULL)return false;if (pCur->_pLeft != NULL && pCur->_pRight != NULL){pParent = pCur;s.push(pParent);q = pCur->_pLeft;while (q->_pRight != NULL){pParent = q;s.push(pParent);q = q->_pRight;}pCur->key = q->key;pCur = q;}// 被删除结点pCur只有一个子结点if (pCur->_pLeft != NULL)q = pCur->_pLeft;elseq = pCur->_pRight;if (pParent == NULL)ptr = q;else{if (pParent->_pLeft = pCur)pParent->_pLeft = q;elsepParent->_pRight = q;// 重新平衡化while (s.empty() == false){pParent = s.top();s.pop();if (pParent->_pLeft = pCur)pParent->bf++;elsepParent->bf--;if (s.empty() == false){gParent = s.top();gd = (gParent->_pLeft == pParent) ? -1 : 1;}else gd = 0;if (pParent->bf == 1 || pParent->bf == -1)break;if (pParent->_pLeft != 0){if (pParent->bf < 0){pd = -1;pCur = pParent->_pLeft;}else{pd = 1;pCur = pParent->_pRight;}if (pCur->bf == 0){if (pd == -1){RotateR(pParent);pParent->bf = 1;pParent->_pLeft->bf = -1;}else{RotateL(pParent);pParent->bf = -1;pParent->_pRight->bf = 1;}break;}if (q->bf == pd){if (pd == -1)RotateR(pParent);elseRotateL(pParent);}else{if (pd == -1)RotateLR(pParent);elseRotateRL(pParent);}if (gd == -1)gParent->_pLeft = pParent;else if (gd == 1)gParent->_pRight = pParent;}q = pParent;}if (s.empty() == true)ptr = pParent;}delete pCur;return true;}
};int main()
{AVLTree<int, int> t;t.Insert(1, 11);t.Insert(2, 12);t.Insert(3, 13);t.Insert(4, 14);t.showTree();t.Remove(2);return 0;
}

http://chatgpt.dhexx.cn/article/L91Wur5F.shtml

相关文章

左右旋对比

左右旋对比

目录 前言 一&#xff0c;逆置法 1.1逆置思路 1.2逆置实现 二&#xff0c;左旋和右旋对比 右旋代码分析 特点对比 前言 之前在up主的博客里面已经有过了对于左旋的三种实现方法。当然&#xff0c;如果我们考虑到时间复杂度的问题&#xff0c;那么我们只要一种方法&#xf…
阅读更多...
平衡二叉树的左旋右旋详解 看不懂你打我

平衡二叉树的左旋右旋详解 看不懂你打我

平衡二叉树的左旋右旋 看不懂你打我 左旋右旋的操作为什么要左旋右旋左旋右旋能保持排序二叉排序树的性质吗下次写平衡二叉树的LL、RR、LR、RL。 左旋右旋的操作 1.左旋&#xff1a;对X节点左旋&#xff0c;即以X的右孩子Y为轴&#xff0c;将X节点转下来&#xff0c;变为Y的左…
阅读更多...
二叉树的旋转，左旋和右旋

二叉树的旋转，左旋和右旋

在AVLTree中经常会有以某个节点为点对子树进行旋转的操作&#xff0c;今天就和大家分享一下什么是二叉树的旋转。 这是一棵二叉树&#xff0c;上图称为图一。 将图一中的树以1为旋转点进行左旋后得到图二&#xff1a; 将图一中的树以1为旋转点进行右旋旋后得到图三&#xff1…
阅读更多...
day062：平衡二叉树——左旋、右旋

day062：平衡二叉树——左旋、右旋

二叉树、平衡二叉树的介绍&#xff1a;day061&#xff1a;二叉树、二叉查找树、平衡二叉树_ZQyyds&#xff1a;&#xff09;的博客-CSDN博客 目录 一、平衡二叉树的左旋 1.为什么要左旋、右旋&#xff1f; 2.什么是左旋&#xff1f; 3.图解 二、平衡二叉树的右旋 1.什么是…
阅读更多...
大型json文件格式化【超简单】

大型json文件格式化【超简单】

问题 遇到了一个很大的JSON文件&#xff08;约4M&#xff09;&#xff0c;想格式化查看&#xff0c;在线json工具会直接崩溃&#xff0c;网上其他同学说的python方法之类的我也都实验失败&#xff0c;但是发现了vs code中一个超强的代码格式化 解决1&#xff08;2019.2.10更…
阅读更多...
vscode 格式化 json文件

vscode 格式化 json文件

1、全选 2、右击
阅读更多...
Unity存档系统——Json格式的文件

Unity存档系统——Json格式的文件

实例场景 点击Save按钮后&#xff0c;查看保存的文件 点击Load按钮后加载文档数据 Json介绍https://www.json.org/json-zh.htmlUnity中自带的JsonUtility可以将可序列化对象与Json格式相互转换。 将对象转为可序列化对象需要添加[SerializeField]&#xff0c;且为public&#…
阅读更多...
将json文件格式转化成Excel表格形式

将json文件格式转化成Excel表格形式

在程序员的工作中&#xff0c;经常有产品或者运营部门的小姐姐需要数据&#xff0c;由于不懂技术&#xff0c;就需要我们将Json格式的数据转换成Excel文档提供给她们进行数据分析。 本文就介绍一个非常简单方便的方法 1.运用的是Excel表格自带的功能 首先打开Excel文件 点击插…
阅读更多...
js导出JSON格式文件

js导出JSON格式文件

在src目录下新建tools文件价&#xff0c;在tools文件中新建index.js(文件内名字随意) 在index.js文件中 const Tools {// 导出文件exportJson(name, data) {let blob new Blob([data]); // 创建 blob 对象let link document.createElement("a");link.href URL.…
阅读更多...
json文件

json文件

认识一下 json文件 直接使用记事本打开&#xff1a;例如猫狗二分类 一般都使用类似字典的方式存储&#xff0c;但和字典不同&#xff0c;无论是键还是值&#xff0c;都要加上双引号。 json文件的读取与写入 import jsondata {"a":"1","b":&q…
阅读更多...
JSON格式校验工具

JSON格式校验工具

经常用ApiPost 和 Postman 测试自己写的接口的话&#xff0c;有时会不小心写错传进去的json对象&#xff0c;我们可以用json格式检验工具去检查一下自己json格式。 在线工具&#xff1a;在线 JSON 工具&#xff0c;JSON 校验/格式化/压缩/工具 - 在线工具-wetools.com微工具
阅读更多...
python文件处理——JSON格式文件

python文件处理——JSON格式文件

python文件处理——JSON格式文件 hello&#xff01;我是wakeyo_J&#xff0c;每天一个konwledge point&#xff0c;一起学python&#xff0c;让技术无限发散。 JSON格式文件 python文件处理——JSON格式文件1. JSON格式1.1 JSON常用的两种结构数据类型1.2 JSON数据与python数据…
阅读更多...
json文件格式详解

json文件格式详解

json文件格式详解 JSON(JavaScript Object Notation) 是一种轻量级的数据交换格式。 易于人阅读和编写。同时也易于机器解析和生成。 它基于JavaScript Programming Language, Standard ECMA-262 3rd Edition - December 1999的一个子集。 JSON采用完全独立于语言的文本格式&a…
阅读更多...
json文件格式转换为png文件格式

json文件格式转换为png文件格式

话不多少&#xff0c;直接上代码&#xff0c;更换源目录和目标目录即可 1、导入库 import cv2 import numpy as np import os import shutil import matplotlib.pyplot as plt 2、设置源目录/输出目录 json_dir G:/json_filedir/ #json文件所在文件夹(注&#xff1a;文…
阅读更多...
Notepad++工具 格式化Json文件格式

Notepad++工具 格式化Json文件格式

简介&#xff1a; Notepad是常用的文件查看工具&#xff0c;在查看json的文件时&#xff0c;如果json文件的格式不符合正常的可视格式&#xff0c;那就需要格式化json文件&#xff0c;使之符合我们的可视化需求。 流程&#xff1a; 首先打开Notepad 打开Plugins 在搜索框中填入…
阅读更多...
JSON 文件存储

JSON 文件存储

&#x1f4cb; 个人简介 &#x1f496; 作者简介&#xff1a;大家好&#xff0c;我是W_chuanqi&#xff0c;一个编程爱好者 &#x1f4d9; 个人主页&#xff1a;W_chaunqi &#x1f600; 支持我&#xff1a;点赞&#x1f44d;收藏⭐️留言&#x1f4dd; &#x1f4ac; 愿你我共…
阅读更多...
JSON 文件格式

JSON 文件格式

最近的开发中用到了JSON文件&#xff0c;JSON是网络中比较常用的数据交换格式&#xff0c;Google chrome 浏览器的书签文件就采用了JSON格式。 以下是官方网站对JSON的介绍&#xff0c;URL&#xff1a;http://json.org//json-zh.html JSON(JavaScript Object Notation) 是一种…
阅读更多...
json文件格式标准

json文件格式标准

JSON(JavaScript Object Notation) 是一种轻量级的数据交换格式。 易于人阅读和编写。同时也易于机器解析和生成。 它基于JavaScript Programming Language, Standard ECMA-262 3rd Edition – December 1999的一个子集。 JSON采用完全独立于语言的文本格式&#xff0c;但是也使…
阅读更多...
Json文件格式化方法

Json文件格式化方法

1. JSON 是一种存储和交换数据的语法 当数据在浏览器与服务器之间进行交换时&#xff0c;这些数据只能是文本。 JSON 属于文本&#xff0c;并且我们能够把任何 JavaScript 对象转换为 JSON&#xff0c;然后将 JSON 发送到服务器。 我们也能把从服务器接收到的任何 JSON 转换…
阅读更多...
JSON的三种格式

JSON的三种格式

JSON的三种格式 一、 JSON的全称 JSON的全称是JavaScript Object Notation 二、为什么需要JSON JSON有三种格式&#xff0c;每一种写法都和JS中的数据类型很像&#xff0c;可以很轻松的和JS中的数据类型互相转换 三、JSON的三种格式 &#xff08;一&#xff09;、简单值的形式…
阅读更多...
推荐文章

Copyright @ 2022~2023