二叉树旋转
二叉树的旋转主要是应用在AVL树中,当添加一个节点时候导致左右两个子树的高度差不在是-1 , 1 , 0而变成了2 或者-2。此时就需要用到左旋/右旋了。当然左右旋或者有左旋也是基于左旋和右旋的就是顺序不同,理清旋转的顺序就可以直接调用。
简单的图形表示
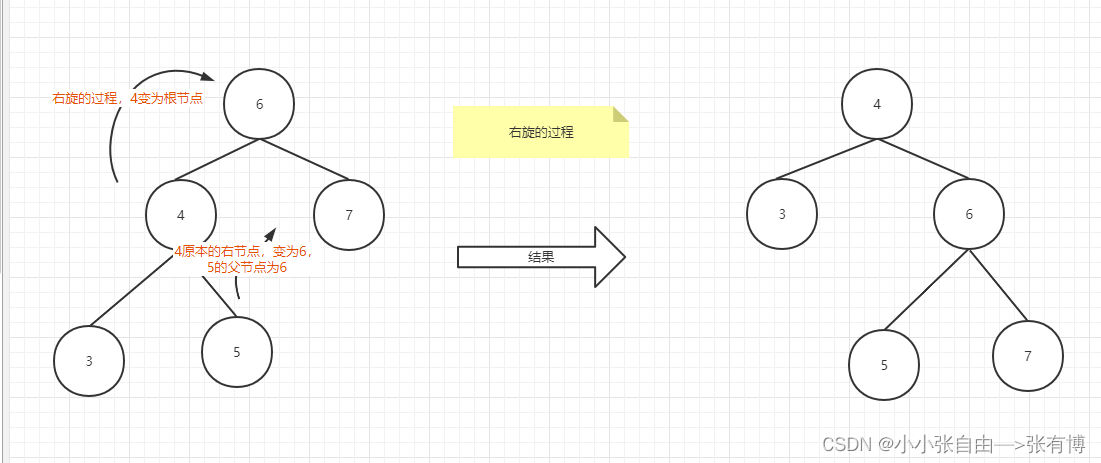
- 右旋

在这里我们加入一个20以后会发现在根节点左右两侧不再满足AVL树了,平衡因子由原来的-1变成了-2,这个时候我们以根节点进行一次右旋操作,即上图中的将40变成当前小树的根节点,50 变成40的右子树,此时我们发现40原本有一个有节点,那么我们就将40这个节点原本的右子树取下来变成50的左子树。此时链接起来,我们发现此时的平衡因子变成0,重新平衡,变成了AVL树,这个就是是右旋。
-
左旋与右旋正好相反,详细步骤可以参考右旋的操作。
-
AVL树的双旋模式
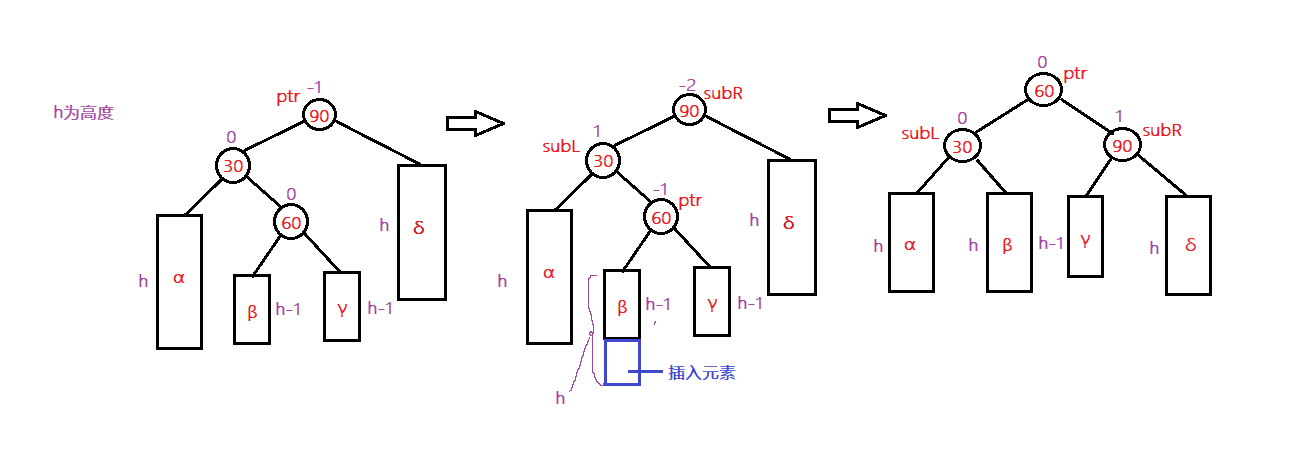
左右旋

根据上图,我们可以看到初始的树在加入一个新的节点40以后,就不在平衡了,(图中标记为绿色的线)。此时我们可以发现单单只有右旋或者左旋是没有办法将它变平衡,所以采用双旋。首先我们可以发现是根节点的左孩子的右子树上多了一个结点,所以我们采用先左旋再右旋的方式将它转换成为平衡结构。先左旋的时候,我们以根节点的左孩子作为旋转的支点,进行旋转。变成图中的第三个的样子,然后再以根节点作为支点进行右旋,最后就平衡了。
右左旋
- 右左旋与左右旋方式相同,但是方向相反,即根节点的右孩子的左子树上多了一个点,进行先右旋再左旋就可以了。
代码实现
存储结构
typedef struct Node
{ int data;struct Node* pLeft; //定义指向左孩子的指针struct Node* pRight; //定义指向右孩子的指针struct Node* pFather; //定义指向父节点的指针
}Tree;右旋
void RightRotate(Tree **p)
{if(*p == NULL || (*p)->pLeft == NULL) return;Tree *pNode = *p;Tree* pMark = (*p)->pLeft;//转换三个孩子的关系pNode->pLeft = pMrk->pRight;pMark->pRight = pNode;//判断父亲是否为空,即判断是否是在根节点进行旋转if(pNode->pFather != NULL){if(pNode == pNode->pFather->pLeft){pNode->pFather->pLeft = pMark;}elsepNode->pFather->pRight = pMark; }else //如果父亲结点空,那么将根节点指向pMark即可{*p = pMark;}//更改变动节点指向的父亲节点if(pNode->pLeft != NULL){pNode->pLeft->pFather = pNode;}pMark->pFather = pNode->pFather;pNode->pFather = pMark;
}左旋
void LeftRotate(Tree** p)
{if(*p == NULL || (*p)->pRight == NULL)return;Tree* pNode = *p;Tree* pMark = (*p)->pRight;//三个孩子的关系pNode->pRight = pMark->pRight;pMark->pLeft = pNode;if(pNode->pFather != NULL){if(pNode == pNode->pFather->pLeft){pNode->pFather->pLeft = pMark;}else {pNode->pFather->pRight = pMark;}}else {*p = pMark;}if(pNode->pRight != NULL){pNode->pRight->pFather = pNode;}pMark->pFather = pNode->pFather;pNode->pFather = pMark;
} 双旋就可以直接调用左旋和右旋进行实现,在这里就不再赘述了。至此,左旋右旋就大致这么多。可能有人看到会问,那怎么判断旋转以后是不是平衡了呢? 其实左旋右旋就像是一个工具,需要的时候就直接调用函数就可以了,简单说就像是一个工具人,用我了我就直接给你来着左旋/右旋。其他的以后想到再进行补充,欢迎大家指出我的错误。