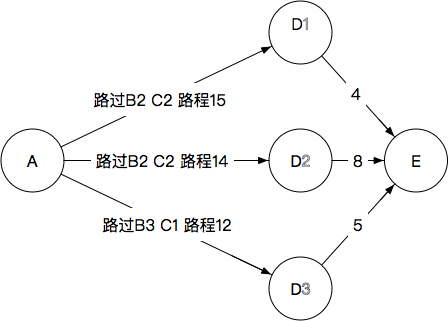
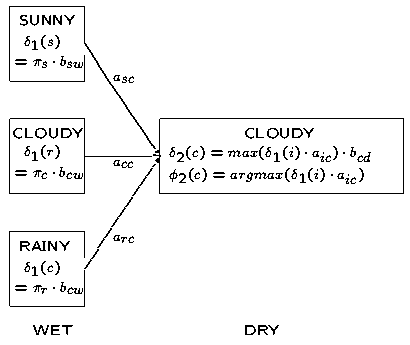
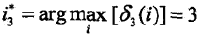viterbi-algorithm 维特比算法的例子解析

article/2025/10/3 22:50:01

维特比算法的目的：

寻找最可能的隐藏状态序列(Finding most probable sequence of hidden states)

关于原理的讲解可以参考下面两篇文章，讲的比较清楚
小白给小白详解维特比算法1.
小白给小白详解维特比算法2.

本文通过分析维特比算法的例子，来学习该算法

  1. 定义HMM的五个重要元素，
# 隐藏序列 S
states = ("Rainy", "Sunny")# 观测序列 K
observations = ('walk', 'shop', 'clean')# 初始概率 π
start_probability = {'Rainy': 0.6, "Sunny": 0.4}# 转移概率 A
transition_probability = {'Rainy': {"Rainy": 0.7, "Sunny": 0.3},"Sunny": {"Rainy": 0.4, "Sunny": 0.6}
}# 发射概率  B
emission_probability = {"Rainy": {"walk": 0.1, "shop": 0.4, "clean": 0.5},"Sunny": {"walk": 0.6, "shop": 0.3, "clean": 0.1},
}

2.定义初始化状态

    # 路径概率表 V[时间][隐状态] = 概率V = [{}]# 一个中间变量，代表当前状态是哪个隐状态path = {}# 初始化初始状态 t=0for y in states:V[0][y] = start_p[y] * emit_p[y][obs[0]]path[y] = [y]

V[时间][天气] = 概率
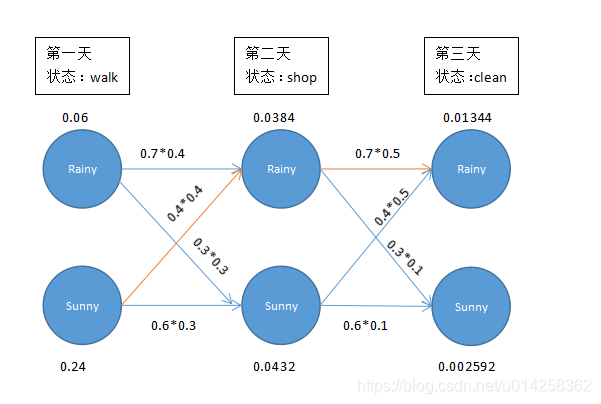
观测序列（observations）得到的结果 观测对象第一天是散步
计算第一天的天气：
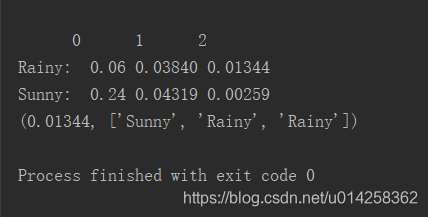
V[第一天][天晴] = 初始概率[天晴] * 发射概率[散步] = 0.4 * 0.6 = 0.24
V[第一天][下雨] = 初始概率[下雨] * 发射概率[散步] = 0.6 * 0.1 = 0.06
计算结果可见，第一天天晴的概率比较大。
此时初始的路径 path = {}

  1. 后面天气的情况都是根据前一天天气概率×转移概率×发射概率得到
def vierbi(obs, states, start_p, trans_p, emit_p):""":param obs:     观察序列    K:param states:  隐藏状态    S:param start_p: 初始概率    π:param trans_p: 转移概率    A:param emit_p:  发射概率    B:return:"""# 路径概率表 V[时间][隐状态] = 概率V = [{}]# 一个中间变量，代表当前状态是哪个隐状态path = {}# 初始化初始状态 t=0for y in states:V[0][y] = start_p[y] * emit_p[y][obs[0]]path[y] = [y]# 对t>0 跑一遍维特比算法for t in range(1, len(obs)):V.append({})newpath = {}for y in states:# 概率 隐状态 =  前状态是y0的概率 * y0转移到y的概率 * y表现为当前状态的概率(prob, state) = max([(V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states])# 记录最大概率V[t][y] = prob# 记录路径newpath[y] = path[state] + [y]# 不需要保存旧路径path = newpathprint_dptable(V)(prob, state) = max([(V[len(obs) - 1][y], y) for y in states])return prob, path[state]

第二天： 由观测序列可得 observations[1] = ‘购物’
① 首先看计算第二天下雨的概率

  • V[第二天][下雨] = V[第一天][下雨] * 转移概率[下雨][下雨] * 发射概率[下雨][购物] = 0.06 * 0.7 * 0.4 = 0.0168
  • V[第二天][下雨] = V[第一天][天晴] * 转移概率[天晴][下雨] * 发射概率[下雨][购物] = 0.24 * 0.4 * 0.4 = 0.0384
    同样在这里取最大概率
    V[第二天][下雨] = 0.0384
    得到的新路径 newpath[下雨] = [晴天，下雨]

②然后计算第二天天晴的概率

  • V[第二天][天晴] = V[第一天][下雨] * 转移概率[下雨][天晴] * 发射概率[天晴][购物] = 0.06 * 0.3 * 0.3 = 0.0054
  • V[第二天][天晴] = V[第一天][天晴] * 转移概率[天晴][天晴] * 发射概率[天晴][购物] = 0.24 * 0.6 * 0.3 = 0.0432
    V[第二天][天晴] = 0.0432
    得到的新路径 newpath[晴天] = [晴天，晴天]

第二天计算完成之后得到前两天的路径
paht={雨天：[晴天，下雨]，晴天:[晴天，晴天]}

以同样的方式得到第三天的结果
observations[1] = 打扫

  • V[第三天][下雨] = V[第二天][下雨] * 转移概率[下雨][下雨] * 发射概率[下雨][打扫] = 0.0384 * 0.7 * 0.5 = 0.01344
  • V[第三天][下雨] = V[第二天][天晴] * 转移概率[天晴][下雨] * 发射概率[下雨][打扫] = 0.0432 * 0.4 * 0.5 = 0.00864
    V[第三天][下雨] = 0.01344
    newpath[下雨] = [晴天，下雨，下雨]
  • V[第三天][天晴] = V[第二天][下雨] * 转移概率[下雨][天晴] * 发射概率[天晴][打扫] = 0.0384* 0.3 * 0.1 = 0.001152
  • V[第三天][天晴] = V[第二天][天晴] * 转移概率[天晴][天晴] * 发射概率[天晴][打扫] = 0.0432 * 0.6 * 0.1 = 0.002592
    V[第三天][天晴] = 0.002592
    newpath[晴天] = [晴天，晴天，晴天]
    把得到的newpath赋值给path

最后通过找出V[第三天]中天气最大的那个概率得到天气的情况
因此第三天的天气为V[第三天][下雨] = 0.01344
由此可反推得到路径path[下雨] = [晴天，下雨，下雨]

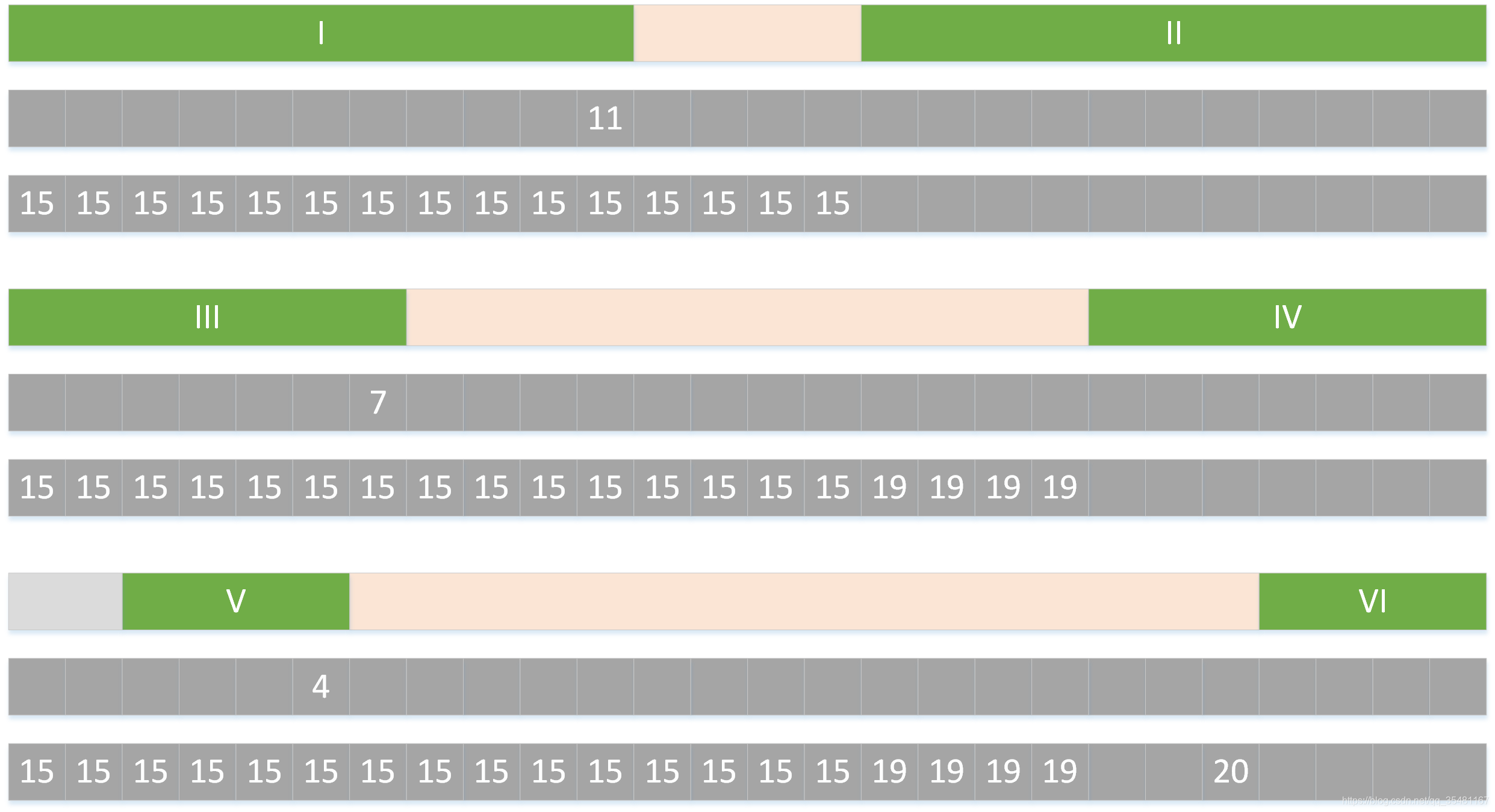
图形表示如下，第二天之后的天气概率计算后取最大值，根据第三天天气的最大概率再反推天气的路径

在这里插入图片描述

上面就是维特比算法实现的详解，下面是完整代码。

# -*- coding:utf-8 -*-
# @Time     :2019/5/27 15:30
# @author   :ding
# @filename :vertibi.py"""
维特比算法的实现
HMM 五个重要元素
S 隐藏序列的集合
K 输出状态或观测状态的集合
π对应隐藏状态的的初始概率
A 隐藏状态的转移概率 是一个N*M的概率矩阵
B 影厂状态到观测状态的混淆矩阵，是一个N*M的发射概率的矩阵
"""# 隐藏序列 S
states = ("Rainy", "Sunny")# 观测序列 K
observations = ('walk', 'shop', 'clean')# 初始概率 π
start_probability = {'Rainy': 0.6, "Sunny": 0.4}# 转移概率 A
transition_probability = {'Rainy': {"Rainy": 0.7, "Sunny": 0.3},"Sunny": {"Rainy": 0.4, "Sunny": 0.6}
}# 发射概率  B
emission_probability = {"Rainy": {"walk": 0.1, "shop": 0.4, "clean": 0.5},"Sunny": {"walk": 0.6, "shop": 0.3, "clean": 0.1},
}def print_dptable(V):print("     ")for i in range(len(V)): print("%7d" % i, end="")print()for y in V[0].keys():print("%.5s: " % y, end=" ")for t in range(len(V)):print("%.7s" % V[t][y], end=" ")print()def vierbi(obs, states, start_p, trans_p, emit_p):""":param obs:     观察序列    K:param states:  隐藏状态    S:param start_p: 初始概率    π:param trans_p: 转移概率    A:param emit_p:  发射概率    B:return:"""# 路径概率表 V[时间][隐状态] = 概率V = [{}]# 一个中间变量，代表当前状态是哪个隐状态path = {}# 初始化初始状态 t=0for y in states:V[0][y] = start_p[y] * emit_p[y][obs[0]]path[y] = [y]# 对t>0 跑一遍维特比算法for t in range(1, len(obs)):V.append({})newpath = {}for y in states:# 概率 隐状态 =  前状态是y0的概率 * y0转移到y的概率 * y表现为当前状态的概率(prob, state) = max([(V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states])# 记录最大概率V[t][y] = prob# 记录路径newpath[y] = path[state] + [y]# 不需要保存旧路径path = newpathprint_dptable(V)(prob, state) = max([(V[len(obs) - 1][y], y) for y in states])return prob, path[state]def test():return vierbi(observations,states,start_probability,transition_probability,emission_probability)print(test())

打印结果如下
输出

维特比算法在NLP方面有很多的应用

  • 词性标注：给定一个词的序列，找出最可能的词性序列
  • 分词：给定一个字的序列，找出最可能的标签序列，可利用BMES这些标签来分词B（开头）M（中间词）E（结尾）S（单个词）
  • 明明实体识别：给定一个词的序列，找出最可能的标签序列

本文讲的可能不是很清楚，有不对的地方，还请不吝指教。


http://chatgpt.dhexx.cn/article/x6v5Gl07.shtml

相关文章

维特比算法代码

维特比算法代码

维特比算法实现python语言版 本文主要写一个关于维特比算法的代码，具体理论请参考一文搞懂HMM（隐马尔可夫模型）： HMM（隐马尔可夫模型）是用来描述隐含未知参数的统计模型，举一个经典的例子&…
阅读更多...
维特比算法学习

维特比算法学习

参考文章1： 简直不要太通俗易懂，这篇文章，很值得看 参考文章2： 解释一些概念性的问题，我把他的一些内容写下来 维特比(Viterbi)算法的核心是动态规划。 对于 HMM 而言，其中一个重要的任务就是要找出最有…
阅读更多...
5分钟理解维特比算法

5分钟理解维特比算法

安德鲁维特比老人家发明了维特比算法，用非常巧妙的方法简化了隐马尔可夫第二个问题运算过程。维特比先生后来发明了CDMA技术并与人一起创办了高通公司，高通现在是通信巨头，不生产产品却每年收取大量的专利费。 下面我们用简单的例子&#xff…
阅读更多...
Viterbi-Algorithm(维特比算法)

Viterbi-Algorithm(维特比算法)

Viterbi-Algorithm 维特比算法是一个特殊但应用最广的动态规划算法。利用动态规划，可以解决任何一个图中的最短路径问题。而维特比算法是针对一个特殊的图-篱笆网了（Lattice）的有向图最短路径问题而提出来的。它之所以重要，是因为…
阅读更多...
NLP学习笔记06-维特比算法

NLP学习笔记06-维特比算法

一序 本文属于NLP学习笔记系列。 上一篇整理了前向最大匹配算法与所有组合算法缺点（时间复杂度太高了）。 二 维特比算法 log(x*y*z) log(x)log(y)log(z) 概率上为了避免小数练乘出现的超范围溢出，改用log，改用-log,使得原来求概…
阅读更多...
HMM-维特比算法

HMM-维特比算法

HMM-维特比算法（viterbi） HMM回顾隐马科夫链解法：维特比算法（Viterbi） HMM回顾 最终的公式可以解释主要分为两个部分： P(xi|yi)，发射概率，字面意思是从一个词性中发射/生成出某一个…
阅读更多...
Viterbi算法（维特比算法）

Viterbi算法（维特比算法）

维特比算法背景： 安德鲁维特比（Andrew J. Viterbi），CDMA之父，IEEE Fellow，高通公司创始人之一，高通首席科学家。他开发了卷积码编码的最大似然算法而享誉全球。1991年香农奖（Claude …
阅读更多...
HMM+维特比算法

HMM+维特比算法

一、简介 Viterbi 算法 考虑到穷举方法的缺点，可以采用：Viterbi 算法: 动态搜索最优状态序列，这样每个节点保存的是到当前节点的局部最优概率；依据最后一个时刻中概率最高的状态，逆向找其路径中的上一个最大部分最优路…
阅读更多...
维特比算法的java实现_原创：维特比算法

维特比算法的java实现_原创：维特比算法

看了宗成庆博士的《统计自然语言处理(中文信息处理)》的第六章，对维特比算法有着非常精辟的讲解。把其中的讲解上传上来，个人感觉比较正统。 今天用Java实现了这个算法，也可以转换为C代码： package com.nlp.hmm.algorithm.viterbi…
阅读更多...
隐马尔可夫(HMM)、前/后向算法、Viterbi算法 再次总结

隐马尔可夫(HMM)、前/后向算法、Viterbi算法 再次总结

本总结是是个人为防止遗忘而作，不得转载和商用。 说明：此篇是作者对“隐马尔可夫模型”的第二次总结，因此可以算作对上次总结的查漏补缺以及更进一步的理解，所以很多在第一次总结中已经整理过的内容在本篇中将不再重复&#xff0c…
阅读更多...
维特比(Viterbi)算法

维特比(Viterbi)算法

维特比算法 (Viterbi algorithm) 是机器学习中应用非常广泛的动态规划算法，在求解隐马尔科夫、条件随机场的预测以及seq2seq模型概率计算等问题中均用到了该算法。实际上，维特比算法不仅是很多自然语言处理的解码算法，也是现代数字通信中使用…
阅读更多...
小白给小白详解维特比算法（一)

小白给小白详解维特比算法（一)

小白给小白详解维特比算法（一） 小白给小白详解维特比算法一 篱笆网络Lattice的最短路径问题 这个问题长什么样子这个问题难在哪里简化成这个模样你总能回答了吧下一步我们该干什么 别倒立了我们再从头想一下这个问题 我们是怎么走过来的来我们从A开始走这…
阅读更多...
viterbi算法

viterbi算法

维特比算法（Viterbi Algorithm） 标签（空格分隔）： 未分类 维特比算法（Viterbi Algorithm） viterbi算法用于寻找最可能的隐藏状态序列(Finding most probable sequence of hidden states) 对于…
阅读更多...
维特比算法

维特比算法

1. 概述 维特比算法是安德鲁.维特比(Andrew Viterbi)于1967年为解决通信领域中的解码问题而提出的，它同样广泛用于解决自然语言处理中的解码问题，隐马尔可夫模型的解码是其中典型的代表。无论是通信中的解码问题还是自然语言处理中的解码问题&#xff0c…
阅读更多...
维特比算法（Viterbi algorithm）

维特比算法（Viterbi algorithm）

一、维特比算法(Viterbi)原理以及简单实现 维特比算法（Viterbi algorithm）是一种动态规划算法。它用于寻找最有可能产生观测事件序列的维特比路径——隐含状态序列，特别是在马尔可夫信息源上下文和隐马尔可夫模型中。 维特比算法实际是用动…
阅读更多...
机器学习：维特比算法（Viterbi Algorithm）

机器学习：维特比算法（Viterbi Algorithm）

一、维特比算法（Viterbi Algorithm）讲解方式01：篱笆网络（Lattice）的最短路径问题 已知下图的篱笆网络，每个节点之间的数字表示相邻节点之间的距离，举个例子来说，如果我走&#xff0…
阅读更多...
字符串匹配原理及实现（C++版）

字符串匹配原理及实现（C++版）

字符串匹配原理及实现（C版） 1. 字符串匹配概念2. BF2.1 原理2.2 代码实现 3. KMP3.1 原理3.2 代码实现 4. BM4.1 坏字符4.2 好后缀4.3 代码实现 1. 字符串匹配概念 在查找操作中，我们用到很重要的概念就是字符串匹配，所谓字符串匹…
阅读更多...
C++之单字符串匹配问题

C++之单字符串匹配问题

有很多算法可以解决单模式匹配问题。而根据在文本中搜索模式串方式的不同，我们可以将单模式匹配算法分为以下几种： 基于前缀搜索方法：在搜索窗口内从前向后（沿着文本的正向）逐个读入文本字符，搜索窗口中文…
阅读更多...
字符串——字符串匹配

字符串——字符串匹配

文章目录 字符串匹配一、基本概念字符串匹配问题符号和术语后缀重叠引理 二、朴素字符串匹配算法三、Rabin-Karp算法(字符串Hash算法)进制Hash质数Hash 四、利用有限自动机进行字符串匹配有限自动机字符串匹配自动机计算状态转移函数代码 五、Knuth-Morris-Pratt算法模式的前缀…
阅读更多...
朴素字符串匹配

朴素字符串匹配

描述 字符串匹配问题的形式定义： 文本(Text)是一个长度为 n 的字符串:T;模式(Pattern)是一个长度为 m 且 m≤n 的字符串:P; T 和 P 中的元素都属于有限的字母表 Σ 表; 有效位移 (Valid Shift): 如果 0≤ s ≤n-m，并且 T[s1…sm] P[1…m]&#xff0c…
阅读更多...
推荐文章

Copyright @ 2022~2023