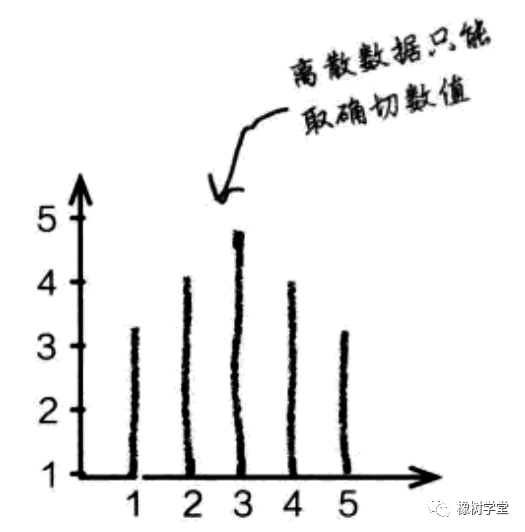
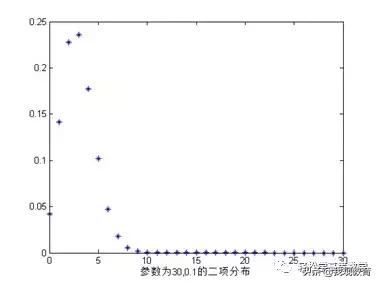
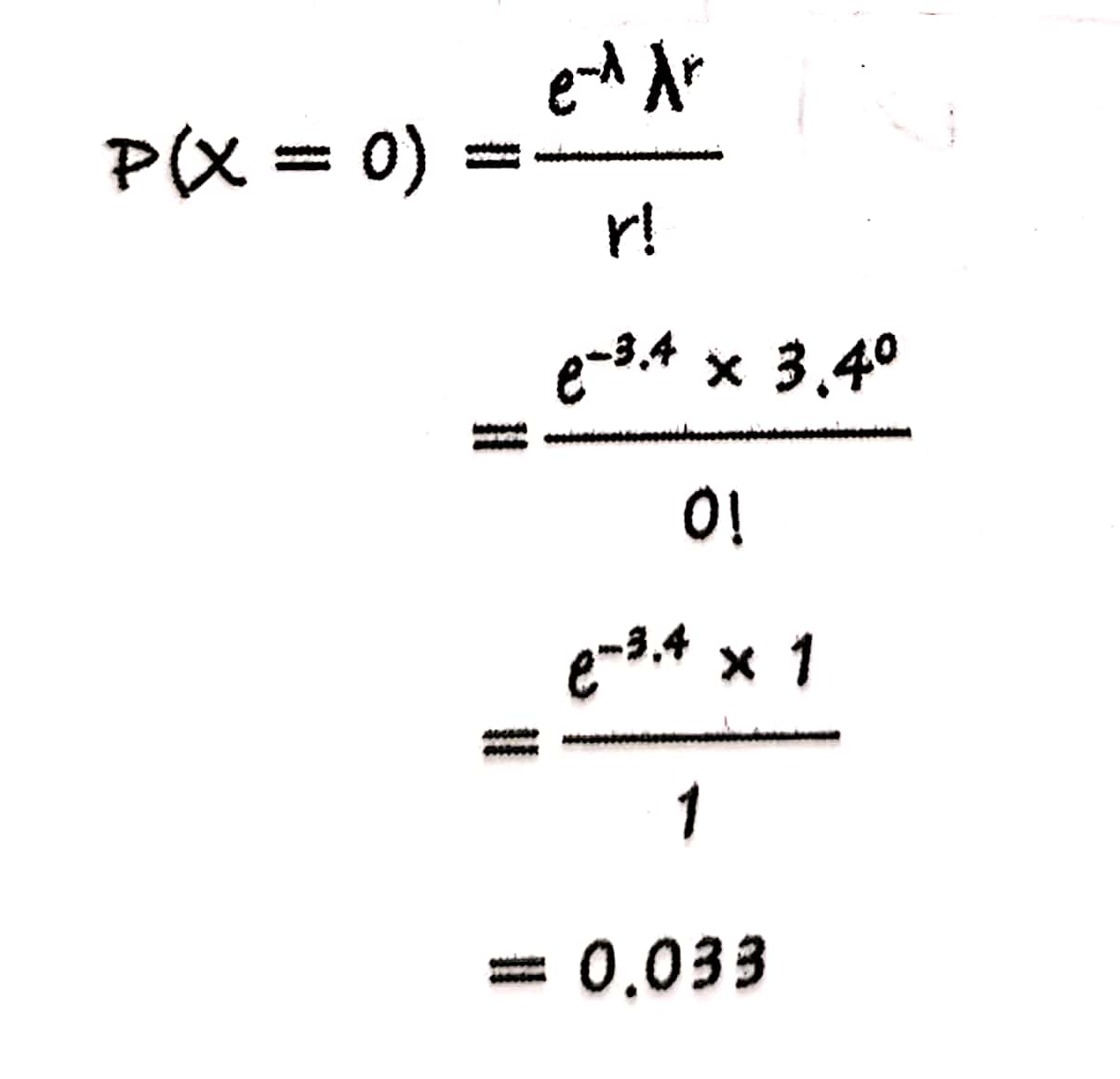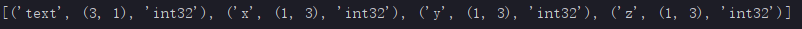与离散型随机变量相对，连续随机变量的可能结果是不可计数的。例如，如果1.250是连续随机变量的一个可能值，则不能命名下一个更高或更低的可能值。从技术上讲，连续随机变量的可能结果的范围是实线(−∞和∞之间的所有实数)或实线的某些子集。

正态分布可能是定量研究工作中应用最广泛的连续概率分布。它在现代投资组合理论和许多风险管理技术中发挥着关键作用。因为它有很多用途，所以是投资专业人士必备知识。

正态分布在统计推断和回归分析中的作用被一个称之为中心极限定理的重要结果大大扩展了。中心极限定理指出，大量独立随机变量的和(和均值)近似于正态分布。

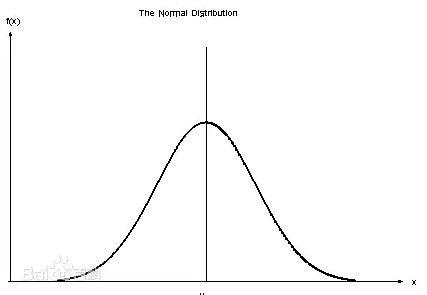
1733年，法国数学家亚伯拉罕·德莫伊夫(1667-1754)在发展中心极限定理的过程中引入了正态分布。正态分布是对称的，呈钟形，正态分布的可能结果的范围是整个实数：位于−∞和∞之间的所有实数。钟形曲线的尾巴不受限制地向左和向右延伸。

正态分布的定义特征如下：

• 正态分布完全由两个参数描述-均值μ和方差σ2.我们表示为X~N(μ，σ2)，读作“X服从正态分布，均值μ和方差σ2”。我们也可以用平均值和标准差σ来定义正态分布，这通常很方便，因为σ是用与X和μ相同的单位来测量的。因此，如果我们知道一个正态随机变量的均值和方差(或标准差)，我们就可以回答它的任何概率问题。
• 正态分布的偏度为0(它是对称的)。正态分布的峰度为3；由于对称的结果，它的超额峰度(