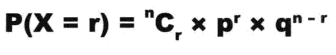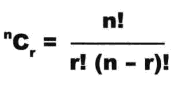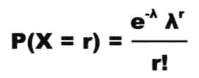离散分布主要包括3个重要的分布：几何分布、二项分布和泊松分布，这里主要介绍下这三种分布解决的典型概率问题，区别和联系。

1. 几何分布：

问题：查德在任意一次滑雪中（假定每次滑雪都是独立事件）不出事故顺利抵达坡底的概率为0.2，试问：查德不超过2次就能成功滑到坡底的概率有多大？

试滑一次成功的概率 P(X=1)=0.2

试滑两次成功的概率为P(X=2)=0.8x0.2=0.16

试滑不超过2次就成功的概率为P(X<=2)=P(X=1)+P(X=2)=0.36

查德滑雪是几何分布的一个实例，几何分布包含以下几个条件：

1）进行一系列相互独立的试验

2）每一次实验都有成功的可能，也有失败的可能，且单次成功的概率相同

3）主要感兴趣的问题是，为例取得第一次成功需要进行多少次试验。

成为几何分布，记为：X~Geo(P)

进行r次实验取得成功的概率为：

                           P(X=r)=pq^r-1

其中q=1-p为每次实验失败的概率

几何分布第一次试验取得成功的概率是最高的，其概率分布几何形状如下：

取得第一次成功需要进行r次以上试验的概率：

                           P(X>r)=q^r

取得第一次成功需要进行r次以下（包括r）试验的概率：

                           P(X>r)=1-q^r

需要进行多少次试验取得第一次成功的期望：E(X)=1/p

需要进行多少次试验取得第一次成功方差：Var(X)=q/p^2

2. 二项分布：

问题：查德在任意一次滑雪中（假定每次滑雪都是独立事件）不出事故顺利抵达坡底的概率为0.2，试问：查德试滑5次中有2次以下成功滑到坡底的概率有多大？

0次成功的概率 P(X=0)=0.8^5

1次成功的概率P(X=1)=C(5,1)x0.8^4x0.2

2次成功的概率P(X=2)=C(5,2)x0.8^3x0.2^2

试滑5次中有2次以下成功滑到坡底的概率：

P(X<=2)=P(X=0)+P(X=1)+P(X=2)

查德滑雪是二项分布的一个实例，二项分布包含以下几个条件：

1）进行一系列相互独立的试验

2）每一次实验都有成功的可能，也有失败的可能，且单次成功的概率相同

3）主要感兴趣的问题是，在有限的试验次数中，取得几次成功的概率。

条件1）和2）和几何分布一样，只是关心的问题不一样。

称为二项分布，记为：X~B(n,p)，其中n为试验次数，p为一次试验取得成功的概率

n次试验取得r次成功的概率为：          

其中q=1-p为每次实验失败的概率，

二项分布P(X=r)的分布几何形状：

取得成功试验次数的期望:

E(X)=np

取得成功试验次数的方差：

Var(X)=npq

3. 泊松分布：

问题：爆米花机器每一周的平均故障次数为3.4次，或者说爆米花机的平均故障率为3.4，试问：爆米花机器一周不初问题概率有多大？

这类问题的难点在于，尽管知道爆米花机器每一周的平均故障次数为3.4次，但实际发生故障的次数不是固定的。专门处理这种问题的分布--泊松分布。

泊松分布包括以下条件：

1）单独事件在给定区间内随机、独立发生，给定区间可以是时间或者空间，例如一星期或者一英里。

2）已经该区间时间平均发生次数（或者叫发生率），且为有限值，通常用lamda表示。

称为泊松分布，记为：X~Po(λ)

对泊松分布，给定区间内，发生r次事件的概率：

泊松分布的几何形状为：

在给定区间内，取得成功试验次数的期望:

E(X)=λ

取得成功试验次数的方差：

Var(X)=λ

回到前面的爆米花机问题，爆米花机一周内不发生故障的概率为

P(X=0)=e^-3.4 x 3.4^0/0!=e^-3.4=0.033

4）用泊松分布近似二项分布

问题：凯特是饼干厂的质量管理员，每块饼干破碎的概率是0.1，求一盒容量为100块的饼干盒子里出现15块碎饼干的概率。

是一个二项分布问题，X~(100, 0.1), 求P(X=15)=100!/(15!*85!)*0.1^15*0.9^85, 阶乘数计算太大了，普通计算器容易出现溢出问题。

 

已知X~B(n, p)，当n很大且p很小时（n>50, p<0.1），可以用X~P0(np)近似X~B(n, p)

上述问题就变为求解X~P0(10), P(X=15)的概率，带入泊松分布的概率求解方程即可求解。P(X=15)=e^-10*10^15/15!