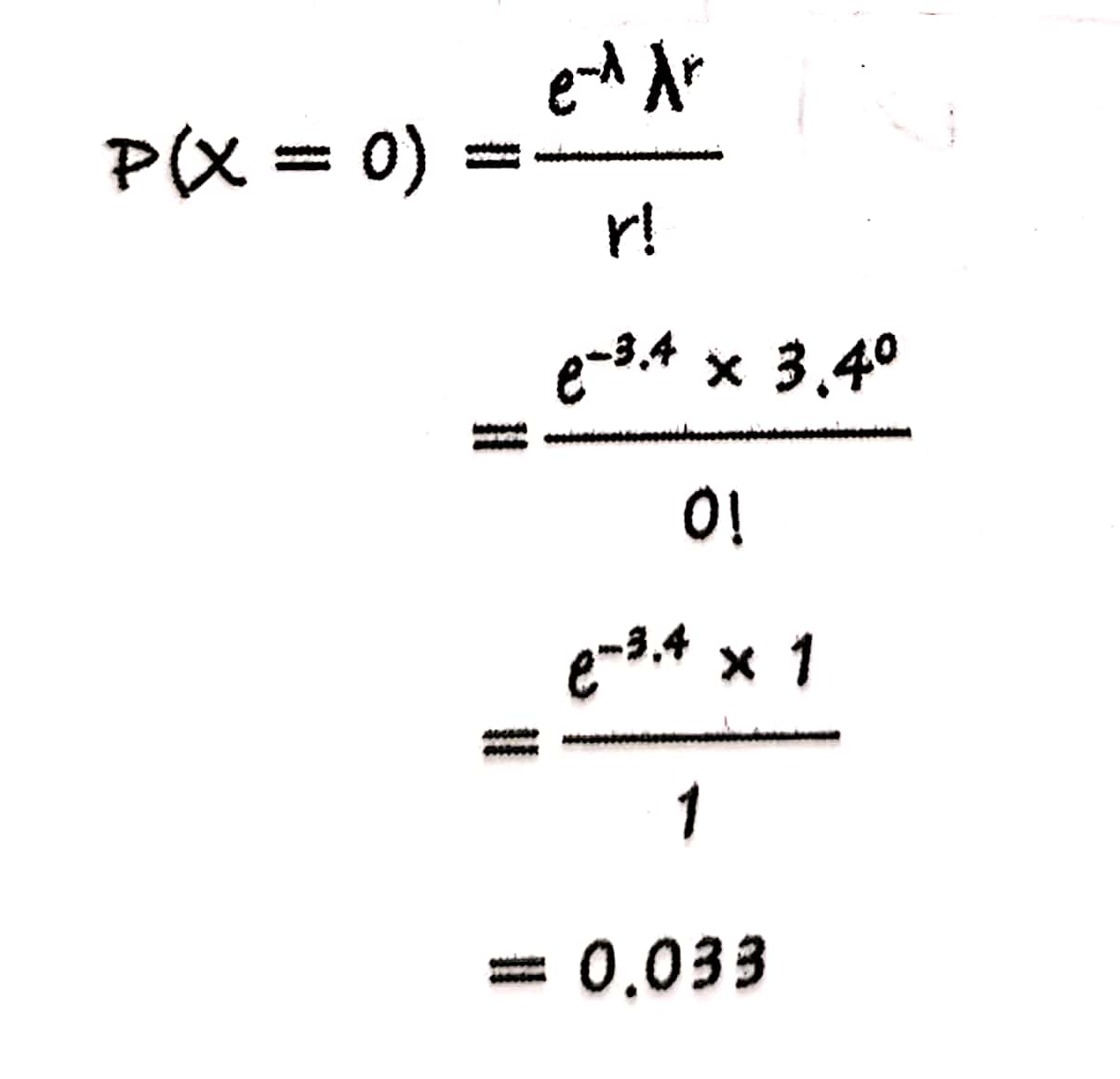这一小节我们一起学习几个离散型随机变量里的特殊的概率分布:几何分布、二项分布和泊松分布。
几何分布
乘风破浪的姐姐最近正在热播,还记得万茜小姐姐第一次个人solo的那段吉他弹唱吗?第一次她在台上弹错了,第二次虽然也有失误,但算是完整地弹了下来,假定她没有失误完成弹唱的概率是0.2,可以彩排两次,试一次或者两次就能成功的概率是多大?(如果第一次直接成功,则不进行第二次)
这是个概率的问题,还记得上一小节的内容吗?可以画个图来理解下这个问题。
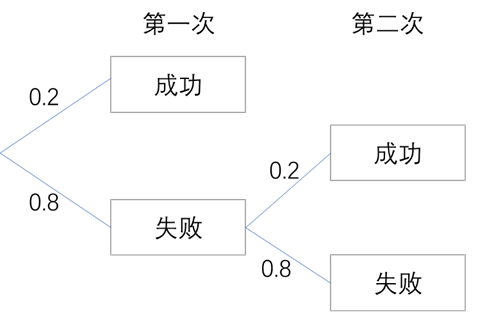
已知:
P(X=1) =P(第一次成功) = 0.2
即第一次弹唱就能成功的概率是0.2。
如何求第一次没成功第二次才成功的概率呢?就是:
P(X=2) = P(第二次成功且第一次失败) = 0.2 x 0.8 = 0.16
回到问题本身,她试弹一次或者两次就能成功的概率是多少呢?加一起:
P(X=1) + P(X=2) = 0.36
这是假设她试弹不超过3次的前提下成功的概率,那如果要求她试弹10次,100次呢?一个一个算也是可以的,但未免太麻烦了些,通过前人一次一次算的过程中总结的规律,得到了几何分布的概率可以用如下公式快速计算:
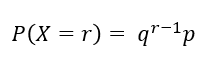
p是成功的概率,q是失败的概率(1-p),结合到我们的案例里,p就是0.2,q就是0.8,有了这个公式,就不用我们一个一个算就能得出一个一劳永逸的方法了。
回过头来我们再想一下这个案例有什么特点,也就能得出符合什么条件可以使用几何分布了:
- 进行一系列相互独立的试验
- 每次试验可能成功,也可能失败,且单次试验成功的概率相同
- 我们研究的主要是为了取得第一次成功需要进行多少次试验
代入到这个案例里就特别明显了,每次弹唱彩排都是相互独立的,每次弹唱可能成功也可能失败,且单次成功的概率都是0.2,而我们重点关心的则是首次成功需要进行多少次试验。
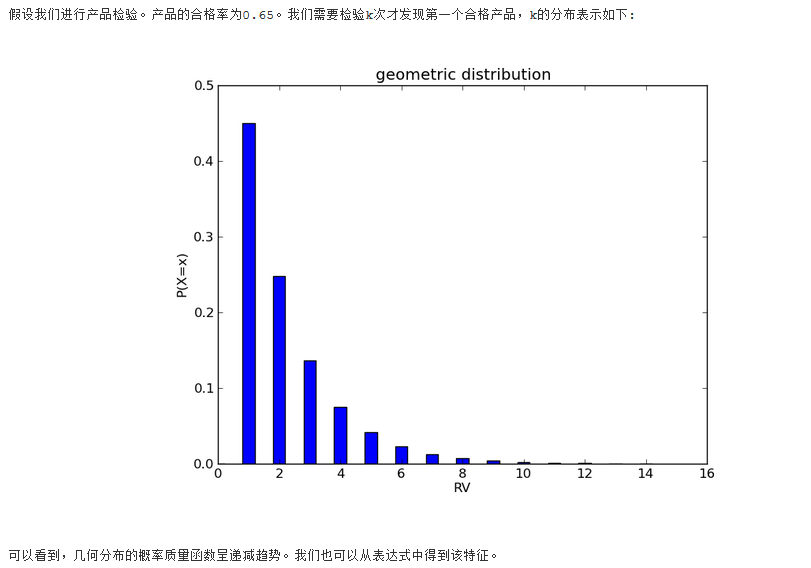
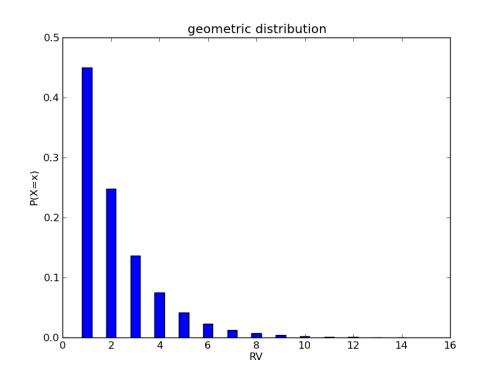
下面是几何分布的形状,可以看出来,其实仅尝试一次就成功的概率是最大的。

二项分布
假设总共有5个单选题,每个问题都有4个选项,每回答对一题的概率是0.25,回答对1到题的概率是多少呢?
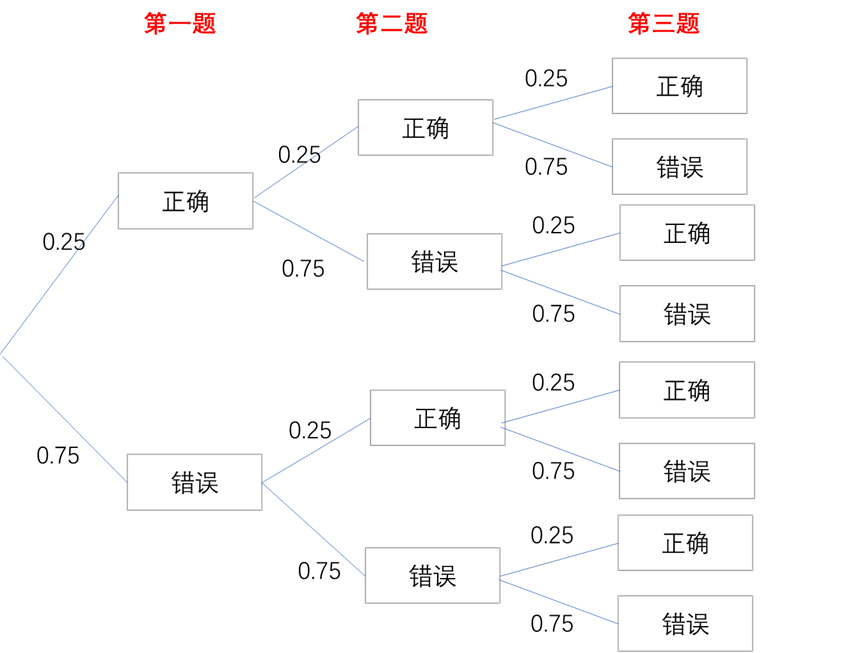
回答对一道题有3种情况:
- 第一题答对,第二题第三题答错,概率是:0.25x0.75x0.75
- 第一题答错,第二题答对,第三题答错,概率是:0.75x0.25x0.75
- 第一题答错,第二题答错,第三题答对,概率是:0.75x0.75x0.25
归纳一下,P(X=1) = 3x0.75^2x0.25
这是回答对1道题,那么回答对5道题,r道题呢?
类似上述这种单选题一样包含两个结果(答对或答错)的试验其随机变量服从的分布就是二项分布,它们的特征可总结如下:
- 一系列独立试验
- 每次试验可能成功,也可能失败,且单次试验成功的概率相同(同几何分布)
- 试验次数有限
满足二项分布模型后,X表示n次试验中的成功次数,如果要求成功r次的其概率可以用如下公式快速计算:
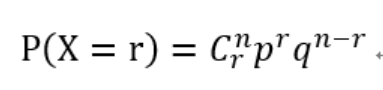
其中,
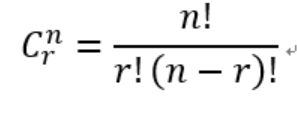
它的形状是这样的,可以看出图形比较对称。
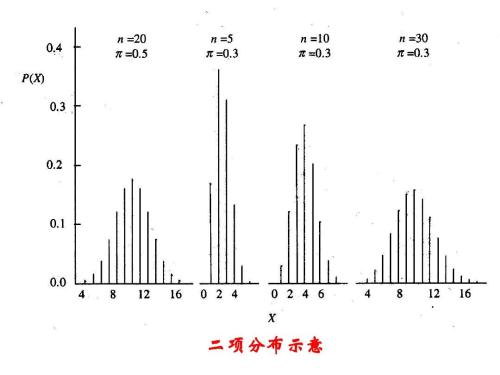

对比几何分布
相同:
- 都是独立试验
- 每次试验都有成功或失败
不同:
- 几何分布:取得首次成功前要试验多少次
- 二项分布:试验次数固定,求成功次数的概率
泊松分布
在一定时间范围内或指定面积/体积内某一事件出现的次数的分布,就属于泊松分布。
比如某企业每月发生事故的次数,单位时间内到底某一柜台的客户人数。
这与几何分布、二项分布不同,它没有一系列的试验,它是已知某一事件在特定区间内的平均发生次数,求发生r次事件的概率,符合泊松分布的条件是这样的:
- 单独事件在给定时间/空间内随机、独立地发生
- 已知该时间/空间内的事件发生率 入
满足泊松分布后,X表示给定区间内事件发生次数,发生率为 入,那么求给定区间内发生r次事件的概率就可以用如下公式计算:
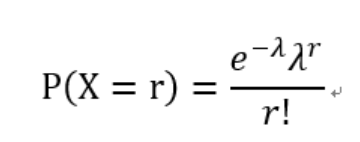
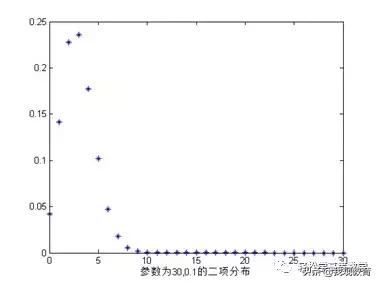
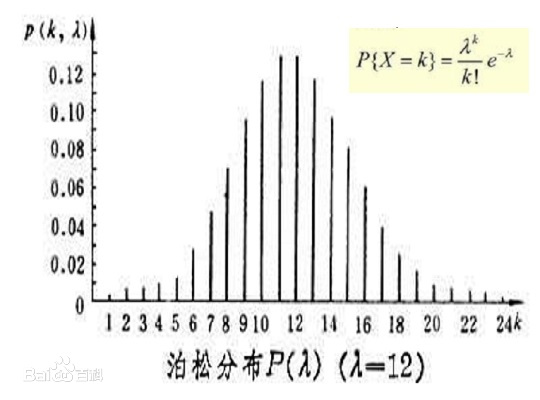
泊松分布的形状取决于入的值,入越小,分布越向右偏斜,随着入变大,分布会月对称:
比如某企业每月发生事故的次数是3.4次,要求下周不发生事故的概率,不发生事故的意思就是X=0,那么: