目录
离散分布的基础定义
经典离散分布
矩母函数 Moment Generating Function
切比雪夫定理 Tchebysheff’s Theorem
-
离散分布的基础定义
- 一个离散变量Y的概率分布可以表示成
- 每个离散概率分布都满足以下两个条件:
- 对于每个y,
,所有y的非零概率的和等于1
- 对于每个y,
- 离散变量Y的期望E(Y):
- 离散变量Y的方差V(Y):
- 一些定理关于期望E(Y)和方差V(Y)的定理:
,c是常数
- 一个离散变量Y的概率分布可以表示成
-
经典离散分布
- 二项分布 Binomial Distribution
- 几何分布 Geometric Distribution
- 超几何分布 Hypergeometric Distribution
- 泊松分布 Poisson Distribution
-
多项分布 Multinomial Distribution
-
矩母函数 Moment Generating Function
- 为什么引入矩母函数?
- 期望和标准差可以帮助确定中心和描述分布,但是它们并不是随机变量的独特特征,因为很多不同的概率分布会得出相同的期望和标准差。因此,引入矩母函数这个概念,以帮助确定某个随机变量的独特概率分布。
- 定义:
- 关于原点取的随机变量Y的第k个矩 (kth moment of a random variable Y taken about the origin) 的表达式为
或者
。
- *
- *
- 关于其期望取的随机变量Y的第k个矩 (kth moment of a random variable Y taken about its mean) 的表达式为
或者
。
- 随机变量Y的矩母函数m(t)的表达式为
。如果存在一个正常数b在
时,m(t)是有限的,则Y的m(t)存在。
- 关于原点取的随机变量Y的第k个矩 (kth moment of a random variable Y taken about the origin) 的表达式为
- 矩母函数的重要应用:
- 如果能找到m(t),则一定能找到Y的任意矩。
- 定理:如果m(t)存在,那么对于任意正整数k,
。
- 定理:如果m(t)存在,那么对于任意正整数k,
- 如果一个概率分布p(y)存在m(t),则其m(t)一定是独特的。可用该条性质建立两个概率分布的等价关系。
- 一个很好的例子:随机变量Y的m(t)为
。泊松分布在
时的m(t)也是
。由于每个概率分布的m(t)都是独特的,那么
。
- 一个很好的例子:随机变量Y的m(t)为
- 如果能找到m(t),则一定能找到Y的任意矩。
- 为什么引入矩母函数?
-
切比雪夫定理 Tchebysheff’s Theorem
- 定理:Y是一个随机变量,其期望为
, 方差为有限的
。
- 版本1:那么对于任意非零常数
,可以得到
和
。
- Y落在距离期望
的k个标准差
范围之内的概率大于等于
- Y落在距离期望
的k个标准差
范围之外的概率小于等于
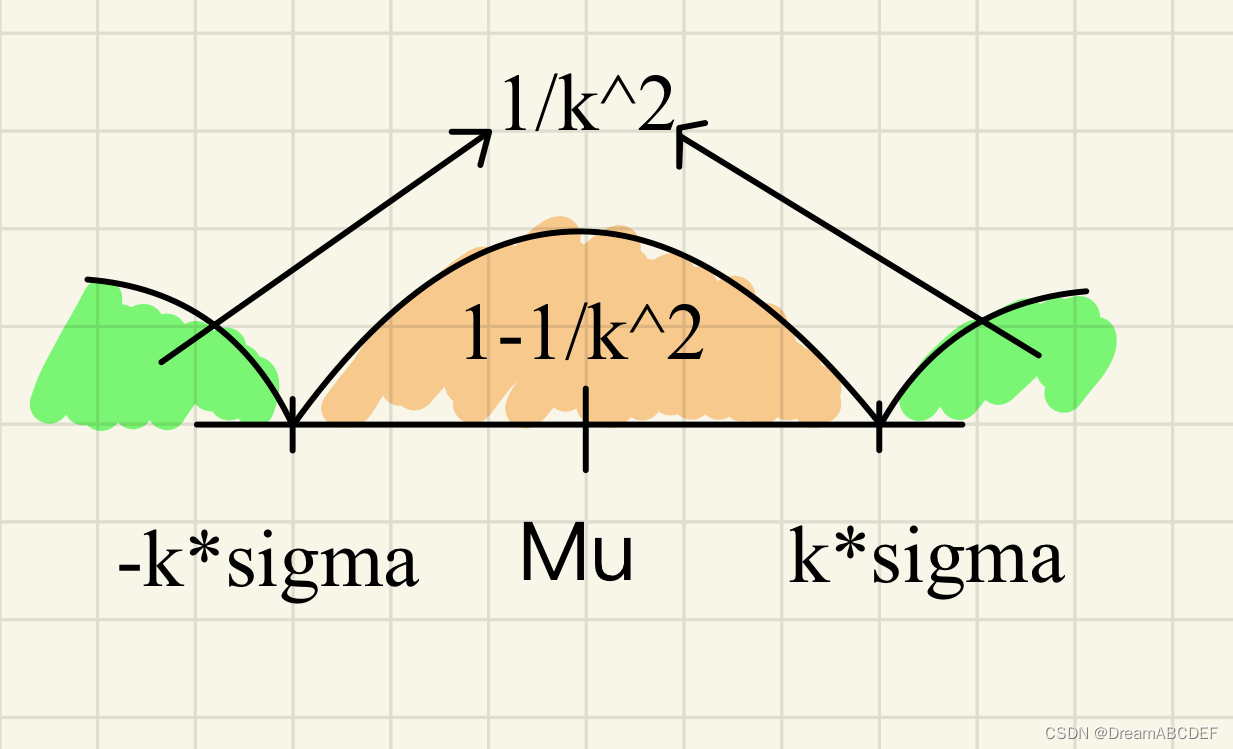
- Y落在距离期望
- 版本2:那么对于任意非零常数
,可以得到
和
- 版本1:那么对于任意非零常数
- 切比雪夫定理的两个特征:
- 对于任意概率分布都成立
- 得到的结果非常保守,真实的概率往往远超这个结果
- 定理:Y是一个随机变量,其期望为