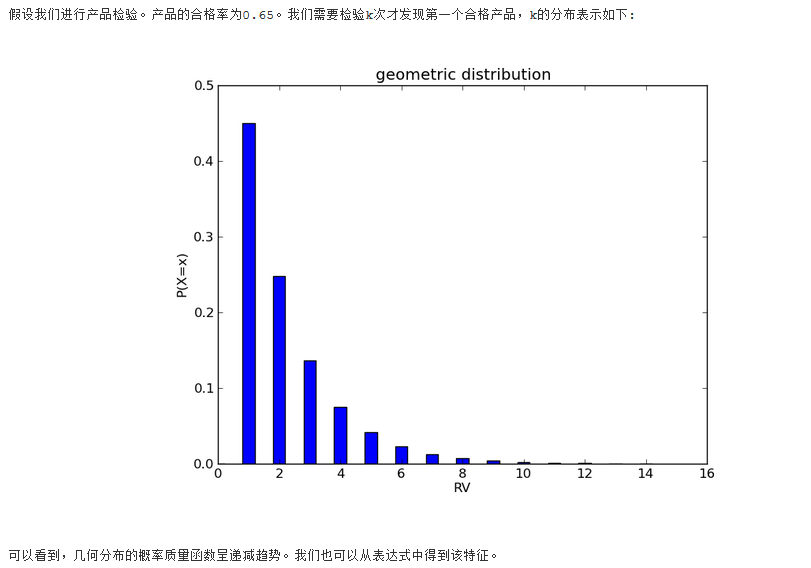
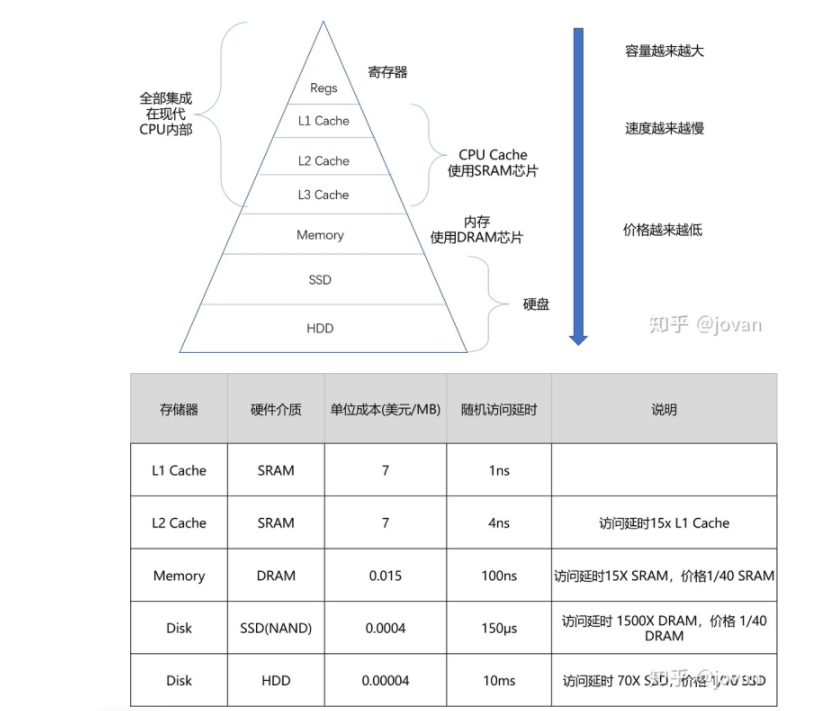
当我们对一组数据作分析的时候,一定要明确的是,这组数据只是研究对象(population)中的一部分样本(sample)。我们只是对一部分样本进行分析,然后去推测出整个对象的规律。概率分布可以很好的发现数据的内在规律;又根据随机变量所属类型的不同,概率分布取不同的表现形式
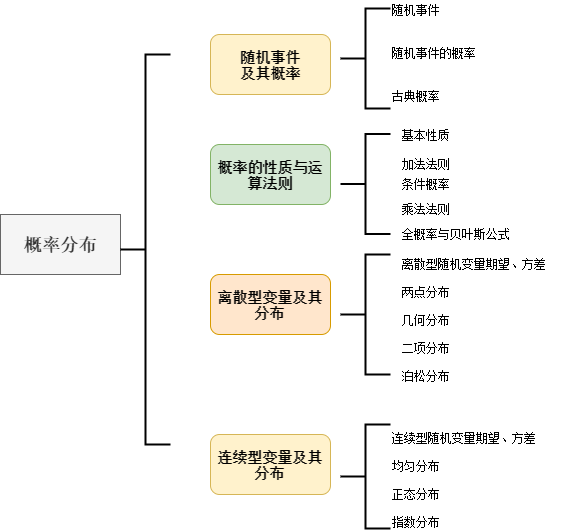
目录
随机事件及其概率
概率的性质与运算法则
离散型随机变量及其分布
连续型随机变量及其分布
一、随机事件及其概率
随机事件(random event):每次试验可能出现也可能不出现的实践。包括:简单事件,必然事件,不可能事件
随机事件的概率:事件A的概率是一个介于0和1之间的一个值,用以度量试验完成时事件A发生的可能性大小,记作P(A)
P(A) = 事件A发生的次数 / 重复试验次数 =m/n = p
古典概率
1.结果有限。如抛硬币试验中,只可能出现"正面朝上"与"反面朝上"
2.各个结果出现的可能性被认为是相同的。
P(A) = 事件A所包含的基本事件个数/样本空间所包含的基本事件个数=m/n
二、概率的性质与运算法则
概率的基本性质
1.对于任一随机事件A,有 0<=P(A) <= 1
2.必然事件概率为1,不可能事件概率为0
3.若A和B互斥,则P(A∪B) = P(A)+ P(B)
概率的加法法则
P(A∪B) =P(A) + P(B) - P(A∩B)
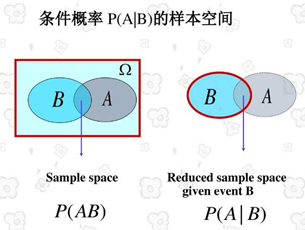
条件概率
条件概率:在事件B已经发生的条件下事件A发生的概率,称为已知事件B时事件A的概率记为
P(A|B) =P(AB)/P(B)
乘法公式(条件概率的转换)
1.用户计算两事件交的概率
2.以条件概率的定义为基础
3.设A,B为两个事件,若P(B) >0,
P(AB) =P(B)P(A|B) 或 P(AB) = P(A)P(B|A)
独立事件
1.若P(A|B) = P(A) 或 P(B|A) =P(B) ,则称事件A与B事件独立,或称独立事件
2.若两个事件相互独立,则这两个事件同时发生的概率等于它们各自发生的概率相乘
P(AB) = P(A)· P(B)
3.若事件A1,A2...An 相互独立,则P(A1,A2,...An) = P(A1) ·P(A2) ...P(An)
全概率公式与贝叶斯公式
全概率公式:
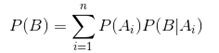
贝叶斯公式(逆概率公式):
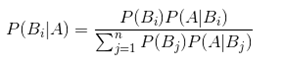
P(Bi)被称为数据Bi的先验概率(priority probability)
p(Bi|A)被称为事件Bi的后验概率( posterior probability )
三、离散型随机变量及其分布
随机变量
1.一次试验的结果数值性描述
2.一般用X,Y,Z来表示
3.根据取值情况的不同分为离线型随机变量和连续型随机变量
离散型随机变量(discrete random variable):如果表示试验结果的变量X,其可能取值至多为可列个且以各种确定的概率取这些不同的值
离散型随机变量的概率分布
1.列出离散型随机变量X的多元可能取值
2.列出随机变量取这些值的概率
3.P(X=xi) =Pi 称为离散型随机变量的概率函数
Pi>= 0 ΣPi = 1
离散型随机变量的数学期望和方差
期望
1.离散型随机变量X的所有可能取值Xi与其取对应的概率Pi乘积之和
2.描述离散型随机变量取值的集中程度
3.记为u 或者E(x)
方差
1.随机变量X的每一个取值与期望值的离差平方和的数学期望
2.描述离散型随机变量取值的分散程度
3.记作∆² 或者D(x)
4.方差的平方根为标准差
5.离散系数 = ∆ /E(x)
二项分布
二项分布是n个独立的是/非试验中成功的次数的离散概率分布,其中每次试验的成功概率为p
满足以下条件的试验成为二项试验:
1.试验由一系列相同的n个试验组成;
2.每次试验有两种可能的结果,成功或者失败;
3.每次试验成功的概率是相同的,用p来表示;
4.试验是相互独立的。
设x为n次试验中的成功的次数,由于随机变量的个数是有限的,所以x是一个离散型随机变量。x的概率分布成为二项分布。
code:
import numpy as npimport matplotlib.pyplot as plt# 二项分布list_a = np.random.binomial(n=10,p=0.3,size=1000000)# 取样1000000次,每次进行十组试验,单组试验成功概率为0.3,list_a为每组试验中成功的组数个数print(list_a)print(len(list_a))plt.hist(list_a,bins=8,color='g',alpha=0.4,edgecolor='b')plt.show()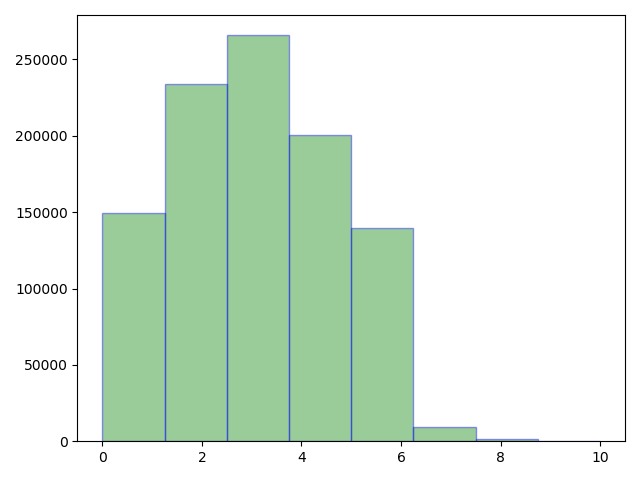
泊松分布
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。泊松分布适合于描述单位时间内随机事件发生的次数。
# 泊松分布import numpy as npimport matplotlib.pyplot as plt# 设一个某站台平均每小时会经过8辆公共汽车,求每小时经过12俩的概率list_a = np.random.poisson(8, 100000) # 试验重复100000次print(list_a)print(len(list_a))plt.hist(list_a,bins=8,color='g',alpha=0.4,edgecolor='b')plt.show()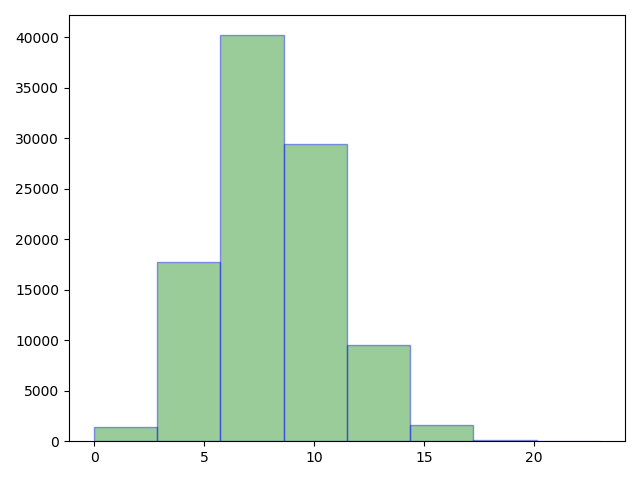
常用的离散型概率分布总结

四、连续型随机变量及其分布
连续型随机变量(continue random variable):如果表示试验结果的变量X,其可能取值为某范围内的任何数值,且X在其取值范围内的任意区间中取值时,其概率是确定的
连续型随机变量的概率分布
连续型随机变量可以取某一区间或整个实数轴上的任意一个值
它取任何一个特定的值的概率都等于0
不能列出每一个值及其相应的概率
通常研究它取某一区间值的概率
用概率密度函数的形式和分布函数的形式来描述
概率密度函数
1.设X为一连续型随机变量,x为任意实数,x的概率密度函数记为f(x) ,它满足条件
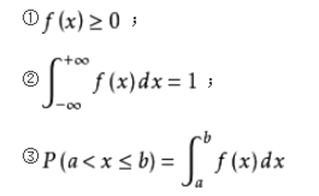
2.f(x)不是概率
连续型随机变量的期望和方差
1.连续型随机变量的数学期望
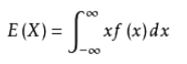
2.方差
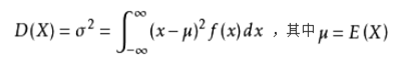
正态分布
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution)
正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形
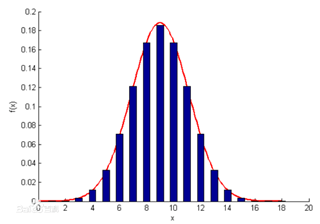
性质:
图形关于x=u对称钟形曲线,且峰值在x=u处
均值u和标准差σ一旦确定,分布的具体形式也唯一确定
均值u可取实数轴上面的任意数值,决定正态曲线的具体位置
标准差决定曲线的“陡峭”或“扁平”。σ越大,正态曲线扁平;σ越小,正态曲线月高陡峭
标准正态分布:均值为0,方差为1
code:
# 正态分布# list_d = np.random(loc,scale,size=None)#loc为期望 scale为标准差 size为取样数量,默认为None,即仅返回一个数list_d = np.random.normal(0,1,1000)plt.hist(list_d, bins=8, color='g', alpha=0.4, edgecolor='b')plt.show()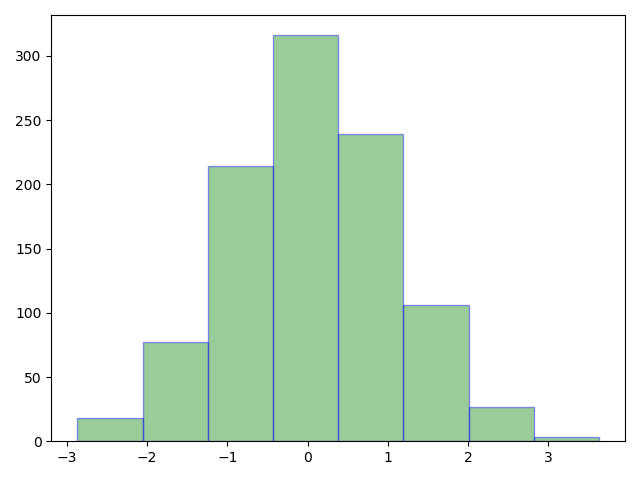
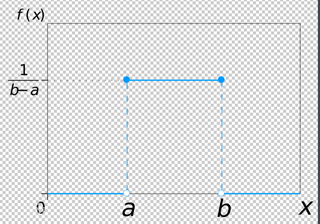
均匀分布
均匀分布的概率密度函数为:f(x) = 1/(b-a),0
数学期望和方差
E(x) = (a+b)/ 2 D(x) = (b-a)² /12
code:
import numpy as npimport matplotlib.pyplot as plt# 均匀分布list_c = np.random.uniform(0,10,10000)#low和high为分布范围 size为样本数目plt.hist(list_c,bins=8,color='g',alpha=0.4,edgecolor='b')plt.show()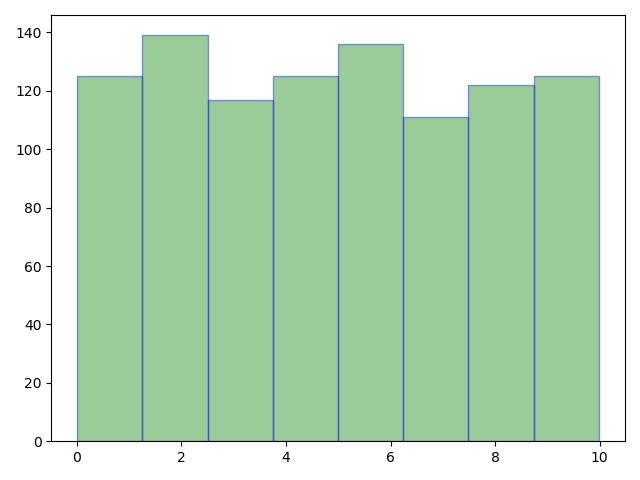
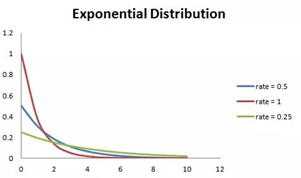
指数分布
概率密度函数:

数学期望和方差
E(x) = 1 /λ D(x) = 1 / λ²
code:
# 指数分布list_e = np.random.exponential(0.125,1000)plt.hist(list_e,bins=8,color='g',edgecolor='b',alpha=0.4)plt.show()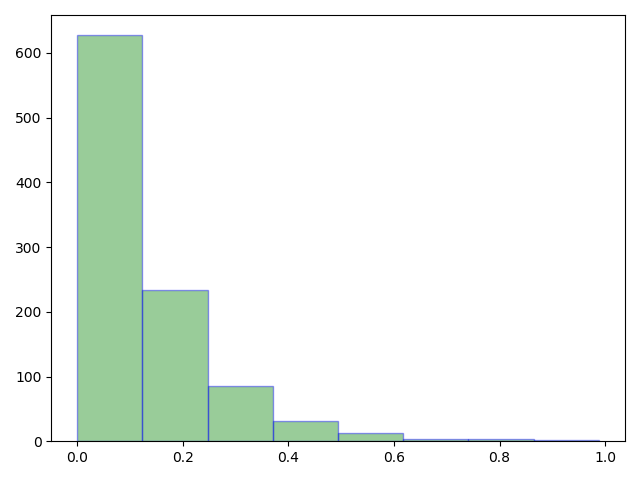
常用的连续型概率分布总结

往期精选
机器学习|梯度下降法
机器学习|逻辑回归
机器学习|决策树
机器学习|随机森林
机器学习|Adaboost
数据分析|数据的整理&展示
数据分析|数据分布特征的描述

关注公众号,加小编微信即可拉入线上交流群