vue项目打包部署流程
- 一、打包
- 二、部署
- 三、部署多个项目
一、打包
-
(可选)去除打包后会生成的map文件:在vue.config.js中添加
productionSourceMap: false,

map文件作用:项目打包后,代码都是经过压缩加密的,如果运行时报错,输出的错误信息无法准确得知是哪里的代码报错。map文件可以准确输出报错位置。
-
项目终端运行
npm run build,出现的dist文件即为打包后的文件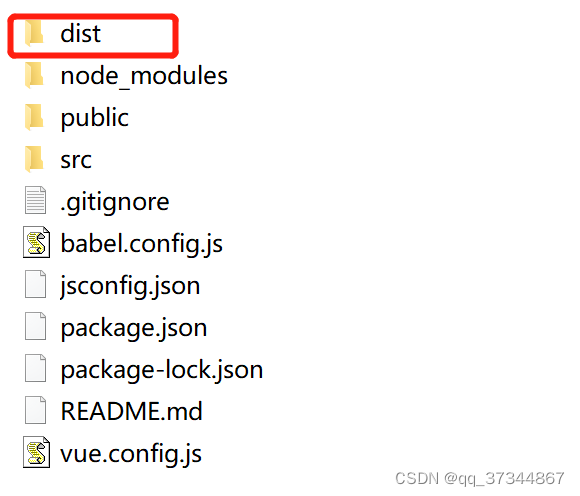
二、部署
-
xshell连接服务器(此处服务器为centos7)
-
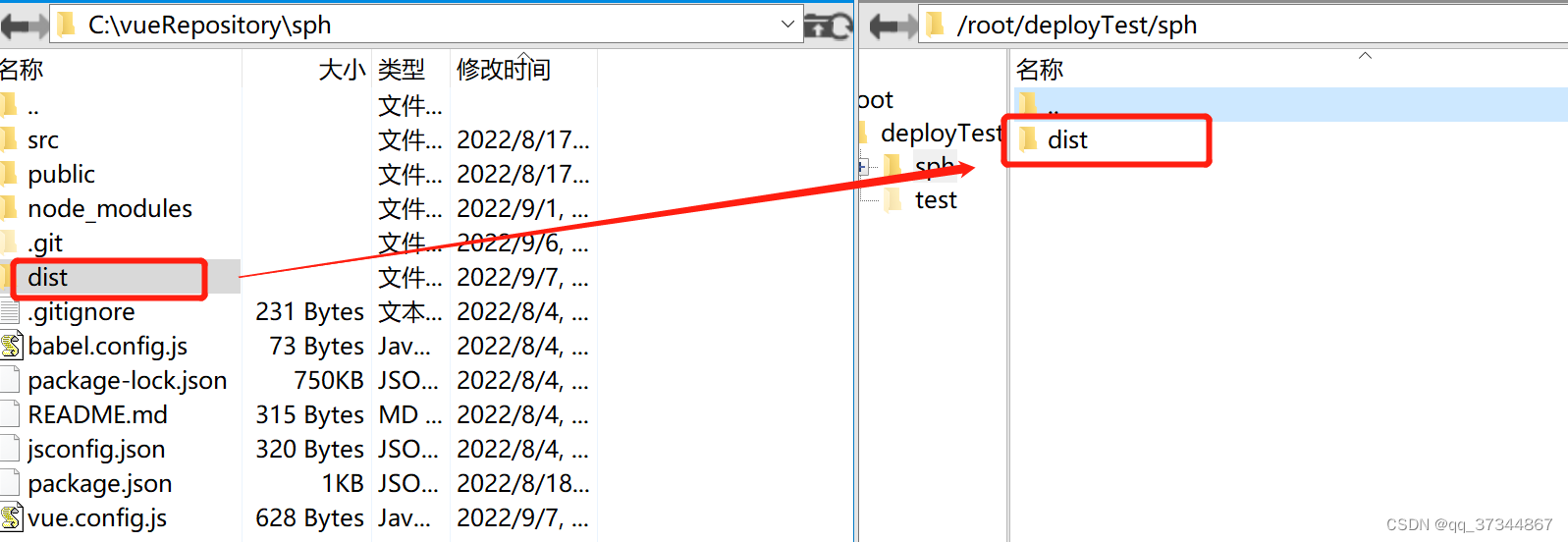
利用xfp在服务器/root目录下新建文件夹,将刚才打包生成的dist文件放到该文件夹下
-
进入/etc目录,目录中有一个nginx目录,进入该目录。如果没有nginx目录说明没有安装nginx,需要安装nginx:在/etc目录下运行
yum install nginx
-
修改nginx配置,运行
vim nginx.conf进行编辑
-
按 i 开始编辑,添加
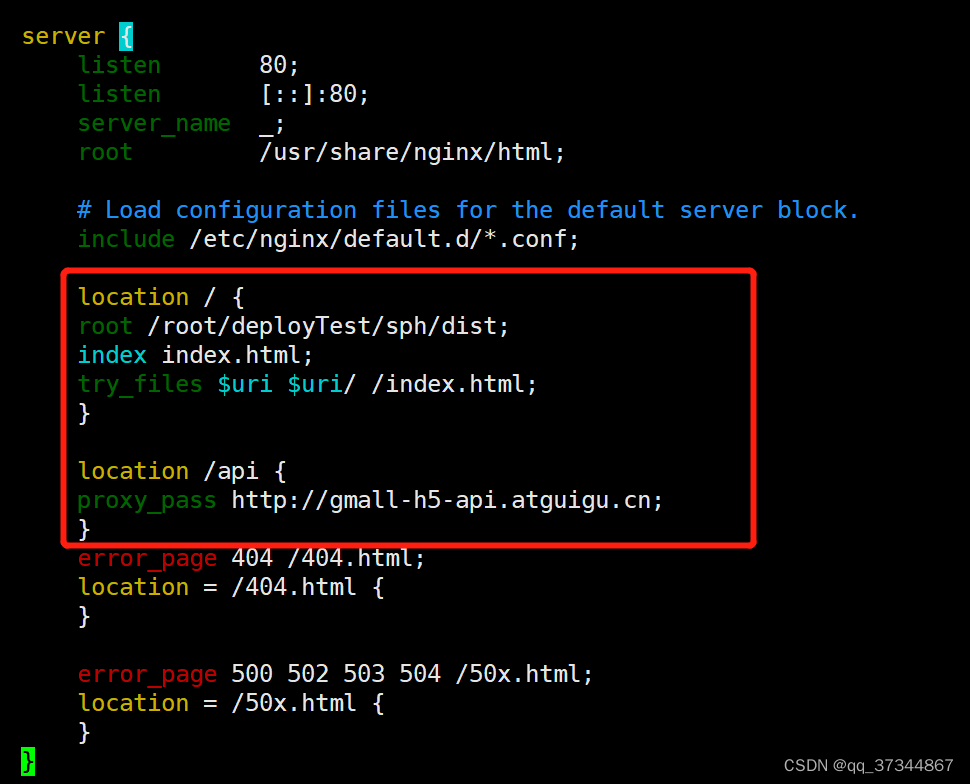
locatioin / {}配置使访问服务器即可访问到项目,为root部署到服务器的路径
location /api {}配置nginx反向代理,使得服务器可以获取从其他服务器获取的数据,/api为项目配置时代理跨域的路径名,proxy_pass为对应服务器地址注意1:添加配置时要注意空格、分号及单词拼写,由于windows和Linux空格不同,此处最好自己手写,不要复制
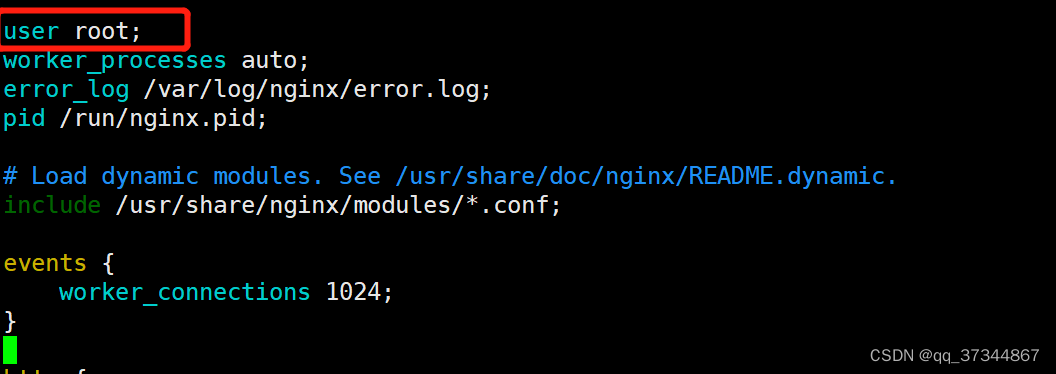
注意2:还要将开头的user nginx改成
user root,不改访问网址会报500错误注意3:修改完后restart nginx,start无效

-
按esc退出编辑
-
输入:wq进行保存
-
重新运行nginx:
systemctl restart nginx
-
访问服务器地址,即可访问到项目
注:4-8步可通过xftp直接在nginx.conf文件中进行编辑,但也要注意空格
补充:
systemctl status nginx:查看nginx状态
systemctl start nginx:启动nginx
systemctl stop nginx:停止nginx
systemctl restart nginx:重启nginx
三、部署多个项目
在nginx.conf中修改配置,访问时用服务器地址/sph即可访问