N皇后问题递归求解（内附详细代码）

内容描述

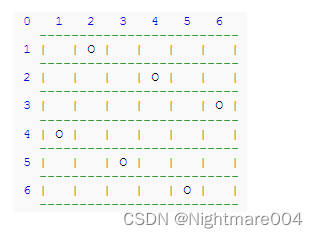
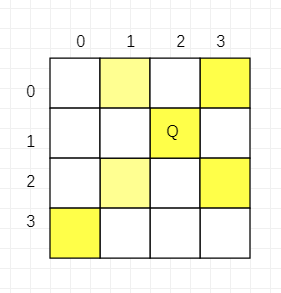
在n*n的方格棋盘上，放置n个皇后，要求每个皇后不同行、不同列、不同对角线。

解题思路

下面我们以4皇后问题举例：

设queen(i，n)是在1～i-1行上已经放好了i-1个皇后，用于在i～n行放置n-i+1个皇后“大问题”
则queen(i+1，n)表示在1～i行上已经放好了i个皇后，用于在i+1～n行放置n-i个皇后“小问题”

当(i > n) //所有皇后放置结束
else

{for(int j=1;j<=n;j++)//在第i行上试探每一个jif(place(i,j))//如果在第i行上找到一个合适的j{q[i] = j;//放置queen(i+1,n);//继续放置第i+1行}
}

详细代码如下：

#include <iostream>
#include<math.h>
using namespace std;
#define N 20 //最多皇后的个数
int q[N];//存放皇后所在列号
int count = 0;
void dispasolution(int n)//输出n皇后的一个解
{printf("   第%d个解：",++count);for(int i = 1;i<=n;i++){printf("(%d,%d)",i,q[i]);}printf("\n");}
bool place(int i,int j)//测试第（i,j）能否放置皇后
{if(i==1)return true;int k = 1;while(k<i)//k从1到i-1是已经放置皇后的行{if((q[k]==j)||(abs(q[k]-j)==abs(i-k)))//如果前面行这列已经放置或者若放在对角线上，对角线已经被放置return false;k++;}return true;
}
void queen(int i,int n)//放置1~i个皇后
{if(i > n)  //所有皇后放置结束dispasolution(n);else{for(int j=1;j<=n;j++)//在第i行上试探每一个jif(place(i,j))//如果在第i行上找到一个合适的j{q[i] = j;//放置queen(i+1,n);//继续放置第i+1行}}
}
int main()
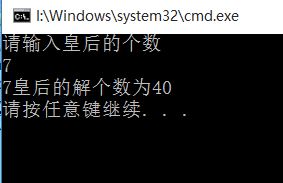
{int n;printf(" N皇后问题，n<20 n=");scanf("%d",&n);if(n>20)printf("N值太大");else{printf("N皇后解如下：\n",n);queen(1,n);}
}