回溯

#include<cstdio>
const int N = 13;
int n, cnt, ans[N];
void dfs(int row) {if (row == n) {if (cnt < 3) {for (int i = 0; i < n; ++i) {if (i > 0)printf(" ");printf("%d", ans[i] + 1);}printf("\n");}++cnt;return;}for (int i = 0; i < n; ++i) {bool flag = true;for (int j = 0; j < row; ++j) {if (ans[j] == i || row - j == i - ans[j] || j - row == i - ans[j]) {flag = false;break;}}if (flag) {ans[row] = i;dfs(row + 1);}}
}
int main() {scanf("%d", &n);dfs(0);printf("%d\n", cnt);return 0;
}

但是最后13的时候会T
在这里插入图片描述

优化1

简单来说就是哪列哪一对角线被占了先缓存一下，到时候直接查表

#include<cstdio>
const int N = 13;
bool col[N], sub_diag[2 * N - 1], main_diag[2 * N - 1];
int n, cnt, ans[N];
void dfs(int row) {if (row == n) {if (cnt < 3) {for (int i = 0; i < n; ++i) {if (i > 0)printf(" ");printf("%d", ans[i] + 1);}printf("\n");}++cnt;return;}for (int col_idx = 0; col_idx < n; ++col_idx) {int sub_diag_idx = col_idx + row, main_diag_idx = col_idx - row + n - 1;if (col[col_idx] || sub_diag[sub_diag_idx] || main_diag[main_diag_idx])continue;col[col_idx] = sub_diag[sub_diag_idx] = main_diag[main_diag_idx] = true;ans[row] = col_idx;dfs(row + 1);col[col_idx] = sub_diag[sub_diag_idx] = main_diag[main_diag_idx] = false;}
}
int main() {scanf("%d", &n);dfs(0);printf("%d\n", cnt);return 0;
}

位运算

其实就是优化1改成用位运算

#include<cstdio>
const int N = 13;
int n, cnt, ans[N], col, sub_diag, main_diag;
void dfs(int row) {if (row == n) {if (cnt < 3) {for (int i = 0; i < n; ++i) {if (i > 0)printf(" ");printf("%d", ans[i] + 1);}printf("\n");}++cnt;return;}for (int col_idx = 0; col_idx < n; ++col_idx) {int sub_diag_idx = col_idx + row, main_diag_idx = col_idx - row + n - 1;if (((col >> col_idx) | (sub_diag >> sub_diag_idx) | (main_diag >> main_diag_idx)) & 1)continue;col ^= 1 << col_idx;sub_diag ^= 1 << sub_diag_idx;main_diag ^= 1 << main_diag_idx;ans[row] = col_idx;dfs(row + 1);col ^= 1 << col_idx;sub_diag ^= 1 << sub_diag_idx;main_diag ^= 1 << main_diag_idx;}
}
int main() {scanf("%d", &n);dfs(0);printf("%d\n", cnt);return 0;
}

位运算2

每一行的副对角线：row->row+n-1
所以只要右移row位，就能找到能一列被占用了
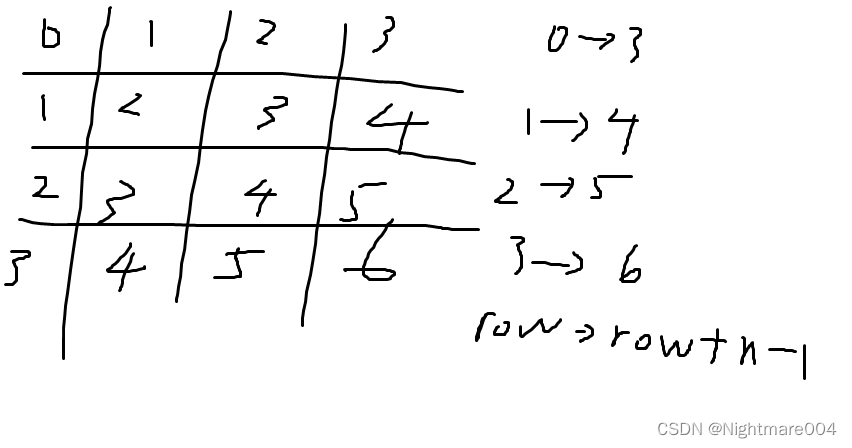
在这里插入图片描述
每一行主对角线：-row+n-1->-row+n-1+n-1
所以只要右移-row+n-1位，就能找到能一列被占用了

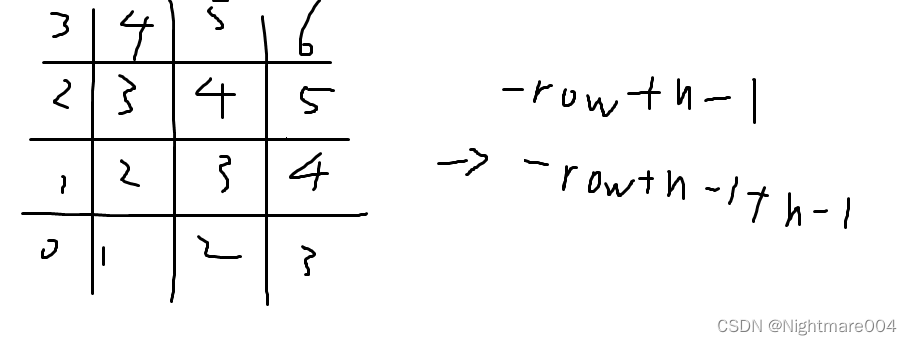
col | (sub_diag >> row) | (main_diag >> (n - 1 - row))就是被占用的列
~(col | (sub_diag >> row) | (main_diag >> (n - 1 - row)))就是可以用的列（当然还包括一些超过n的列）

#include<cstdio>
const int N = 13;
int n, cnt, ans[N], col, sub_diag, main_diag;
void dfs(int row) {if (row == n) {if (cnt < 3) {for (int i = 0; i < n; ++i) {if (i > 0)printf(" ");printf("%d", ans[i] + 1);}printf("\n");}++cnt;return;}int available = ((1 << n) - 1) & ~(col | (sub_diag >> row) | (main_diag >> (n - 1 - row)));while (available) {int p = available & (-available);available ^= p;col ^= p;sub_diag ^= p << row;main_diag ^= p << (n - 1 - row);for (int i = 0; i < n; ++i) {if ((1 << i) == p) {ans[row] = i;break;}}dfs(row + 1);col ^= p;sub_diag ^= p << row;main_diag ^= p << (n - 1 - row);}
}
int main() {scanf("%d", &n);dfs(0);printf("%d\n", cnt);return 0;
}

位运算3

col的第i位代表这一行第i列是否被占用
sub_diag的第i位代表这一行第i个副对角线是否被占用
main_diag的第i位代表这一行第i个主对角线是否被占用

dfs到下一层的时候，col不变
在第i行，假设第k个副对角线被占用了
那么在i+1行，第k-1个副对角线就被占用了
同理
在第i行，假设第k个主对角线被占用了
那么在i+1行，第k+1个主对角线就被占用了

#include<cstdio>
const int N = 13;
int n, cnt, ans[N];
void dfs(int row, int col, int sub_diag, int main_diag) {if (row == n) {if (cnt < 3) {for (int i = 0; i < n; ++i) {if (i > 0)printf(" ");printf("%d", ans[i] + 1);}printf("\n");}++cnt;return;}int available = ((1 << n) - 1) & ~(col | sub_diag | main_diag);while (available) {int p = available & (-available);available ^= p;for (int i = 0; i < n; ++i) {if ((1 << i) == p) {ans[row] = i;break;}}dfs(row + 1, col | p, (sub_diag | p) >> 1, (main_diag | p) << 1);}
}
int main() {scanf("%d", &n);dfs(0, 0, 0, 0);printf("%d\n", cnt);return 0;
}

舞蹈链

https://blog.csdn.net/qq_39942341/article/details/126681667?spm=1001.2014.3001.5501
行： $n * n$ 个格子
列： $\left[1,n\right]$ 用来记录这个数字填在了哪行
$\left[n+1,2n\right]$ 用来记录这个数字填在了哪列
$\left[2n+1,4n-1\right]$ 用来记录这个数字填在了哪条副对角线(从 $(0, 0)$ 开始)
$\left[4n,6n-2\right]$ 用来记录这个数字填在了哪条主对角线(从 $(n - 1, 0)$ 开始)

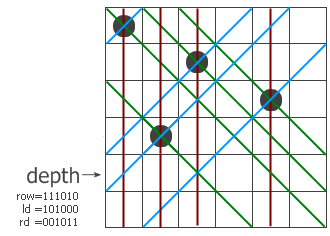
但是注意一点，对角线是无法完全覆盖的
比如下面的图，第3条副对角线就没有覆盖
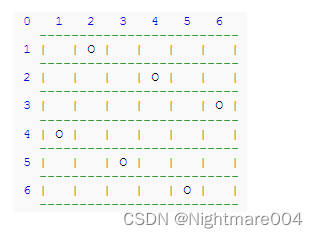
在这里插入图片描述
所以如果行和列覆盖完了就可以返回了

#include<cstdio>
#include<cstring>
#include<algorithm>const int H = 13;
const int M = H * H, N = 6 * H - 2;
int n, board_cnt;
struct A {int a[H];
}board[100000];
bool cmp(const A& a, const A& b) {int i = 0;while (i < n && a.a[i] == b.a[i])++i;return a.a[i] < b.a[i];
};
class DLX {
public:static const int MAXN = M * 4 + N + 5;int left[MAXN], right[MAXN], up[MAXN], down[MAXN];int row[MAXN], col[MAXN], head[M+5], col_size[N+5], cnt;int ans, ans_row[H];DLX() :cnt(0), ans(0) {}void init(const int& N) {cnt = ans = 0;for (int i = 0; i <= N; ++i) {left[i] = i - 1;right[i] = i + 1;up[i] = down[i] = i;}left[0] = N;right[N] = 0;memset(head, -1, sizeof(head));memset(col_size, 0, sizeof(col_size));cnt = N + 1;}void link(const int& r, const int& c) {++col_size[c];row[cnt] = r;col[cnt] = c;up[cnt] = c;down[cnt] = down[c];up[down[c]] = cnt;down[c] = cnt;if (head[r] == -1) {head[r] = left[cnt] = right[cnt] = cnt;}else {right[cnt] = head[r];left[cnt] = left[head[r]];right[left[head[r]]] = cnt;left[head[r]] = cnt;}++cnt;}void remove(const int& c) {right[left[c]] = right[c];left[right[c]] = left[c];for (int i = down[c]; i != c; i = down[i]) {for (int j = right[i]; j != i; j = right[j]) {up[down[j]] = up[j];down[up[j]] = down[j];--col_size[col[j]];}}}void resume(const int& c) {for (int i = up[c]; i != c; i = up[i]) {for (int j = right[i]; j != i; j = right[j]) {up[down[j]] = j;down[up[j]] = j;++col_size[col[j]];}}right[left[c]] = c;left[right[c]] = c;}void dance(int dep) {if (right[0]>n) {for (int i = 0; i < n; ++i) {int x = (ans_row[i] - 1) / n;int y = (ans_row[i] - 1) % n + 1;board[board_cnt].a[x] = y;}++board_cnt;return;}int c = right[0];for (int i = right[c]; i != 0 && i <= n; i = right[i]) {if (col_size[i] < col_size[c]) {c = i;}}remove(c);for (int i = down[c]; i != c; i = down[i]) {ans_row[ans++] = row[i];for (int j = right[i]; j != i; j = right[j]) {remove(col[j]);}dance(dep + 1);for (int j = left[i]; j != i; j = left[j]) {resume(col[j]);}--ans;}resume(c);return;}
};
int main() {scanf("%d", &n);DLX solver;solver.init(6 * n - 2);for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {int idx = i * n + j + 1;solver.link(idx, i + 1);solver.link(idx, n + j + 1);solver.link(idx, 2 * n + 1 + i + j);solver.link(idx, 4 * n + n + j - i - 1);}}solver.dance(0);std::sort(board, board + board_cnt, cmp);for (int i = 0; i < 3; ++i) {for (int j = 0; j < n; ++j) {if (j > 0)printf(" ");printf("%d", board[i].a[j]);}printf("\n");}printf("%d\n", board_cnt);return 0;
}