题目
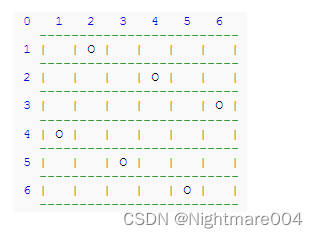
在一张N∗N的国际象棋棋盘上，放置N个皇后，使得所有皇后都无法互相直接攻击得到，（皇后可以直接攻击到她所在的横行，竖列，斜方向上的棋子），现在输入一个整数N，表示在N∗N的棋盘上放N个皇后，请输出共有多少种使得所有皇后都无法互相直接攻击得到的方案数。 例如下面这样的摆法，是4皇后的一个解 （1代表有皇后，0代表没有）
0 1 0 0
0 0 0 1
1 0 0 0
0 0 1 0

输入
一个整数N，代表皇后的个数

输出
输出方案数

样例输入
样例输入1
4
样例输入2
8

样例输出
样例输出1
2
样例输出2
92

一、DFS+回溯(1)
设已经放好的皇后坐标为(i,j),待放入的皇后坐标为(r,c)，则它们满足以下关系：
（1）不同行，即 i ≠ r；
（2）不同列，即 j ≠ c；
（3）不在斜对角线上，即 |i-r| ≠ |j-c|.
可以在一行逐列尝试，这样就不用考虑（1）了。

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
int n, tot = 0;
int col[15] = {0}, ans[15] = {0}; //col[i]的值为第i行的皇后的列数的值，即j,ans[]数组用来存放结果bool check(int c, int r) //检查是否和已经放好的皇后冲突
{for (int i = 0; i < r; i++)if (col[i] == c || (abs(col[i] - c) == abs(i - r))) //因为是逐行放置，所以只考虑纵向和斜向return false;return true;
}void dfs(int r,int m)  //在第r行放皇后,m表示行数
{if(r==m){    //r==m,即皇后放到最后一行，满足条件，tot++,返回;tot++;return;}for(int c=0;c<m;c++) //在此行逐列尝试if(check(c,r)){   //检查是否冲突col[r]=c;       //不冲突就在此列放皇后dfs(r+1,m);     //转到下一行继续尝试}
}int main()
{cin>>n;for (int i = 0; i <= 13; i++) //算出所有N皇后的答案，先打表，不然会超时{memset(col, 0, sizeof(col)); //清空col，准备计算下一个N皇后问题tot = 0;dfs(0,i);ans[i] = tot;}cout << ans[n] << endl;return 0;
}

在上述程序中，dfs()一行行放置皇后，时间复杂度为O(N!)；check()判断冲突，时间复杂度为O(N)，总的为O(N*N!)！非常的高。

二、DFS+回溯（2）

#include <iostream>
#include <algorithm>
using namespace std;int tot = 0, n;
int col[20] = {0}; //col[]含义和上面一样，表示列的值jvoid dfs(int r)
{if (r == n)tot++; //达到递归边界，方案数加一elsefor (int i = 0; i < n; i++){int flag = 1;col[r] = i;                 //尝试把第r行皇后放在第i列for (int j = 0; j < r; j++) //检查是否和前面的皇后冲突if (col[r] == col[j] || r - col[r] == j - col[j] || r + col[r] == j + col[j]){flag = 0;break;}if (flag)dfs(r + 1);}
}int main()
{cin >> n;dfs(0);cout << tot << endl;return 0;
}

优化：
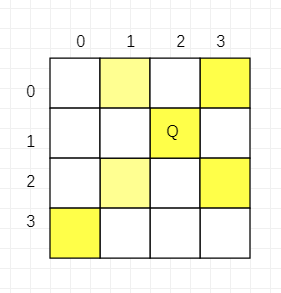
既然皇后是逐行放置的，因此只需要检查纵向和斜向是否攻击即可。纵向好判断，对于斜向，我们可以把格子的坐标设置成(x,y)，用(y-x)标识主对角线的值，用(y+x)表示副对角线的值（当然也可以反过来）。这是会发现对于主或副每一条对角线的值是一样且唯一的（其实也不太严谨）。如下图所示：

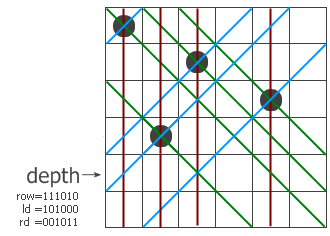
在此，我们设置一个二维数组vis[3][2n](为什么是2n接下来会讲到），用vis[0][i]表示i列是否放置皇后，vis[1][r+i]（即y+x）表示副对角线是否皇后，用vis[2][r-i+n]（即y-x,+n是防止出现负数）表示主对角线是否放置皇后。接下来就简单了，和上面想法一样，对于每一行，从0开始逐列尝试放置皇后，如果在这行的i列中，vis[0][i]和vis[1][r+i]和vis[2][r-i+n]都为零，即这个格子(r,i)的纵向和两个斜向都没有皇后，就在此处放置皇后，并标记这个格子的纵向和两个斜向都已经不能放置皇后（因为这个位置放了新皇后）也就是令vis[0][i] = vis[1][r+i] = vis[2][r-i+n] = 1;继续尝试下一行，最后别忘了取消标记（vis[0][i] = vis[1][r+i] = vis[2][r-i+n] = 0）。

主要思路就是这样，有一些需要注意的细节。因为r-i+n的值最大会达到2n-1,所以最少要设置vis[3][2n]，当然大一点会更好。还有就是细心的同学会发现在上面的主对角线中，y-x+n后会有不同的对角线有相同值，其实不用太在意，因为判断条件是同时判断三个（纵向和两个斜向），而对于每一个格子，其三向坐标是唯一的（y，y-x(+n)，y+x)。

下面是代码：

#include <iostream>
#include <algorithm>
using namespace std;
int vis[3][45]={0},c[20]={0},tot=0,n; //c[i]表示在i行皇后放置的列的值j，主要为了打印结果;vis[3][]是用来判断的数组，tot存放答案void dfs(int r)
{if(r==n) tot++;  //递归边界，走到最后一行说明方案可行，tot++else for(int i=0;i<n;i++){   //在r行逐列尝试放皇后if(!vis[0][i] && !vis[1][r+i] && !vis[2][r-i+n]){ //如果(r,i)格子的三个方向都没有皇后c[r] = i; //在i列放置皇后，如果不用打印解，可以省略整个c[]vis[0][i] = vis[1][r+i] = vis[2][r-i+n] = 1; //标记dfs(r+1);  //向下一行尝试vis[0][i] = vis[1][r+i] = vis[2][r-i+n] = 0; //取消标记}}
}int main()
{cin>>n;dfs(0);cout<<tot<<endl;return 0;
}

三、
PS：看到还有大佬是用动态规划、公式甚至是位运算做的，以后有空再研究吧，先挖坑。

四、N皇后的一些解
n solution(n)
1 1
2 0
3 0
4 2
5 10
6 4
7 40
8 92
9 352
10 724
11 2680
12 14200
13 73712
14 365596
15 2279184
16 14772512
17 95815104
18 666090624
19 4968057848
20 39029188884
21 314666222712
22 2691008701644
23 24233937684440
24 227514171973736
25 2207893435808352