n皇后 - 位运算版

article/2025/10/14 3:44:51

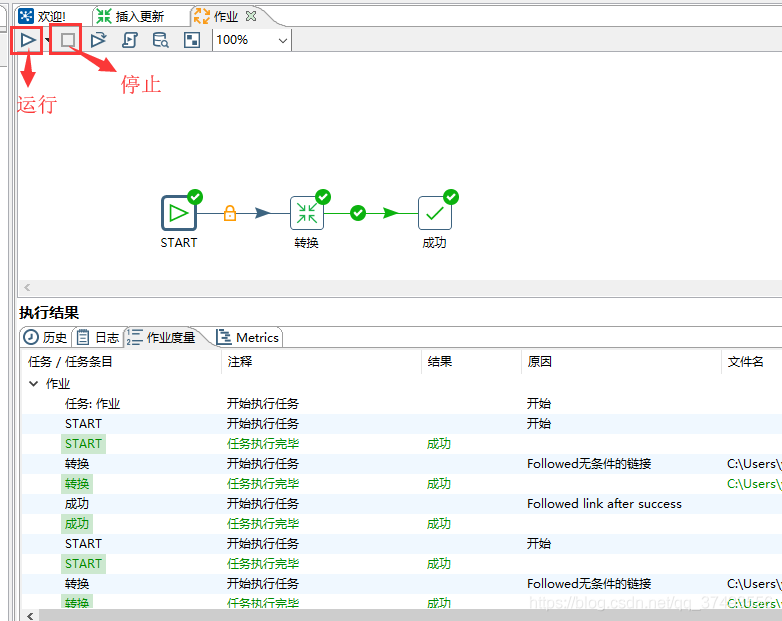
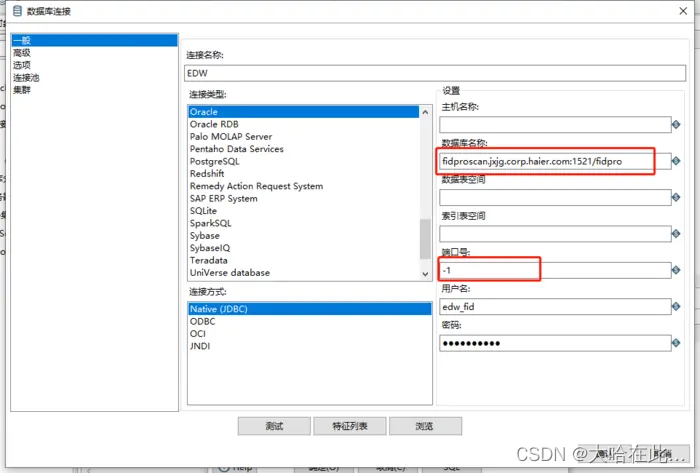
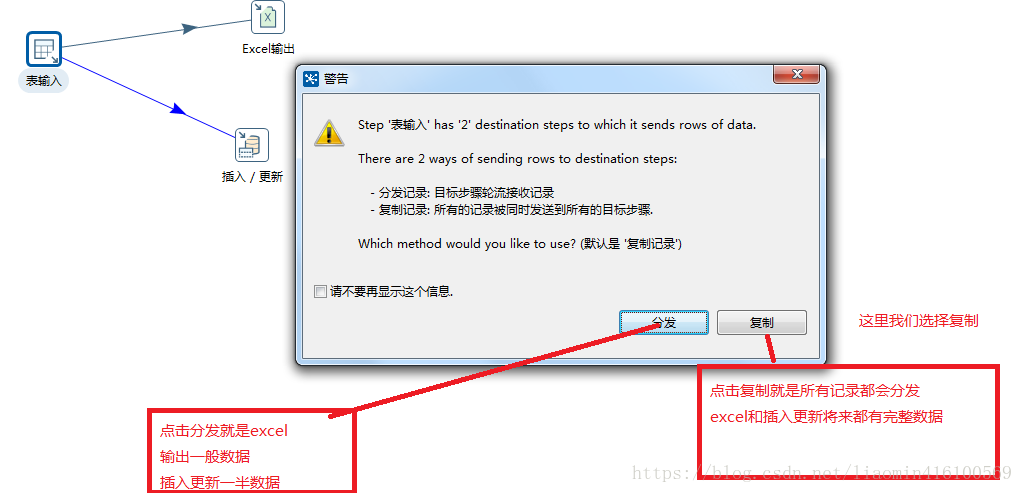
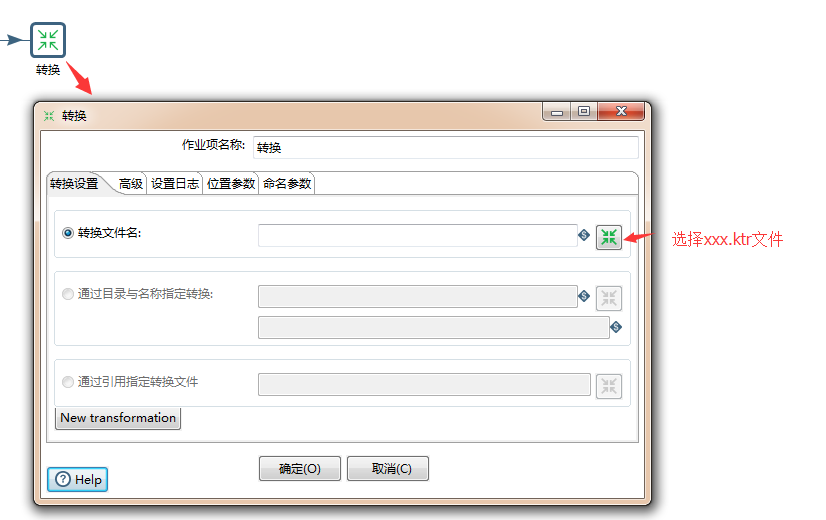
n皇后问题是大家在递归里会碰到的一个经典问题。以前高中我学DFS的时候，老师首先让我看的就是八皇后。

不过这皇后的时间复杂度大家可想而知了。而接下来的位运算将这个效率重新提到一个高度。

我是以前在Matrix67大牛那里学的，最近数据结构实验刚好碰到n皇后，就在这里“复述”一遍吧。

Code: 
void doans(int r, int ld, int rd)  
{  
    if(r != uplimit)  
    {  
        int pos = uplimit & ~(r | ld | rd);  
  
        while(pos != 0)  
        {  
            int p = pos & (~pos + 1);  
            pos -= p;  
            doans(r + p, (ld + p) << 1, (rd + p) >> 1);  
        }  
    }  
    else sum++;  
}  

乍一看有点模糊吧？没错，这就是n皇后的递归函数了。我们一个个来解析。

首先uplimit是(1 << n) - 1，如果n是8的话uplimit就是255，看做二进制就是11111111。聪明的人一看就知道了，这里每一位就代表一个皇后。

而r代表每一列能放与否，如10001110就代表第2、3、4、8个能放。

所以开始一个if来判断皇后放齐了没。如果齐了，显然r也要等于11111111。

还有ld和rd分别是对角线的各位能放与否。

我们来看看下图(From Matrix67)：

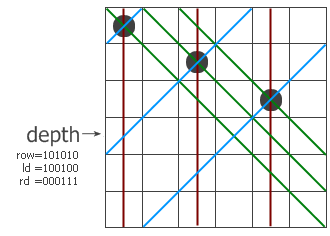
假设我们已经递归到第三行了（左图），这里可以看出r为101010也就是说二、四、六可以放。ld是100100（蓝色线），二、三、五、六可以放，rd为000111,。

好的，那么哪几个可以放呢？我们将r、ld、rd或运算一遍（或者r有或者ld有或者rd有），得到101111，也就是说这三个合起来的话就只能放第二格了。然后我非运算一遍，得到的是010000，非运算之后1代表可以放，0代表不可以放了。然后我们再与运算一遍就得到可以放的位置了：010000。

下一步，如果能放的位置不是0的话我们就开始放：

Code: 
int p = pos & (~pos + 1);  

这一句我们可以用

Code: 
int p = pos & -pos;  

来代替，什么意思呢？其结果是取出最右边的那个1。比如我们有一个数字pos是10010，那么p得到的结果就是10了。那么上面那个010000得到的结果就是10000了。然后我们更新一遍pos：让它减去p也就是10000，那么pos得到的结果就是000000。也就是说下一次循环就跳出了。

好的，我们不管下一次循环，我们讲怎么进入下一层递归：

看看传进去的三个参数：

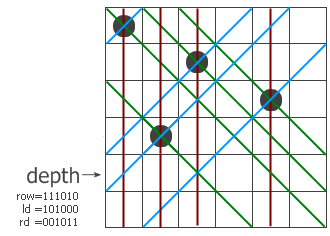
r + p为下一层递归的r，即10000 + 101010 = 111010那就相当于放进第二个了。

(ld + p) << 1为下一层的ld，即(100100 + 10000) << 1为(110100) << 1也就是1101000了。当然，在下一层递归的时候第一个1将会被uplimit & ~(r | ld | rd)截掉成为101000。

(rd + p) >> 1为下一层的rd，即(000111 + 10000) >> 1为(010111) >> 1也就是001011。

那么在新的一层里又有新的r和ld还有rd组合了。

主题的思路就是这样子的。

最后方便大家理解学习，发下我的n皇后代码：

Code: 
/** 
 * @brief n皇后问题 - 位运算版 
 * @Author 朱凯迪 
 * 2010/11/22 
 */  
#include <iostream>  
#include <list>  
using namespace std;  
  
/** 方案链表 */  
list<int> sol;  
  
/** 棋盘大小 */  
int n;  
/** 棋盘摆满时的数字 */  
int uplimit;  
  
void print()  
{  
    printf("/n");  
    list<int>::iterator i;  
    for(i = sol.begin(); i != sol.end(); i++)  
    {  
        int tmp = *i, cnt = 0;  
        while(tmp != 1)  
        {  
            cnt++;  
            tmp = tmp >> 1;  
        }  
        for(int j = 0; j < cnt; j++) printf("■");  
        printf("○");  
        for(int j = cnt + 1; j < n; j++) printf("■");  
        printf("/n");  
    }  
    printf("/n");  
}  
  
void doans(int r, int ld, int rd)  
{  
    if(r != uplimit)  
    {  
        /** 还没摆满 */  
  
        /** 取能放的位置 */  
        int pos = uplimit & ~(r | ld | rd);  
  
        /** 若还有位置如00001011表示能放5、7、8位 */  
        while(pos != 0)  
        {  
            /** 取低位 */  
            int p = pos & (~pos + 1);  
  
            /** 更新位置 */  
            pos -= p;  
  
            /** 答案入 */  
            sol.push_back(p);  
  
            /** 更新禁手并进行下一层更新 */  
            doans(r + p, (ld + p) << 1, (rd + p) >> 1);  
  
            /** 答案出 */  
            sol.pop_back();  
        }  
    }  
    else print();  
}  
  
int main()  
{  
    while(cin >> n)  
    {  
        /** 如n为8，则uplimit为11111111 */  
        uplimit = (1 << n) - 1;  
        doans(0, 0, 0);  
    }  
  
    return 0;  
}  