题目
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。等价于要求任何两个皇后都不能在同一行、同一列以及同一条斜线上
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
如图:黄色代表放置皇后的位置

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位
例如:
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。解题的思路:
1,首先我们以行为基准,我们放置了第一行,那么只能去第二行寻找可以放置皇后的位置,以此类推,指导最后一行,如果到最后一行都能将皇后放置进去,说明这是一个可行的方案,
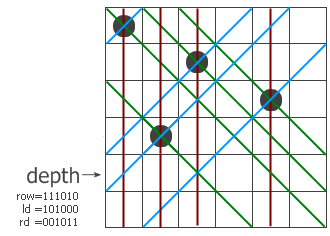
2,首先一个皇后放在了第一行,那么,它所在的列,以及交叉线都不能放置皇后了,那么我们怎么用状态标识呢,那我们不妨每列,和两个交叉线都用一个集合存放,每列我们好表示,把第一列或者第二列放到集合里说明,这列被用了,那么两个交叉线怎么表示呢?
如图,当皇后放置在(1,2)这个位置:
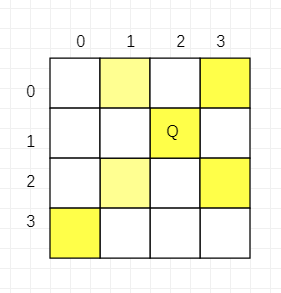
左上向下的这条斜线:
它们的位置分别是(0,1),(1,2),(2,3)那么每个坐标里的行坐标减去列坐标,0-1 == 1-2 == 2-3 ==-1,正好是等值。
右上向下的这条斜线:
它们的位置分别是(0,3),(1,2),(2,1),(3,0),那么每个坐标里的值相加,0+3 == 1+2== 2+1 == 3+0 ==3 ,正好是等值。
哈哈,是不是很神奇,你们自己随便找个位置试一下,是不是都有一个等值,并且都不重复,那么我们就把相应的值加入到集合里面,是不是就能标识,是不是这些位置都不能放置皇后了
3,接着我们就是用回溯去找每一种可能
知道上面的几点,代码就好理解了呢,现在我们去看一下,代码,有很多可以改良的地方,请大家多多指教
public static List<List<String>> solveNQueens(int n) {//存放最终答案的集合List<List<String>> list = new ArrayList<List<String>>();//标识那些列不能被用了,不能放置皇后了List<Integer> cloums = new ArrayList<Integer>();//标识右上向下的斜线,不能放置皇后了List<Integer> rDiagonals = new ArrayList<Integer>();//标识左上向下的斜线,不能放置皇后了List<Integer> lDiagonals = new ArrayList<Integer>();List<int[]> result = new ArrayList<>();//用于标识每一组(行),-1标识没有放置皇后,1标识为皇后int[] queens = new int[n];Arrays.fill(queens, -1);return dolt(n, queens, result, list, cloums, rDiagonals, lDiagonals, 0);}public static List<List<String>> dolt(int n, int[] queens, List<int[]> result, List<List<String>> list, List<Integer> cloums, List<Integer> rDiagonals, List<Integer> lDiagonals, int row) {if (row == n) {list.add(transFromToString(result));return list;}for (int col = 0; col < n; col++) {if (cloums.contains(col)) {continue;}if (rDiagonals.contains(row + col)) {continue;}if (lDiagonals.contains(row - col)) {continue;}//值为1时表明该位置是皇后queens[col] = 1;//为了将该组存入集合,需要新new一个数组,利用深拷贝,把queens数组里面的值拷贝过来,当queens重置时不会影响到该数组int[] replaceQueen = new int[n];replaceQueen = queens.clone();result.add(replaceQueen);//将列,两个交叉线,标识为不能在放置皇后了cloums.add(col);rDiagonals.add(row + col);lDiagonals.add(row - col);//重置queensArrays.fill(queens, -1);dolt(n, queens, result, list, cloums, rDiagonals, lDiagonals, row + 1);//重置状态//list.remove(),有两个方法,一个是list.remove(Object object)删除的是元素,一个是list.remove(Integer integer)删除的是该索引result.remove(result.size() - 1);cloums.remove(new Integer(col));rDiagonals.remove(new Integer(row + col));lDiagonals.remove(new Integer(row - col));}return list;}public static List<String> transFromToString(List<int[]> queens) {List list = new ArrayList();for (int[] a : queens) {char[] ch = new char[a.length];Arrays.fill(ch, '.');for (int i = 0; i < a.length; i++) {if (a[i] != -1) {ch[i] = 'Q';}}list.add(new String(ch));}return list;}