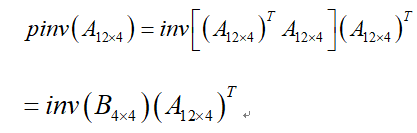1. LU分解

LU分解(LU Factorization)可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积。LU分解非常简单，下图可以直观的看出LU分解的求解方法。

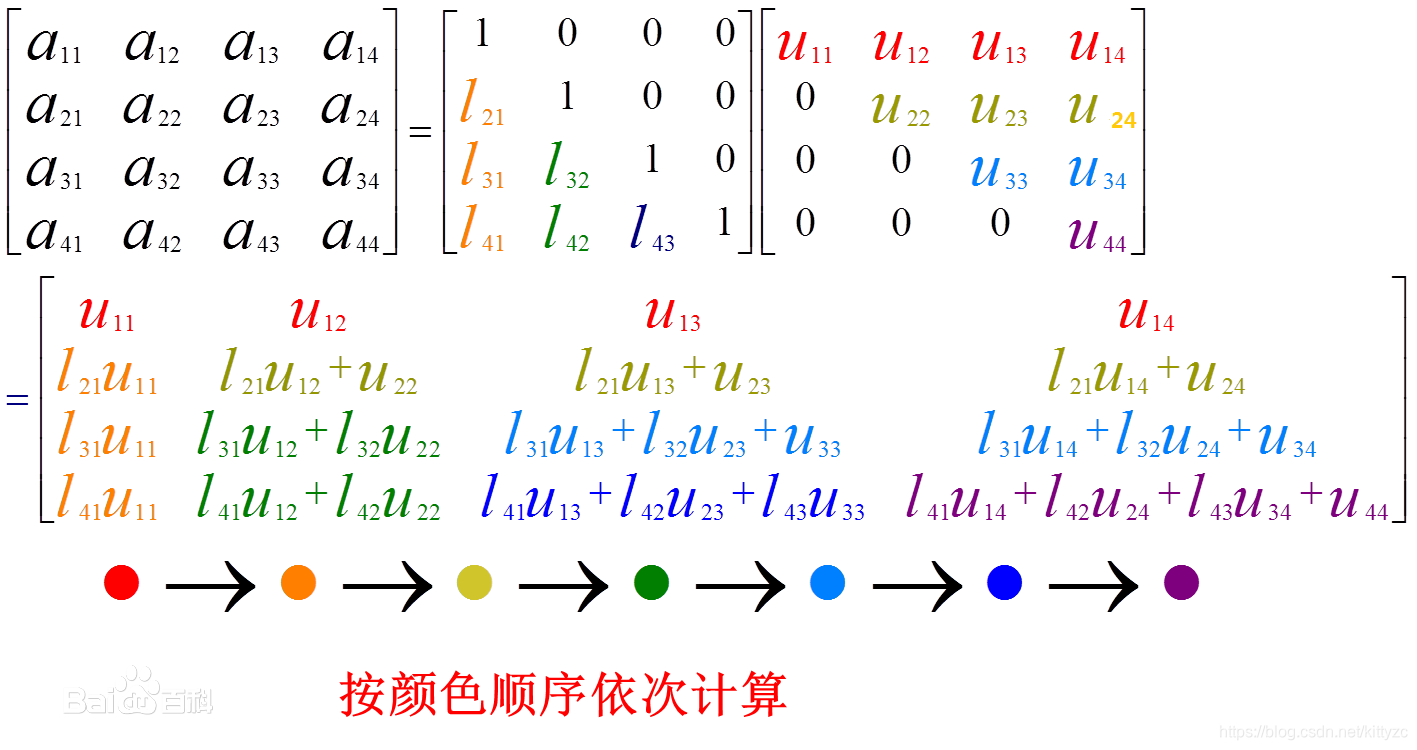
LU分解主要应用在数值分析中，用来解线性方程、求反矩阵或计算行列式，起源于高斯消元法，也即所谓的杜尔里特算法（Doolittle algorithm）：从下至上地对矩阵A做初等行变换，将对角线左下方的元素变成零，然后再证明这些行变换的效果等同于左乘一系列单位下三角矩阵，这一系列单位下三角矩阵的乘积的逆就是L矩阵，它也是一个单位下三角矩阵。

def LU(A):U = np.copy(A)m, n = A.shapeL = np.eye(n)for k in range(n-1):for j in range(k+1,n):L[j,k] = U[j,k]/U[k,k]U[j,k:n] -= L[j,k] * U[k,k:n]return L, U

2. 特征分解与SVD分解

直观理解，当A正定时，特征分解是求$\sqrt{A}$，而SVD分解是求$|B|$

奇异值分解起源于方阵的特征分解：$A=Q\Sigma Q^{-1}$，通过Q变换，所有维度之间变为相互独立，A矩阵的旋转和投影效应被消除。
对于非方阵，可以用奇异值分解：$B=U\Sigma V^T$，其中U和V都是正交阵。SVD的意义类似奇异值分解，但又有些不一样。SVD的右奇异向量(V的列向量)是$B^{T}B$的特征向量，它的左奇异向量(U的列向量)是$B{B}^T$的特征向量，而奇异值是这两个对称矩阵相同的非零特征值的平方根(实际上它们两个非零特征值一模一样)。
总结来说，特征值分解是针对$A$来的，而奇异值分解是针对$B{B}^T$来的（强制把非方阵变为了方阵）。奇异值计算量非常大，需要先计算$B{B}^T$和$B^{T}B$，然后用LU分解计算特征向量和特征值，N^3复杂度，规模大时计算量很大。

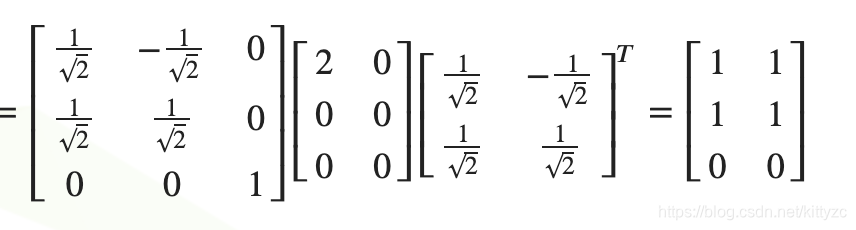
3. 逆矩阵

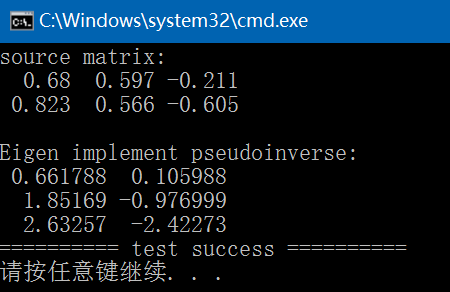
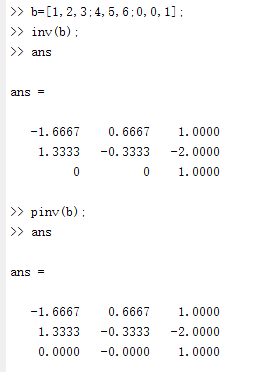
对于任何矩阵 A 来说，伪逆 B 都存在，是唯一的，并且具有与 A’ 相同的维度。如果 A 是方阵且非奇异，则 pinv(A) 只是一种成本比较高的计算 inv(A) 的方式。但是，如果 A 不是方阵，或者是方阵且奇异，则 inv(A) 不存在。在这些情况下，pinv(A) 拥有 inv(A) 的部分（但非全部）属性。

1、pinv 通过奇异值分解来形成 A 的伪逆。
2、inv 执行输入矩阵的 LU 分解（如果输入矩阵是 Hermitian 矩阵，则执行 LDL 分解）。然后它使用结果来形成线性方程组，其解为矩阵求逆 inv(X)。
3、如果是奇异矩阵，此时不存在逆矩阵，可用pinv(A)求其伪逆。
4、如果是非奇异矩阵，存在逆矩阵，可用inv(A)，也可用pinv(A),只不过pinv(A)的计算成本较高。

若$A=Q\Sigma Q^{-1}$，则$A^{-1}=Q(1/\Sigma )Q^{-1}$
若$B=U\Sigma V^T$，则$B^{-1}=V(1/\Sigma {)}^T{U}^T$