解释及实现

记$X$的伪逆为$pinv(X)$，则有
$pinv(X)=(X^{T}X{)}^{-1}{X}^T$，容易发现$pinv(X)X=I$
在numpy中可以使用numpy.linalg.pinv求伪逆。
例子：¹

>>> a = np.random.randn(9, 6)
>>> B = np.linalg.pinv(a)
>>> np.allclose(a, np.dot(a, np.dot(B, a)))
True
>>> np.allclose(B, np.dot(B, np.dot(a, B)))
True
>>> np.allclose(np.transpose(a), np.dot(B, np.dot(a, np.transpose(a))))
True

numpy.linalg.pinv只是numpy众多线性代数函数中的一个，了解更多numpy的线性代数方面的函数，可以看这个链接。

笔记

矩阵 $A$ 的伪逆矩阵，记为$A^{+}$ , 定义为：解决最小二乘问题的矩阵。例如， $Ax=b$ 的最小二乘解 $\hat{x}=A^{+}b$。

可以证明，如果 $Q_1\Sigma Q_2^T$ 是 $A$ 的奇异值分解，那么 $A^{+}=Q_2{\Sigma }^{+}{Q}_1^T$，其中， $Q_{1,2}$ 是正交矩阵， $\Sigma$ 是一个由 $A$ 的奇异值构成的对角矩阵，${\Sigma }^{+}$ 是由 A 的奇异值的倒数组成的对角矩阵。

伪逆在最简单的线性回归中的应用

最小二乘回归是最简单的线性回归，下边就用伪逆来计算一下最小二乘回归。并使用了sklearn中的最小二乘回归做对比，比较两者效率的高下。

import numpy as np
n = 9999999
x = np.arange(n)
np.random.seed(123)
y = x + 3 + np.random.standard_normal(n)# 使用伪逆来计算
import time as t
tic = t.time()
temp = np.ones(n).reshape(-1, 1)
x_aug = np.c_[temp, x]
pinv_x_aug = np.linalg.pinv(x_aug)  # 这个叫伪逆
b1, k1 = np.dot(pinv_x_aug, y)  # 第一个的是截距，第二个是斜率
toc = t.time()
cost_pinv = toc-tic# 使用sklearn的线性模型来计算
from sklearn import linear_model
tic = t.time()
reg = linear_model.LinearRegression()
reg.fit(x.reshape(-1, 1), y.reshape(-1, 1))
k2 = reg.coef_
b2 = reg.intercept_
toc = t.time()
cost_sklearn = toc-tic

计算结果截图如下

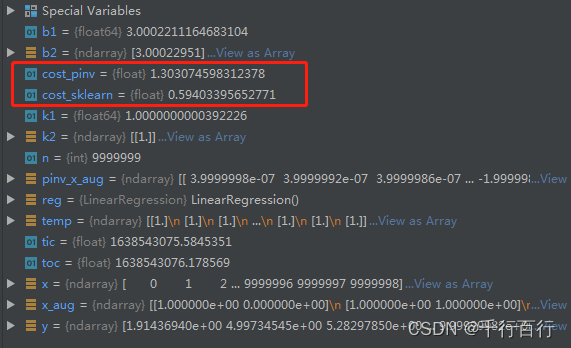
从结果中看出，两种方法计算得到的斜率和截距都是一样的。但是：

1. sklearn的耗时大概是使用伪逆方法的一半！

2. 可见sklearn还是厉害啊！没事就不要自己造轮子了。

---

1. SciPy官方：numpy.linalg.pinv ↩︎