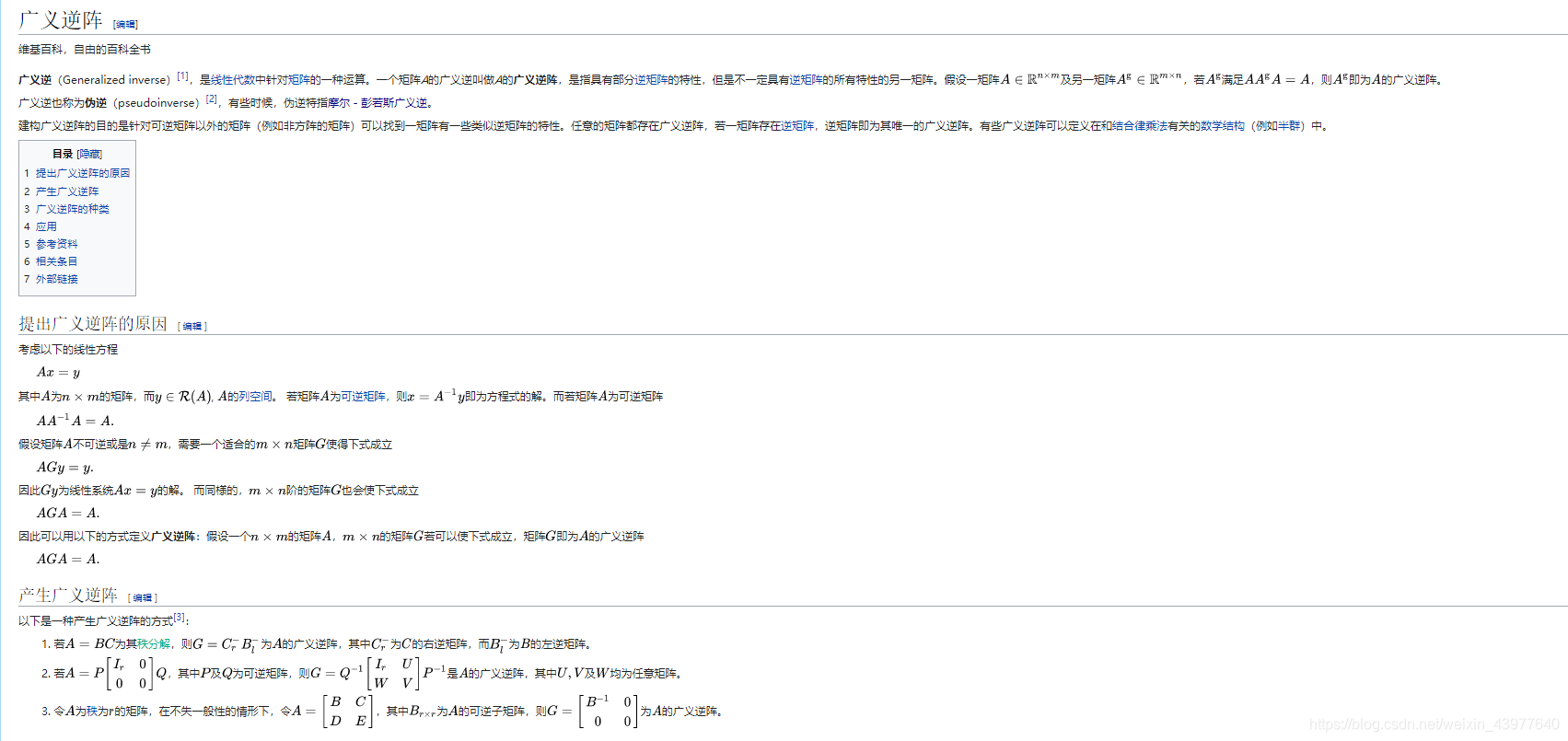
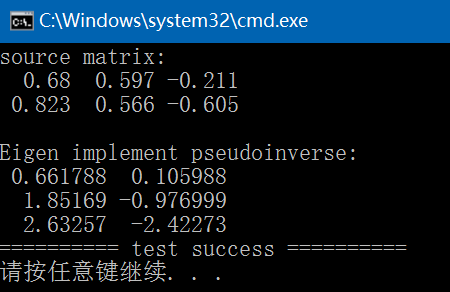
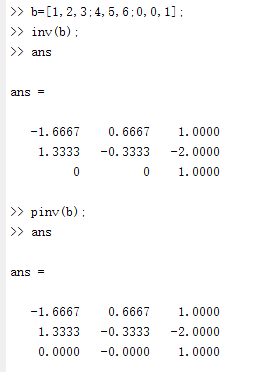
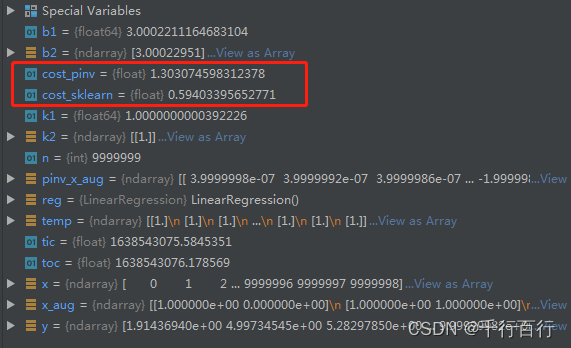
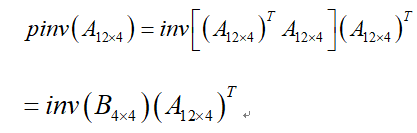inv是求矩阵A的逆矩阵,pinv是求矩阵A的伪逆矩阵
import numpy as npa = np.array([[1, 0, 0],[0, 6, 0],[0, 0, 9]])
print('\n', np.linalg.inv(a)) # 求逆矩阵
print('\n', np.linalg.pinv(a)) # 求伪逆矩阵,当本身就可逆的时候,二者结果相同b = np.array([[1, 4, 1, 5]])
print('\n', np.linalg.pinv(b))
print('\n', b @ np.linalg.pinv(b)) # 可以看到伪逆矩阵的性质还是使它们俩相乘为E
逆矩阵概念:设A是一个n阶矩阵,若存在另一个n阶矩阵B,使得: AB=BA=E ,则称方阵A可逆,并称方阵B是A的逆矩阵
不是所有的矩阵都存在逆矩阵的,但有时候不得不用到,举个例子:
,则:
当A可逆的时候完全没问题,但是当A不可逆的时候只能用pinv求伪逆矩阵,照样能得到结果,但是存在一定的误差,不能忽略