一、pinv()原型
函数形式:pinv(J, G, P);
核心算法: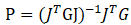
解释:G是正定矩阵,P是矩阵J的伪逆矩阵。当G为恒定常数时,以下等式成立:
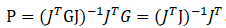
函数原型:
template<typename DerivedA, typename DerivedB, typename DerivedC>
void pinv(const MatrixBase<DerivedA>& J, const MatrixBase<DerivedB>&G, MatrixBase<DerivedC>& P)
{MatrixXd J_temp(2, 2);J_temp = J.transpose()*G*J;P = (A_temp.inverse())*J.transpose()*G;
}
二、验证上述等式
直接上代码:
template<typename DerivedA, typename DerivedB, typename DerivedC>
void pinv(const MatrixBase<DerivedA>& A, const MatrixBase<DerivedB>&G, MatrixBase<DerivedC>& B)
{//这里就是在算这个投影矩阵p,最后的结果用B输出来,这里的A就是那个Γ,这里的G就是那个GMatrixXd A_temp(2, 2);A_temp = A.transpose()*G*A;B = (A_temp.inverse())*A.transpose()*G;}template<typename DerivedA, typename DerivedB>
void pinv2(const MatrixBase<DerivedA>& A, MatrixBase<DerivedB>& B) {MatrixXd A_temp(2, 2);A_temp = A.transpose()*A;B = (A_temp.inverse())*A.transpose();
}int main()
{Vector2d ratio;Matrix3d m_ratio;MatrixXd projection(2, 3);MatrixXd a(3, 2); a<< 3, 0,88, 0,0, 1;pinv2(a, projection);// 求a的伪逆矩阵projectioncout << "projection = " << endl << projection << endl << endl;/*** 验证当G为任意常数时,pinv()等价于pinv2() **************************************/MatrixXd projection2(2, 3);Matrix2d G;G << 5, 0,0,5,; pinv(a, G, projection2);cout << "projection2 = " << endl << projection2 << endl;
}
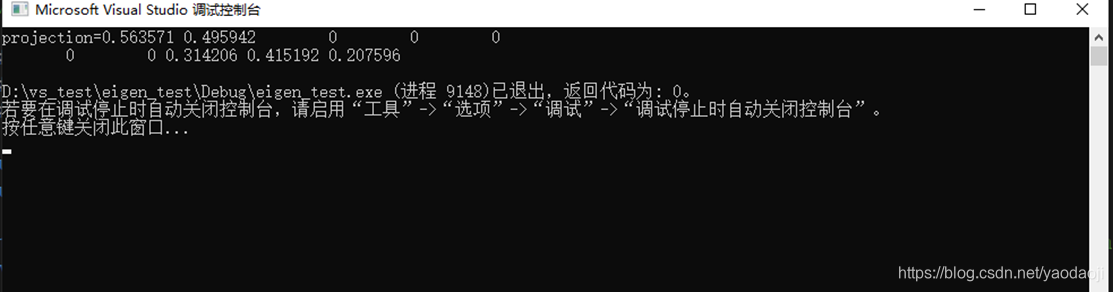
打印结果如下:
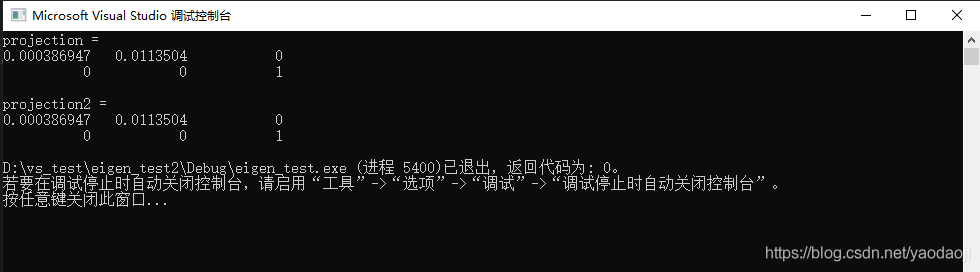
当我们改变G是值的时候,打印结果依然不变,可以证明:
当G为恒定常数时,
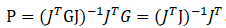
三、上述pinv()算法是否与Matlab中的pinv()函数一样?
思路:我们以求b矩阵的伪逆矩阵为例,看看与在Matlab中调用pinv()所得结果是否一致。
b << 1, 2, 3,4, 5, 6,0, 0, 1;
(1)首先利用我们前面介绍的算法,看看结果如何:
int main()
{MatrixXd projection3(3, 3);MatrixXd projection4(3, 3);MatrixXd b(3, 3); Matrix3d G;G<< 50, 0,0,0,50, 0,0, 0, 50; b << 1, 2, 3,4, 5, 6,0, 0, 1;pinv2(b, projection3);pinv(b, G, projection4);cout << "projection3 = " << endl << projection3 << endl << endl;cout << "projection4 = " << endl << projection4 << endl;cout << "b.inverse() = " << endl << b.inverse() << endl;
}
我们顺便把b的逆矩阵也求出来了,结果为:
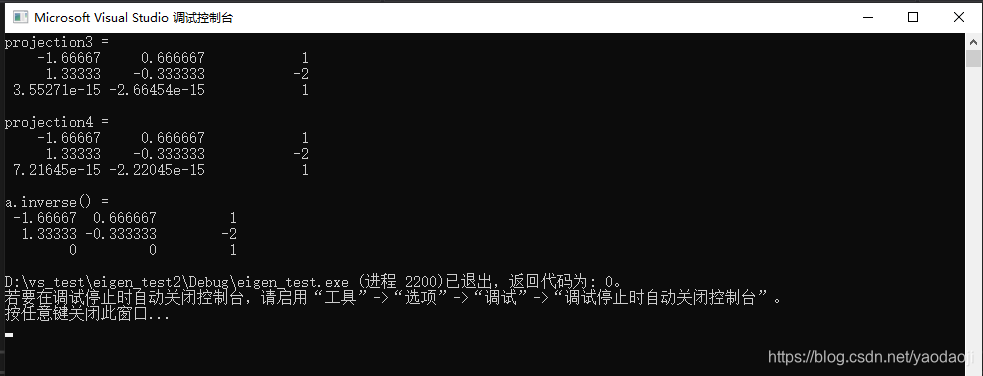
可以发现伪逆矩阵和逆矩阵结果是一样的。
(2)再看看在Matlab中的计算结果:
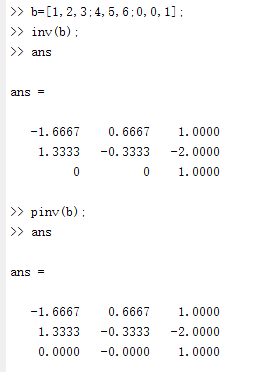
(3)结论
【1】可以发现Matlab计算出来的pinv(b)与前面的算法计算的结果一样。
所以,可以得出,我们写的pinv()函数与Matlab调用的pinv()是一样的。
【2】我们还可以发现,伪逆矩阵和逆矩阵也相同。有这样的一个结论:
当A矩阵是方阵,且可逆时,A的伪逆矩阵=A的逆矩阵。