numpy中求矩阵的逆与伪逆

numpy中求矩阵的逆：numpy.linalg.inv()
numpy中求矩阵的伪逆: numpy.linalg.pinv()

numpy中求矩阵的逆（numpy.linalg.inv)

使用命令numpy.linalg.inv(Matrix)

功能

Compute the (multiplicative) inverse of a matrix.
Given a square matrix a, return the matrix ainv satisfying
dot(a, ainv) = dot(ainv, a) = eye(a.shape[0]).

计算一个方阵的逆，使之满足$A{A}^{-1}=A^{-1}A=I$

Parameters

• a : (…, M, M) array_like
  Matrix to be inverted.

a是输入的要计算逆的矩阵数组。

Returns

• ainv : (…, M, M)
  ndarray or matrix (Multiplicative) inverse of the matrix a.

返回的是对应的逆矩阵的数组。

Raises

• LinAlgError
  If a is not square or inversion fails.

如果a不是方阵或者不可逆，则Raise LinAlgError

Examples

>>> from numpy.linalg import inv
>>> a = np.array([[1., 2.], [3., 4.]])
>>> ainv = inv(a)
>>> np.allclose(np.dot(a, ainv), np.eye(2))
True
>>> np.allclose(np.dot(ainv, a), np.eye(2))
TrueIf a is a matrix object, then the return value is a matrix as well:>>> ainv = inv(np.matrix(a))
>>> ainv
matrix([[-2. ,  1. ],[ 1.5, -0.5]])Inverses of several matrices can be computed at once:>>> a = np.array([[[1., 2.], [3., 4.]], [[1, 3], [3, 5]]])
>>> inv(a)
array([[[-2.  ,  1.  ],[ 1.5 , -0.5 ]],[[-1.25,  0.75],[ 0.75, -0.25]]])

numpy中求矩阵的伪逆(numpy.linalg.inv)

伪逆的定义以及意义

伪逆在某些情况下特指摩尔彭若斯广义逆。
广义逆矩阵：

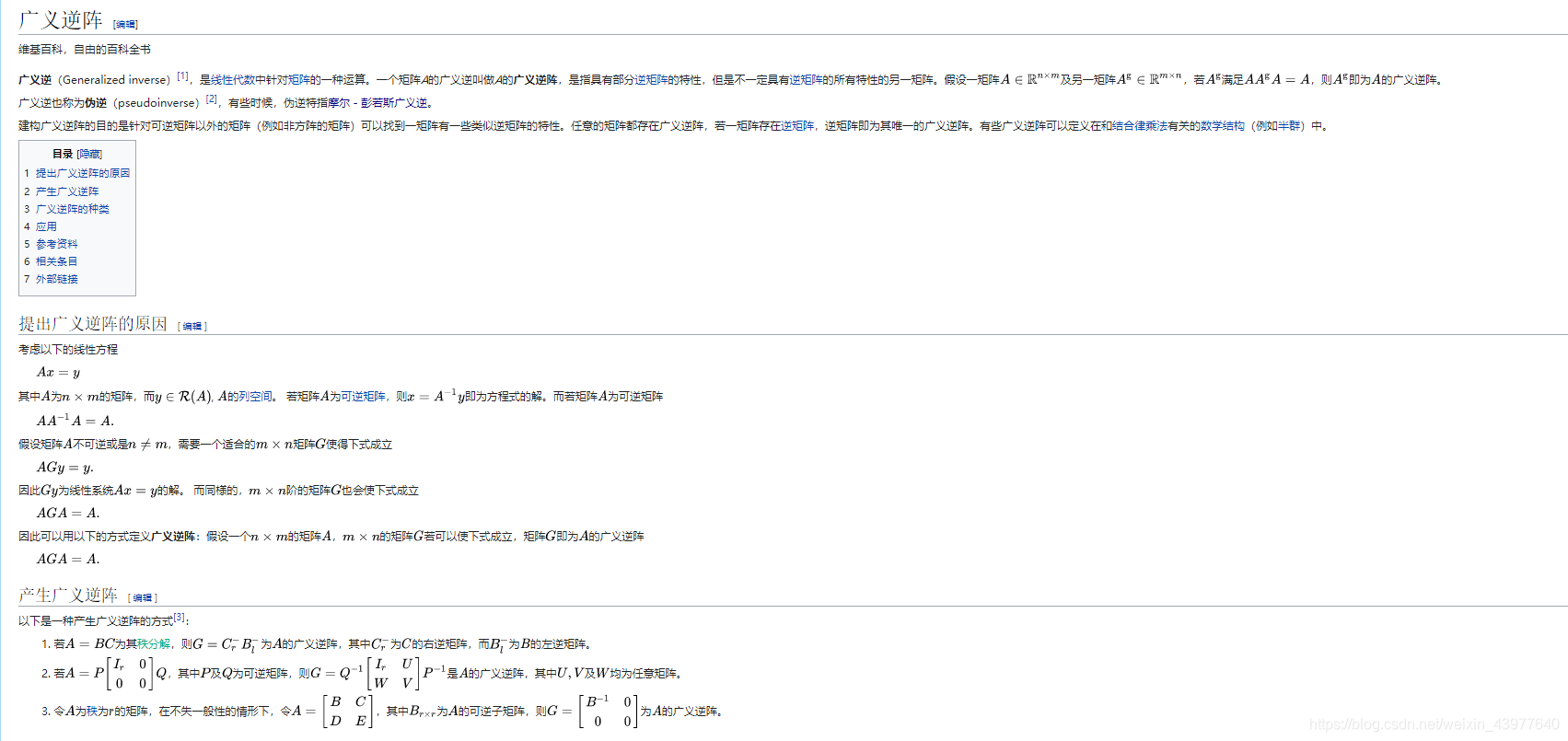
$A$的摩尔彭若斯矩阵记为$A^{+}$.那么有两个基本性质：

$$A{A}^{+}A=A$$

$$A^{+}A{A}^{+}=A^{+}$$

功能

Compute the (Moore-Penrose) pseudo-inverse of a matrix.
Calculate the generalized inverse of a matrix using its singular-value decomposition (SVD) and including all large singular values.
… versionchanged:: 1.14
Can now operate on stacks of matrices

Parameters

• a : (…, M, N) array_like

Matrix or stack of matrices to be pseudo-inverted.

要做伪逆运算的矩阵或者矩阵的栈

• rcond : (…) array_like of float

Cutoff for small singular values.
Singular values less than or equal to rcond * largest_singular_value are set to zero.
Broadcasts against the stack of matrices.

对很小的奇异值做裁剪。当某个奇异值小于等于最大的奇异值乘以rcond，就将它设置为0.

• hermitian : bool, optional

If True, a is assumed to be Hermitian (symmetric if real-valued),
enabling a more efficient method for finding singular values.
Defaults to False.

如果为真，相当于告诉Numpy输入矩阵是Hermitian矩阵。会采用更加有效的方法去寻找奇异值。默认为False.

Returns

• B : (…, N, M) ndarray

The pseudo-inverse of a. If a is a matrix instance, then so is B.

返回a的伪逆

Raises

• LinAlgError

If the SVD computation does not converge.

如果矩阵不能进行奇异值分解(SVD)，则报错。

See Also

--------
scipy.linalg.pinv : Similar function in SciPy.
scipy.linalg.pinv2 : Similar function in SciPy (SVD-based).
scipy.linalg.pinvh : Compute the (Moore-Penrose) pseudo-inverse of aHermitian matrix.

Notes

The pseudo-inverse of a matrix A, denoted $A^{+}$, is
defined as: “the matrix that ‘solves’ [the least-squares problem]
$Ax=b$,” i.e., if $\bar{x}$ is said solution, then $A^{+}$ is that matrix such that $\bar{x}=A^{+}b$.

It can be shown that if : $Q_1\Sigma Q_2^T=A$ is the singular value decomposition of A, then $A^{+}=Q_2{\Sigma }^{+}{Q}_1^T$, where :$Q_{1,2}$ are orthogonal matrices, :$\Sigma$ is a diagonal matrix consisting of A’ s so-called singular values, (followed, typically, by zeros), and then :${\Sigma }^{+}$ is simply the diagonal matrix consisting of the reciprocals of A’s singular values (again, followed by zeros).
References:
… [1] G. Strang, Linear Algebra and Its Applications, 2nd Ed., Orlando,
FL, Academic Press, Inc., 1980, pp. 139-142.

对于矩阵A，有方程$Ax=b$,那么它的摩尔彭若斯伪逆$A^{+}$满足：对于$\bar{x}=A^{+}b$, $\bar{x}$能使得$Ax$与$b$的二范数距离最小。
矩阵A的摩尔彭若斯伪逆可以通过奇异值分解来求得。A的奇异值分解为：$Q_1\Sigma Q_2^T=A$。那么其伪逆$A^{+}=Q_2{\Sigma }^{+}{Q}_1^T$。其中${\Sigma }^{+}$就是$\Sigma$的对角元素的倒数构成的对角矩阵。其实因为$\Sigma$本身就是对角矩阵，${\Sigma }^{+}$就是${\Sigma }^{-1}$

Examples

The following example checks that a * a+ * a == a and
a+ * a * a+ == a+:

>>> a = np.random.randn(9, 6)
>>> B = np.linalg.pinv(a)
>>> np.allclose(a, np.dot(a, np.dot(B, a)))
True
>>> np.allclose(B, np.dot(B, np.dot(a, B)))
True

---

如果觉得文章对您有帮助的话，可以点个赞，是对博主最大的肯定！