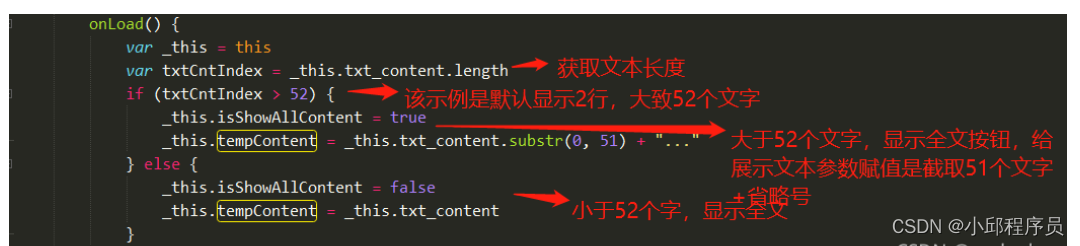
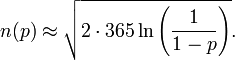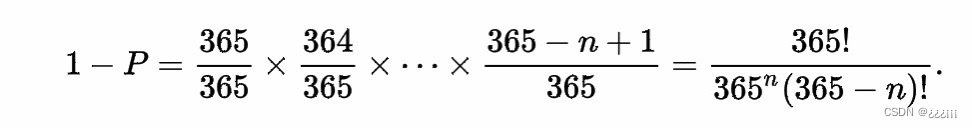上篇文章 洗牌算法详解 讲到了验证概率算法的蒙特卡罗方法,今天聊点轻松的内容:几个和概率相关的有趣问题。
计算概率有下面两个最简单的原则:
原则一、计算概率一定要有一个参照系,称作「样本空间」,即随机事件可能出现的所有结果。事件 A 发生的概率 = A 包含的样本点 / 样本空间的样本总数。
原则二、计算概率一定要明白,概率是一个连续的整体,不可以把连续的概率分割开,也就是所谓的条件概率。
上述两个原则高中就学过,但是我们还是很容易犯错,而且犯错的流程也有异曲同工之妙:
先是忽略了原则二,错误地计算了样本空间,然后通过原则一算出了错误的答案。
下面介绍几个简单却具有迷惑性的问题,分别是男孩女孩问题、生日悖论、三门问题。当然,三门问题可能是大家最耳熟的,所以就多说一些有趣的思考。
一、男孩女孩问题
假设有一个家庭,有两个孩子,现在告诉你其中有一个男孩,请问另一个也是男孩的概率是多少?
很多人,包括我在内,不假思索地回答:1/2 啊,因为另一个孩子要么是男孩,要么是女孩,而且概率相等呀。但是实际上,答案是 1/3。
上述思想为什么错误呢?因为没有正确计算样本空间,导致原则一计算错误。有两个孩子,那么样本空间为 4,即哥哥妹妹,哥哥弟弟,姐姐妹妹,姐姐弟弟这四种情况。已知有一个男孩,那么排除姐姐妹妹这种情况,所以样本空间变成 3。另一个孩子也是男孩只有哥哥弟弟这 1 种情况,所以概率为 1/3。
为什么计算样本空间会出错呢?因为我们忽略了条件概率,即混淆了下面两个问题:
这个家庭只有一个孩子,这个孩子是男孩的概率是多少?
这个家庭有两个孩子,其中一个是男孩,另一个孩子是男孩的概率是多少?
根据原则二,概率问题是连续的,不可以把上述两个问题混淆。第二个问题需要用条件概率,即求一个孩子是男孩的条件下,另一个也是男孩的概率。运用条件概率的公式也很好算,就不多说了。
通过这个问题,读者应该理解两个概率计算原则的关系了,最具有迷惑性的就是条件概率的忽视。为了不要被迷惑,最简单的办法就是把所有可能结果穷举出来。
最后,对于此问题我见过一个很奇葩的质疑:如果这两个孩子是双胞胎,不存在年龄上的差异怎么办?
我竟然觉得有那么一丝道理!但其实,我们只是通过年龄差异来表示两个孩子的独立性,也就是说即便两个孩子同性,也有两种可能。所以不要用双胞胎抬杠了。
二、生日悖论
生日悖论是由这样一个问题引出的:一个屋子里需要有多少人,才能使得存在至少两个人生日是同一天的概率达到 50%?
答案是 23 个人,也就是说房子里如果有 23 个人,那么就有 50% 的概率会存在两个人生日相同。这个结论看起来不可思议,所以被称为悖论。按照直觉,要得到 50% 的概率,起码得有 183 个人吧,因为一年有 365 天呀?其实不是的,觉得这个结论不可思议主要有两个思维误区:
第一个误区是误解「存在」这个词的含义。
读者可能认为,如果 23 个人中出现相同生日的概率就能达到 50%,是不是意味着:
假设现在屋子里坐着 22 个人,然后我走进去,那么有 50% 的概率我可以找到一个人和我生日相同。但这怎么可能呢?
并不是的,你这种想法是以自我为中心,而题目的概率是在描述整体。也就是说「存在」的含义是指 23 人中的任意两个人,涉及排列组合,大概率和你没啥关系。
如果你非要计算存在和自己生日相同的人的概率是多少,可以这样计算:
1 - P(22 个人都和我的生日不同) = 1 -(364/365)^22 = 0.06
这样计算得到的结果是不是看起来合理多了?生日悖论计算对象的不是某一个人,而是一个整体,其中包含了所有人的排列组合,它们的概率之和当然会大得多。
第二个误区是认为概率是线性变化的。
读者可能认为,如果 23 个人中出现相同生日的概率就能达到 50%,是不是意味着 46 个人的概率就能达到 100%?
不是的,就像中奖率 50% 的游戏,你玩两次的中奖率就是 100% 吗?显然不是,你玩两次的中奖率是 75%:
$P(两次能中奖) = P(第一次就中了) + P(第一次没中但第二次中了) = 1/2 + 1/2*1/2 = 75\%$
那么换到生日悖论也是一个道理,概率不是简单叠加,而要考虑一个连续的过程,所以这个结论并没有什么不合常理之处。
那为什么只要 23 个人出现相同生日的概率就能大于 50% 了呢?我们先计算 23 个人生日都唯一(不重复)的概率。只有 1 个人的时候,生日唯一的概率是 $365/365$,2 个人时,生日唯一的概率是 $365/365 × 364/365$,以此类推可知 23 人的生日都唯一的概率:
算出来大约是 0.493,所以存在相同生日的概率就是 0.507,差不多就是 50% 了。实际上,按照这个算法,当人数达到 70 时,存在两个人生日相同的概率就上升到了 99.9%,基本可以认为是 100% 了。所以从概率上说,一个几十人的小团体中存在生日相同的人真没啥稀奇的。
三、三门问题
这个游戏很经典了:游戏参与者面对三扇门,其中两扇门后面是山羊,一扇门后面是跑车。参与者只要随便选一扇门,门后面的东西就归他(跑车的价值当然更大)。但是主持人决定帮一下参与者:在他选择之后,先不急着打开这扇门,而是由主持人打开剩下两扇门中的一扇,展示其中的山羊(主持人知道每扇门后面是什么),然后给参与者一次换门的机会,此时参与者应该换门还是不换门呢?
为了防止第一次看到这个问题的读者迷惑,再具体描述一下这个问题:
你是游戏参与者,现在有门 1,2,3,假设你随机选择了门 1,然后主持人打开了门 3 告诉你那后面是山羊。现在,你是坚持你最初的选择门 1,还是选择换成门 2 呢?
答案是应该换门,换门之后抽到跑车的概率是 2/3,不换的话是 1/3。又一次反直觉,感觉换不换的中奖概率应该都一样啊,因为最后肯定就剩两个门,一个是羊,一个是跑车,这是事实,所以不管选哪个的概率不都是 1/2 吗?
类似前面说的男孩女孩问题,最简单稳妥的方法就是把所有可能结果穷举出来:

很容易看到选择换门中奖的概率是 2/3,不换的话是 1/3。
关于这个问题还有更简单的方法:主持人开门实际上在「浓缩」概率。一开始你选择到跑车的概率当然是 1/3,剩下两个门中包含跑车的概率当然是 2/3,这没啥可说的。但是主持人帮你排除了一个含有山羊的门,相当于把那 2/3 的概率浓缩到了剩下的这一扇门上。那么,你说你是抱着原来那扇 1/3 的门,还是换成那扇经过「浓缩」的 2/3 概率的门呢?
再直观一点,假设你三选一,剩下 2 扇门,再给你加入 98 扇装山羊的门,把这 100 扇门随机打乱,问你换不换?肯定不换对吧,这明摆着把概率稀释了,肯定抱着原来的那扇门是最可能中跑车的。再假设,初始有 100 扇门,你选了一扇,然后主持人在剩下 99 扇门中帮你排除 98 个山羊,问你换不换一扇门?肯定换对吧,你手上那扇门是 1%,另一扇门是 99%,或者也可以这样理解,不换只是选择了 1 扇门,换门相当于选择了 99 扇门,这样结果很明显了吧?
以上思想,也许有的读者都思考过,下面我们思考这样一个问题:假设你在决定是否换门的时候,小明破门而入,要求帮你做出选择。他完全不知道之前发生的事,他只知道面前有两扇门,一扇是跑车一扇是山羊,那么他抽中跑车的概率是多大?
当然是 1/2,这也是很多人做错三门问题的根本原因。类似生日悖论,人们总是容易以自我为中心,通过这个小明的视角来计算是否换门,这显然会进入误区。
就好比有两个箱子,一号箱子有 4 个黑球 2 个红球,二号箱子有 2 个黑球 4 个红球,随便选一个箱子,随便摸一个球,问你摸出红球的概率。
对于不知情的小明,他会随机选择一个箱子,随机摸球,摸到红球的概率是:1/2 × 2/6 + 1/2 × 4/6 = 1/2
对于知情的你,你知道在二号箱子摸球概率大,所以只在二号箱摸,摸到红球的概率是:0 × 2/6 + 1 × 4/6 = 2/3
三门问题是有指导意义的。比如你蒙选择题,先蒙了 A,后来灵机一动排除了 B 和 C,请问你是否要把 A 换成 D?答案是,换!
也许读者会问,如果只排除了一个答案,比如说 B,那么我是否应该把 A 换成 C 或者 D 呢?答案是,换!
因为按照刚才「浓缩」概率这个思想,只要进行了排除,都是在进行「浓缩」,均摊下来肯定比你一开始蒙的那个答案概率 1/4 高。比如刚才的例子,C 和 D 的正确概率都是 3/8,而你开始蒙的 A 只有 1/4。
当然,运用此策略蒙题的前提是你真的抓瞎,真的随机乱选答案,这样概率才能作为最后的杀手锏。
_____________
公众号:labuladong
B站:labuladong
知乎:labuladong
From https://labuladong.github.io/ebook/%E7%AE%97%E6%B3%95%E6%80%9D%E7%BB%B4%E7%B3%BB%E5%88%97/%E5%87%A0%E4%B8%AA%E5%8F%8D%E7%9B%B4%E8%A7%89%E7%9A%84%E6%A6%82%E7%8E%87%E9%97%AE%E9%A2%98.html