python生日悖论分析
If you have a group of people in a room, how many do you need to for it to be more likely than not, that two or more will have the same birthday?
如果您在一个房间里有一群人,那么您需要多少个才能使两个或两个以上的人有相同的生日?
Theoretically, the chances of two people having the same birthday are 1 in 365 (not accounting for leap years and the uneven distribution of birthdays across the year), and so odds are you’ll only meet a handful of people in your life who enjoy the same birthday as you. This leads many people to intuitively guess around 180.
从理论上讲,两个人拥有相同生日的机会是365分之一(不考虑leap年和全年中生日分布不均),因此,您人生中只会遇到少数几个喜欢和你一样的生日 这导致许多人凭直觉猜测大约180。
The correct answer is just 23.
正确的答案只有23。
That means in each of your classes at school, amongst the fellow commuters on the bus to work and amongst the players on a soccer field, there are more than likely at least two people with the same birthday.
这意味着在您学校的每个班级中,上班的通勤同胞和足球场上的球员中,至少有两个人的生日相同。
Humans have a notoriously poor intuition when it comes to probability. The multi-billion dollar gambling industry is proof of this.
当涉及到概率时,人类的直觉非常差。 数十亿美元的赌博业就是证明。
The source of confusion within the Birthday Paradox is that the probability grows relative to the number of possible pairings of people, not just the group’s size. The number of pairings grows with respect to the square of the number of participants, such that a group of 23 people contains 253 (23 x 22 / 2) unique pairs of people.
生日悖论之内的困惑根源在于,这种可能性相对于可能的配对人数而增加,而不仅仅是小组的人数。 配对的数量相对于参与者数量的平方而增加,因此,一个23人的组包含253(23 x 22/2)个独特的人对。
In each of these pairings, there is a 364/365 chance of having different birthdays, but this needs to happen for every pair for there to be no matching birthdays across the entire group. Therefore the probability of two people having the same birthday in a group of 23 is:
在每个配对中,都有364/365个不同生日的机会,但是每对配对都需要这样做,因为整个组中没有匹配的生日。 因此,在23人一组中,两个人有相同生日的概率为:
1 — (364/365)^253 = 50.05%If we plot the probability vs different group sizes, we see how the probability grows as the group size increases.
如果我们绘制概率与不同组大小的关系图,我们将看到概率随着组大小的增加而增加。
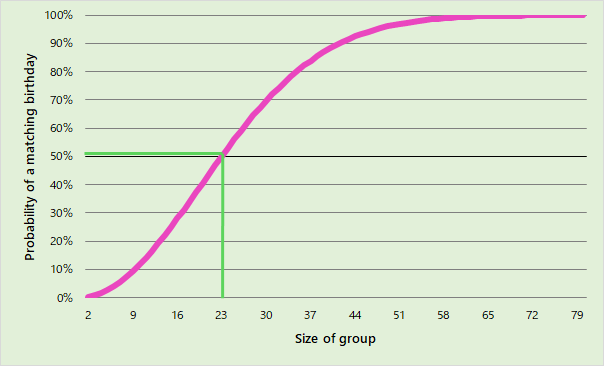
The line crosses 50% just before a group size of 23. Our previous guess of 180 has a probability so close to 100%, it’s not worth showing. In fact, the chance of choosing a group of 180 people at random, and having none of them share the same birthday, is roughly 6x10^-20 — 100 times less likely than two people picking the same grain of sand out of all the sand on Earth!
这条线在小组人数23之前越过了50%。我们先前的180猜测很可能接近100%,因此不值得显示。 实际上,随机选择一组180个人并且没有一个人共享同一生日的机会大约是6x10 ^ -20-比两个人从所有沙子中挑选相同颗粒的可能性低100倍在地球上!
不太可能的巧合 (Less likely coincidences)
We can generalise the Birthday Paradox to look at other phenomena with a similar structure.
我们可以概括生日悖论,以研究具有相似结构的其他现象。
The probability of two people having the same PIN on their bank card is 1 in 10,000, or 0.01%. It would only take a group of 119 people however, to have odds in favour of two people having the same PIN.
两个人的银行卡上具有相同PIN的概率为10,000分之一,即0.01%。 但是,只需要一组119人,就能使两个人拥有相同的PIN。
Of course, these numbers assume a randomly sampled, uniform distribution of birthdays and PINs. In reality, birthdays peak at certain times of year and people are more likely to pick certain numbers than others for their PIN. But the lack of a uniform distribution in fact reduces the size of group that you need.
当然,这些数字假设生日和PIN是随机抽样的均匀分布。 实际上, 生日会在一年中的某些时候达到顶峰 ,因此人们选择PIN的可能性比其他人高。 但是实际上缺乏统一的分布会减小所需组的大小。
If we decrease the probability of a coincidence occurring, the size of group required to get an even chance of a collision obviously increases. However, it increases much more slowly than inverse of the probability.
如果我们降低发生重合的可能性,则获得均匀碰撞机会所需的组的大小会明显增加。 但是,它的增长比概率倒数慢得多。
For example, with a probability of 1 in 10,000, the minimum group size is 119. For a coincidence 10x less likely, the minimum group is 373, or only 3.15 times bigger. Therefore, even for incredibly tiny probabilities, the group size doesn’t grow particularly large. For odds of one in a million, the group required is only 1178.
例如,概率为10,000分之一,最小组大小为119。如果巧合的可能性小10倍,则最小组为373,或仅大3.15倍。 因此,即使对于极小的概率,组的大小也不会特别大。 对于百万分之一的赔率,所需的小组仅为1178。
宇宙垃圾 (Space junk)

This has implications in the area of satellite collisions and space junk. The odds of two particular orbiting objects colliding with each other over the course of a year are almost infinitesimally small. However, given that there are around 5,500 satellites and approximately 900,000 objects of greater than 1 cm in size whizzing above our heads, collisions occur more regularly than you might expect.
这在卫星碰撞和太空垃圾领域具有影响。 在一年的过程中,两个特定的轨道物体相互碰撞的几率几乎是无限小。 但是,考虑到大约有5500颗卫星和大约900,000个大小超过1厘米的物体在我们头顶上方呼啸而过,因此发生碰撞的次数比您预期的要多。
Various governments are able to track the larger pieces of space junk. This allows avoidance manoeuvres to take place to shift active satellites and the space station out of harm’s way. But with around 20,000 close approaches per week and growing, this could become an increasingly difficult and costly procedure.
各国政府能够追踪更大的太空垃圾。 这样可以进行回避演习,以使活动中的卫星和空间站摆脱伤害。 但是,随着每周大约20,000种接近方法不断发展,这可能会变得越来越困难且成本更高。
In 2009, two satellites — an 16 year old defunct Russian military satellite and a still active Iridium communications satellite — collided, at a relative velocity of almost 12 km /s. Both satellites shattered into clouds of debris fragments, with over 1,000 pieces larger than a grapefruit in size.
2009年,两颗卫星以近12 km / s的相对速度相撞,这是一颗16岁的已经失效的俄罗斯军事卫星和一颗仍在活动的铱通信卫星。 两颗卫星都破碎成碎片碎片云,其大小比葡萄柚大1,000颗。
More space junk means a higher chance of collisions occurring. And each collision increases the number of pieces of space junk. This positive feedback loop, if it exceeds the rate at which objects fall into the atmosphere and burn up, could lead to something called the Kessler Syndrome. This is a chain reaction in which collisions become increasingly common, spraying out more and more debris, until placing a satellite in low earth orbit becomes too dangerous to be feasible.
更多的太空垃圾意味着发生碰撞的机会更高。 每次碰撞都会增加太空垃圾的数量。 这种正反馈回路如果超过物体掉入大气并燃烧的速率,则可能导致凯斯勒综合症。 这是一个连锁React,其中碰撞变得越来越普遍,喷出越来越多的碎片,直到将卫星置于低地球轨道变得太危险以致于无法实现。
DNA证据 (DNA evidence)
Over the past forty years, DNA evidence has revolutionised the field of forensic investigation. As we go about our daily business, we leave behind us a trail of genetic material, mostly via skin cells and hair. Governments compile huge databases of DNA “profiles”, recording a series of uncorrelated genetic markers.
在过去的四十年中,DNA证据彻底革新了法医调查领域。 在进行日常业务时,我们会留下大量遗传物质,主要是通过皮肤细胞和头发。 各国政府汇编了庞大的DNA“特征”数据库,记录了一系列不相关的遗传标记。
For some systems, the probability of two people matching on all recorded genetic markers is estimated at one in one trillion (excluding identical twins). Given this number is over 100x the number of people on the planet, if a person’s DNA is found at the scene, you can be pretty sure they were there, right?
对于某些系统,两个人在所有记录的遗传标记上匹配的概率估计为万亿分之一(不包括同卵双胞胎)。 鉴于这个数字是地球上人数的100倍以上,如果在现场发现一个人的DNA,您就可以确定他们在那里。
Well, not necessarily. Following on from the previous examples, a tiny probability can inflate into something tangible when you have a large enough group of people.
好吧,不一定。 在前面的示例之后,当您有足够多的人时,很小的概率就会膨胀为有形的东西。
In a country the size of the US (328 million people), a match rate of one in a trillion converts to a 1 in 3,000 chance of you having a genetic profile ‘twin’, somewhere out there. In 2019, there were 16k murders in the US. This means there are likely around 5 murders per year, for which the perpetrator’s DNA matches perfectly with that of another American (again, excluding identical twins). Even with the incredibly low probabilities involved, the power of the Birthday Paradox means that you shouldn’t convict based on DNA evidence alone, and other circumstantial evidence needs to be taken into consideration as well.
在美国这个庞大的国家(3.28亿人口)中,万亿分之一的匹配率可以使您在某处具有“双胞胎”遗传特征的概率为3,000的三分之一。 2019年,美国发生了1.6万起谋杀案。 这意味着每年可能有大约5起谋杀案,凶手的DNA与另一名美国人的DNA完全匹配(同样,不包括同卵双胞胎)。 即使涉及到的概率极低,“生日悖论”的力量也意味着您不应该仅凭DNA证据就定罪,还需要考虑其他间接证据。
It’s worth considering also, that DNA profiling systems have improved greatly in the last thirty years. Earlier in the application of the technology, probabilities of 1 in a billion were often quoted. This would have given around 5,000 murders with a DNA ambiguity.
同样值得考虑的是,在过去的30年中,DNA分析系统已经有了很大的进步。 在该技术的早期应用中,经常引用十亿分之一的概率。 这样一来,大约有5,000起谋杀案带有DNA歧义。
生日袭击 (Birthday Attack)

The Birthday Paradox can be leveraged in a cryptographic attack on digital signatures. Digital signatures rely on something called a hash function f(x), which transforms a message or document into a very large number (hash value). This number is then combined with the signer’s secret key to create a signature. Someone reading the document could then “de-crypt” the signature using the signer’s public key, and this would prove that the signer had digitally signed the document.
可以将生日悖论用于对数字签名的加密攻击。 数字签名依赖某种称为哈希函数 f(x)的函数 ,该函数将消息或文档转换为非常大的数字(哈希值) 。 然后将此数字与签名者的秘密密钥结合在一起以创建签名。 然后,阅读文档的人可以使用签名者的公钥“解密”签名,这将证明签名者已经对文档进行了数字签名。
These signatures can be used to verify the authenticity of a document. By reading this article on Medium.com, you’re using a digital signature right now, via the HTTPS protocol. The security relies on the difficulty of finding another document with the same hash value as the signed original.
这些签名可用于验证文档的真实性。 通过在Medium.com上阅读本文,您现在正在通过HTTPS协议使用数字签名。 安全性依赖于查找具有与签名原始文档相同的哈希值的另一个文档的难度。
However, the Birthday Paradox lets us potentially abuse this system by attacking this hash function.
但是,生日悖论使我们有可能通过攻击此哈希函数来滥用此系统。
Let’s say Bob is an authority that digitally signs contracts. We want to trick Bob into signing a fraudulent contract, without knowing, so that we can later suggest that he approved it. What we need to find are two contracts, one legitimate and one fraudulent, which produce the same hash value when passed through f(x).
假设鲍勃是通过数字方式签署合同的机构。 我们想欺骗鲍勃在不知情的情况下签署欺诈性合同,以便我们以后可以建议他批准该合同。 我们需要找到两个合同,一个合法合同,一个欺诈合同,当通过f(x)传递时会产生相同的哈希值。
For each contract, we can identify many ways of subtly changing it, without altering its meaning. For example, you could add differing amounts of white-space at the end of each line, slightly alter the pixels in a logo, or make small changes to the formatting. In combination this gives us millions of technically different but semantically identical documents, which in Bob’s eyes would all get the stamp of approval. It also gives us millions of variations on the fraudulent document. If we find a pair of documents, one legitimate, one fraudulent, that produce the same hash, then we can pass the legitimate one to Bob for signing, and then use that signature to “prove” the authenticity of the fraudulent contract.
对于每个合同,我们可以找到许多在不改变其含义的情况下对其进行细微更改的方法。 例如,您可以在每行的末尾添加不同数量的空格,略微更改徽标中的像素,或对格式进行小的更改。 结合起来,我们得到了数以百万计的技术上不同但语义相同的文档,在Bob看来,这些文档都将获得认可。 它还为我们提供了数以百万计的欺诈性文件变体。 如果我们找到一对产生相同散列的合法的,一个欺诈的文件,那么我们可以将合法的文件传递给Bob进行签名,然后使用该签名来“证明”欺诈性合同的真实性。
Thanks to the Birthday Paradox, the likelihood of at least one hash value collision between one of the legitimate and one of the fraudulent documents is much higher than might be expected, given the huge range of the hash function. In fact, the number of documents you need to produce is around the square root of the number of possible outputs of the hash function. This is improved by the fact that no hash function is perfectly uniformly distributed, which has led to many popular hashing algorithms becoming insecure.
多亏了生日悖论,鉴于散列函数的范围很广,合法文档之一与欺诈文档之一之间至少发生一次哈希值冲突的可能性比预期的要高得多。 实际上,您需要生成的文档数量大约是散列函数可能输出的数量的平方根。 没有散列函数可以完美地均匀分布这一事实得到了改善,这导致许多流行的散列算法变得不安全 。
翻译自: https://towardsdatascience.com/the-birthday-paradox-ec71357d45f3
python生日悖论分析
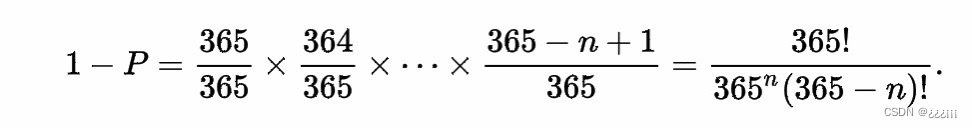











![[HTML+CSS+Vue.js] 超长文本等内容默认折叠显示,点击展开全文,再点击收起(仿知乎效果)](https://img-blog.csdnimg.cn/20181116052303524.gif)