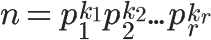OneAlert 入门(一)——事件流
OneAlert 是国内首个 SaaS 模式的云告警平台,集成国内外主流监控/支撑系统,实现一个平台上集中处理所有 IT 事件,提升 IT 可靠性。它能以史上第二快的速度,对事件进行智能的组织、排序和分类,从而极大地提高团队在处理运维告警与事件时的协作能力。本文是 OneAlert 入门系列文章的第一篇,主要介绍事件流。

事件流
OneAlert 界面最重要的部分便是事件流。只需点击菜单中部的告警图标,就能追踪并管理所有的告警,不论它们来自什么监控工具 —— Zabbix ,Nagios ,Solarwinds, AWS CloudWatch,Open-Falcon,阿里云 ,监控宝,腾讯云等十几种都能支持,而且新的应用正在快速集成。
自动智能归类告警
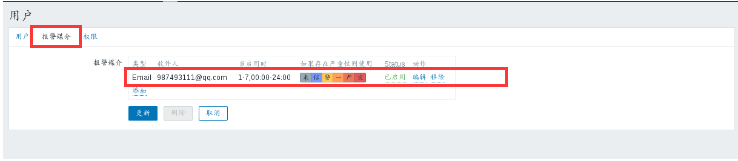
现有的多数软件缺陷追踪系统、工单管理系统以及问题追踪工具都不是针对 IT、NOC 以及 DevOps 设计的,基本上每个工单都必须由用户手动创建。但是,这并不适用于当今的 DevOps。传统的告警往往是由于超出监控栈中阈值而自动生成的,这些告警数量庞大,少则上百条,多则上千条。OneAlert 能自动分析这些告警,将它们按照主机、集群或者应用智能地进行组合,形成事件。
实时监控
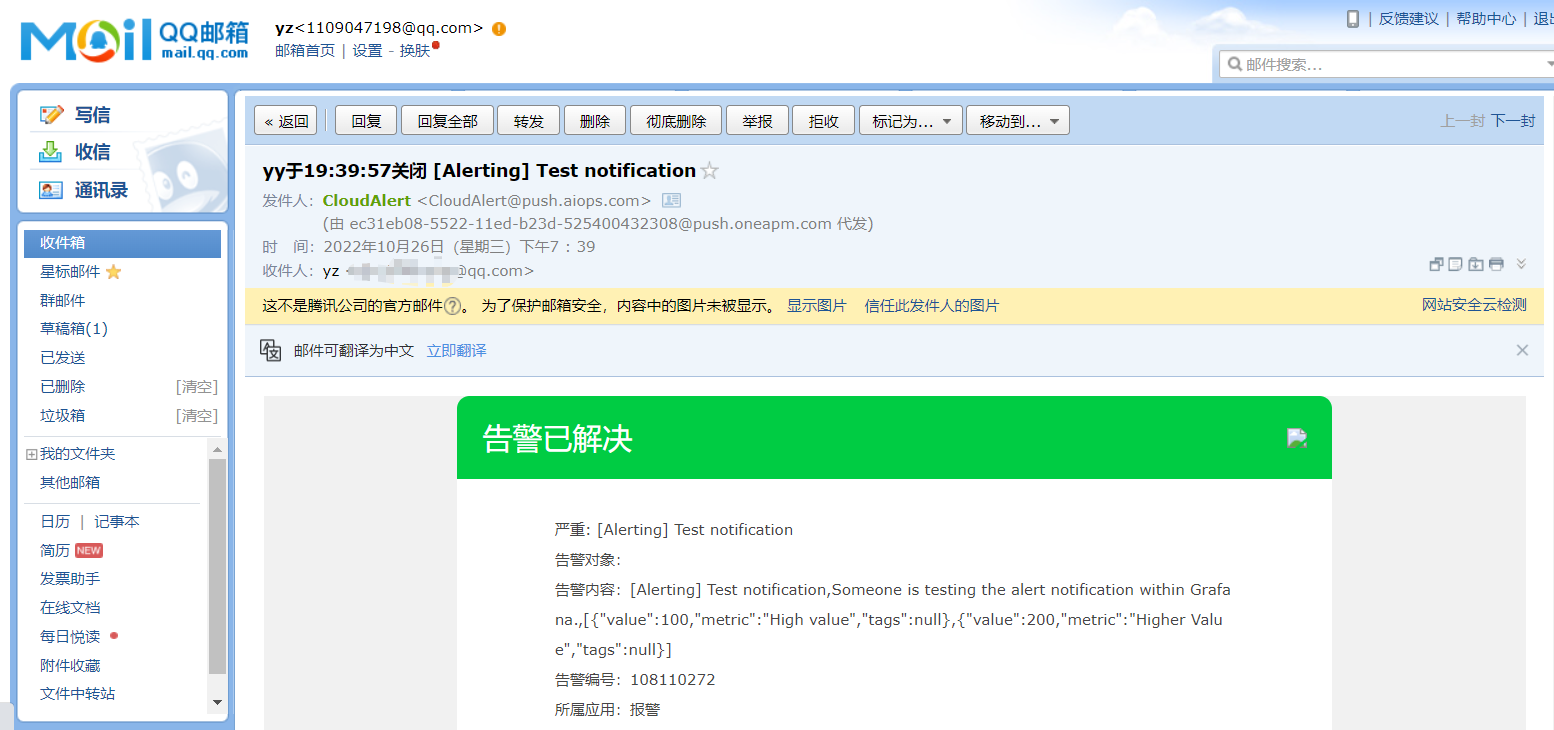
OneAlert 支持实时更新数据,确保 OneAlert 对事件不断整合、实时更新。每一个系统、应用的状态变化,不论其来自何种监控工具,都能即时传递到 OneAlert 的事件流中。
公司的成功取决于 IT 应用环境的可靠性。有了 OneAlert ,维护 IT 应用环境变得高效和便捷。既然你已经了解了 OneAlert 事件流的基本功能,下一步可以学习其日常的实际应用,将会在第二部分讨论,事件排序与分类。
本文转自 OneAPM 官方博客





![[JavaScript实例] 兼容IE和最新FF的复制粘贴代码](http://pp.a.5d6d.com/userdirs/e/d/vku88/attachments/month_0906/090611114190dab43e9b14b4a6.jpg)