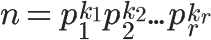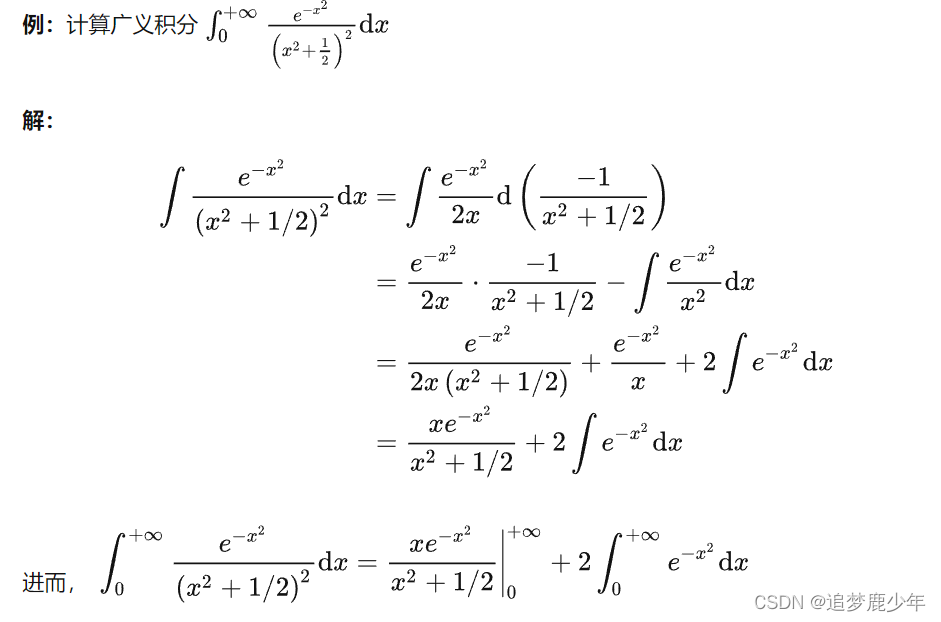一、注册云告警账号
1.登录云告警系统www.onealert.com，注册一个账号，注册过程不再这里介绍，点击CA进入平台

2.进入平台后，点击个人信息，绑定微信号，用于接收告警信息

3.点击配置---->通知策略，可以看到任何时间所有告警会以微信通知

4.获取应用key，点击配置—>应用---->添加应用—>zabbix

二、配置服务
1.解压告警软件到zabbix的监控告警目录下（必须在该路径下，否则会报错，告警不能及时送达）

[root@server1 ~]# tar zxf oneitsm_zabbix_release-1.2.0.tar.gz -C /usr/lib/zabbix/alertscripts/

2.切换到/usr/lib/zabbix/alertscripts/目录下，查看有解压软件
[root@server1 ~]# cd /usr/lib/zabbix/alertscripts/
[root@server1 alertscripts]# ls
oneitsm

3.进入/oneitsm/bin/下，利用应用key安装

[root@server1 alertscripts]# cd oneitsm/
[root@server1 oneitsm]# ls
bin  logs  release  update
[root@server1 oneitsm]# cd bin/
[root@server1 bin]# ./install.sh 79cb5db4-1693-3c88-1b97-ae483a68a437          ##这一长串数，就是刚刚在云告警平台添加的应用key
start to create config file...
Zabbix管理地址: http://172.25.21.1/zabbix
Zabbix管理员账号: Admin

三、在zabbix的web界面中添加告警媒介
1.点击管理—>报警媒介类型，将其他的报警媒介类型都禁用掉，只留oneitsm
2.查看告警用户，会自动添加oneitsm
3.触发器触动告警条件
4.查看操作，出现问题时的报警操作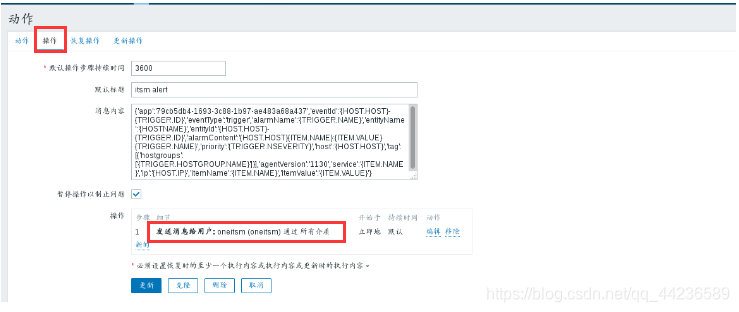

• 测试告警

1.关闭server2的zabbix-agent服务

[root@server2 ~]# systemctl stop zabbix-agent

2.等待5分钟左右，会触发告警

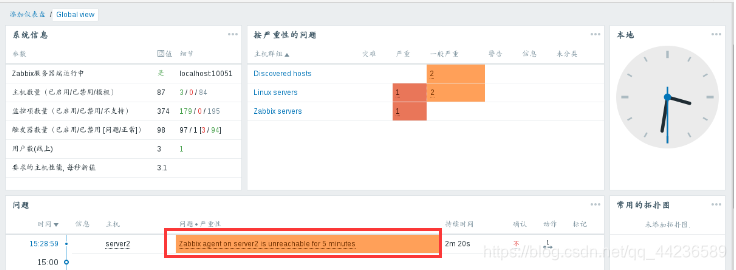
3.此时微信会接收到告警信息，进入云告警平台点击我的告警，待处理显示数量一，点击认领

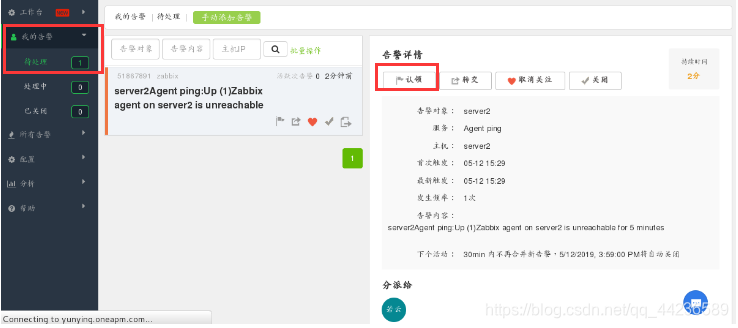
4.点击认领后，云告警页面的待处理任务就会变成处理中，可以看到操作日志，谁认领了，告警给谁等信息

5.在手动开启server2的zabbix-agent服务

[root@server2 ~]# systemctl start zabbix-agent

6.过一会zabbix监控界面的报警信息会自己消失，云告警平台会显示已经关闭告警

• 如何通过邮件的形式接收告警
  1.首先确保server1可以上网

[root@server1 ~]# ping www.baidu.com

2.安装mailx

[root@server1 ~]# yum install -y mailx

3.测试给自己发邮件看是否可以接收成功

[root@server1 ~]# mail root
Subject: test
hahaah
haja
.
EOT
[root@server1 ~]# mailq
Mail queue is empty
You have new mail in /var/spool/mail/root
[root@server1 ~]# mail
Heirloom Mail version 12.5 7/5/10.  Type ? for help.
"/var/spool/mail/root": 3 messages 3 new
>N  1 root                  Sun May 12 15:37  18/592   "haha"N  2 root                  Sun May 12 15:55  18/583   "root"N  3 root                  Sun May 12 15:56  19/590   "test"
& 3
Message  3:
From root@server1.localdomain  Sun May 12 15:56:37 2019
Return-Path: <root@server1.localdomain>
X-Original-To: root
Delivered-To: root@server1.localdomain
Date: Sun, 12 May 2019 15:56:37 +0800
To: root@server1.localdomain
Subject: test
User-Agent: Heirloom mailx 12.5 7/5/10
Content-Type: text/plain; charset=us-ascii
From: root@server1.localdomain (root)
Status: Rhahaah        ##可以看到刚才发送的邮件内容，代表邮件可以正常发送
haja& q
Held 3 messages in /var/spool/mail/root
You have mail in /var/spool/mail/root

4.在垃圾中点击反垃圾，设置邮件地址白名单

5.禁用刚才的云告警

6.点击管理—>报警媒介类型，将其他的报警媒介类型都禁用掉，只启用Email


7.进入用户，点击Admin，添加告警用户



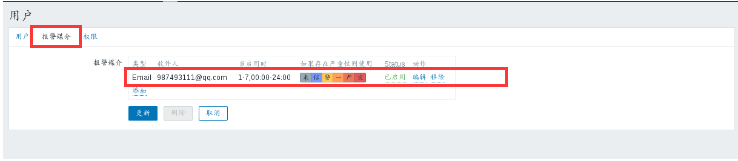
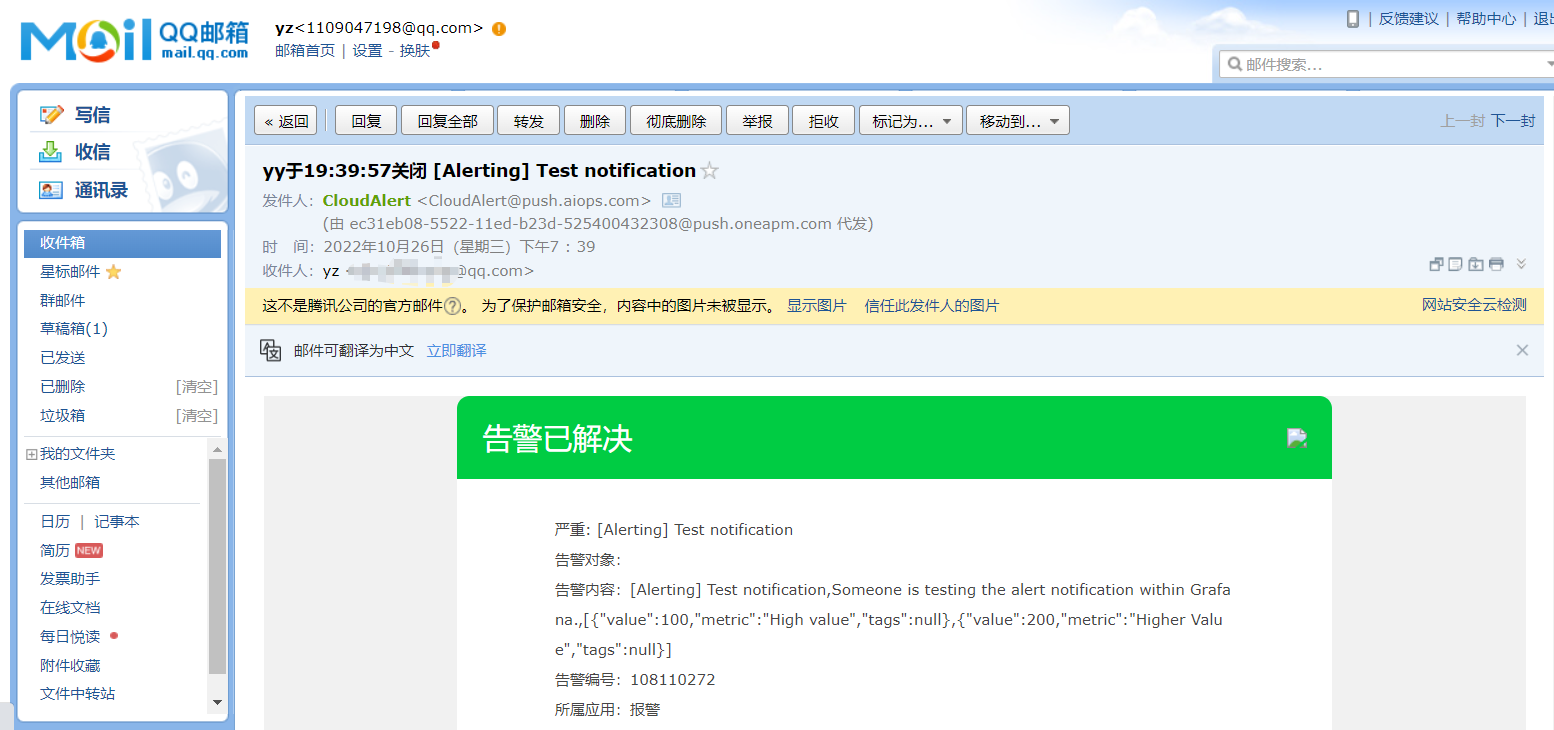
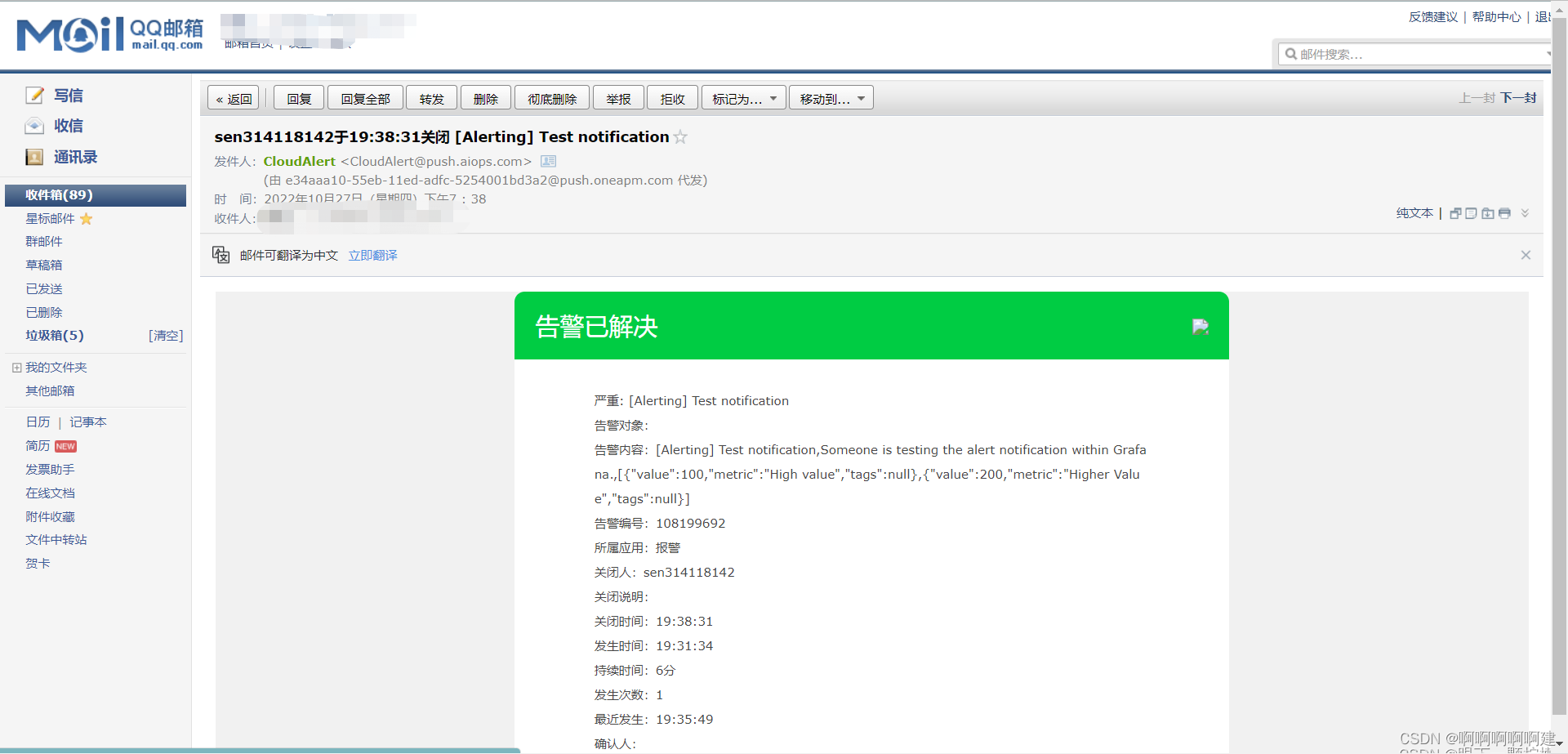
8.测试：手动关掉agent端，过5分钟左右，邮箱会出现告警信息

[root@server3 ~]# systemctl stop zabbix-agent