欧拉函数

1. 定义

什么是欧拉函数？

任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系？（比如，在1到8之中，有多少个数与8构成互质关系？）

计算这个值的方法就叫做欧拉函数，用φ(n)表示。在1到8之中，与8形成互质关系的是1、3、5、7，所以 φ(n) = 4。

2. 计算

欧拉函数计算公式

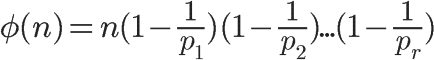
这个p是什么呢？

一个正整数 n 可以通过分解质因数得到

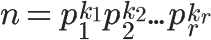
例如n = 100我们就可以写成 100 = 2^2 * 5^2，所以，2和5分别是p1和p2，因此欧拉值 φ(100) = 100 * (1- 1/2) * (1 - 1/5)

那么知道了这个公式与原理，我们怎么编程去计算呢？

关键的几步

1. 找到这个数的所有因子
2. 将把(1- 1/p)转换为(p - 1) / p
3. 筛去相同的因子

int euler(int n) {int ans = n;for (int i = 2; i*i <= ans; i++) {if (n % i == 0) {   ans = ans / i * (i-1);// 将相同的因子除去while (n % i == 0) {n /= i;}}}if (n > 1) {ans = ans / n * (n-1);}return ans;
}

由于本文主要目的是讲如何计算，欧拉函数公式的推导过程可以参考维基百科：欧拉函数