目录

前言

一、定义

1.告警功能概述

2.通知告警信息

3.prometheus监控系统的告警逻辑

1.告警功能:

2.静默、抑制、分组等功能;

二、Grafana+onealert报警

登陆http://www.onealert.com/→注册帐户→登入后台管理​编辑

​编辑 获取appkey

 1.在Grafana中配置Webhook URL

 2.测试cpu负载告警

 3.测试报警

 开始测试

 睿象云中也提示告警信息

我们解决问题后，只需在睿象云中将告警关闭就行，就会当作问题被解决了

​编辑 邮件中会告知告警已解决

---

前言

Prometheus对指标的收集、存储同告警能力分属于Prometheus Server和AlertManager(通用的组件)两个独立的组件，前者仅负责基于"告警规则"生成告警通知，具体的告警操作则由后者完成;

Alertmanager负责处理由客户端发来的告警通知客户端通常是Prometheus server，但它也支持接收来自其它工具的告警;
Alertmanager对告警通知进行分组、去重后，根据路由规则将其路由到不同的receiver，如Email、短信或PagerDuty等;
目前Alertmanager还不支持钉钉，那用户完全可以通过Webhook与钉钉机器人进行集成，从而通过钉钉接收告警信息。同时AltManager还提供了静默和告警抑制机制来对告警通知行为进行优化
PS:webhook是一个APr概念, webhoo是一种web回调或者http的push APT.Webhook作为一个轻量的事件处理应用
 

一、定义

1.告警功能概述

prometheus对指标的收集、存储与告警能力分属于Prometheus serve和alertmanager两个独立的组件，pro-server只负责通过"告警规则"生成告警通知，具体告警操作是由alertmmanager完成
告警规则：
是由PromQL编写的布尔值表达式使用>< =与一个常用量值，比如80%进行比较，其返回值为true或false

prometheus-server对抓取到的指标序列与告警规则中做为比较的Prometheus匹配，则会把此样本值抓取过来作比较，若返回值为true则认为指标异常，不能满足false，则为正常值以上表达式为告警规则表达式
比如：筛选一个指标数据cpu使用率<0%系统异常
 

2.通知告警信息

一旦条件表达式为true了就会触发通知信息，送给altermanager，由alter借助特定服务的API或者访问入口，将此信息发出去一般称为告警媒介，也可以借助邮件进行告警SMTP

3.prometheus监控系统的告警逻辑

route：告警路由，分组、分类分发告警消息给不同渠道

prometheus通过alter-rule规则，生成告警通知给altermanager
altermanager会生成本地的告警路由表（第一路由默认称为根路由，所有的告警信息都需要一个根路由，没有一个匹配项，则需要设置一个默认路由）为实现将特定的信息发送给特定的用户
例如：
按消息级别来看，严重、中等、普通级别，红色报警、蓝色报警，应用发送方
按分组：业务运维、系统运维、基础设施运维、k8s运维

1.告警功能:

除了基本的告警通知能力外，Altermanager还支持对告警进行去重、分组、抑制、

2.静默、抑制、分组等功能;

分组 （Grouping):将相似告警合并为单个告警通知的机制，在系统因大面积故障而触发告警潮时，分组机制能避免用户被大量的告警噪声淹没，进而导致关键信息的隐没;
抑制(Inhibition):系统中某个组件或服务故障而触发告警通知后，那些依赖于该组件或服务的其它组件或服务可能也会因此而触发告警，抑制便是避免类似的级联告警的一种特性，从而让用户能将精力集中于真正的故障所在;
静默(silent):是指在一个特定的时间窗口内，即便接收到告警通知，Alertmanager也不会真正向用户发送告警信息的行为;通常，在系统例行维护期间，需要激活告警系统的静默特性;
路由(route):用于配置Alertmanager如何处理传入的特定类型的告警通知，其基本逻辑是根据路由匹配规则的匹配结果来确定处理当前告警通知的路径和行为
 

二、Grafana+onealert报警

Prometheus 报警需要使用 alertmanager 这个组件，而且报警规则需要手动编写（对运维来说不友好）。所以我这里选用 grafana+onealert 报警。注意：实现报警前把所有机器时间同步再检查一遍

登陆http://www.onealert.com/→注册帐户→登入后台管理

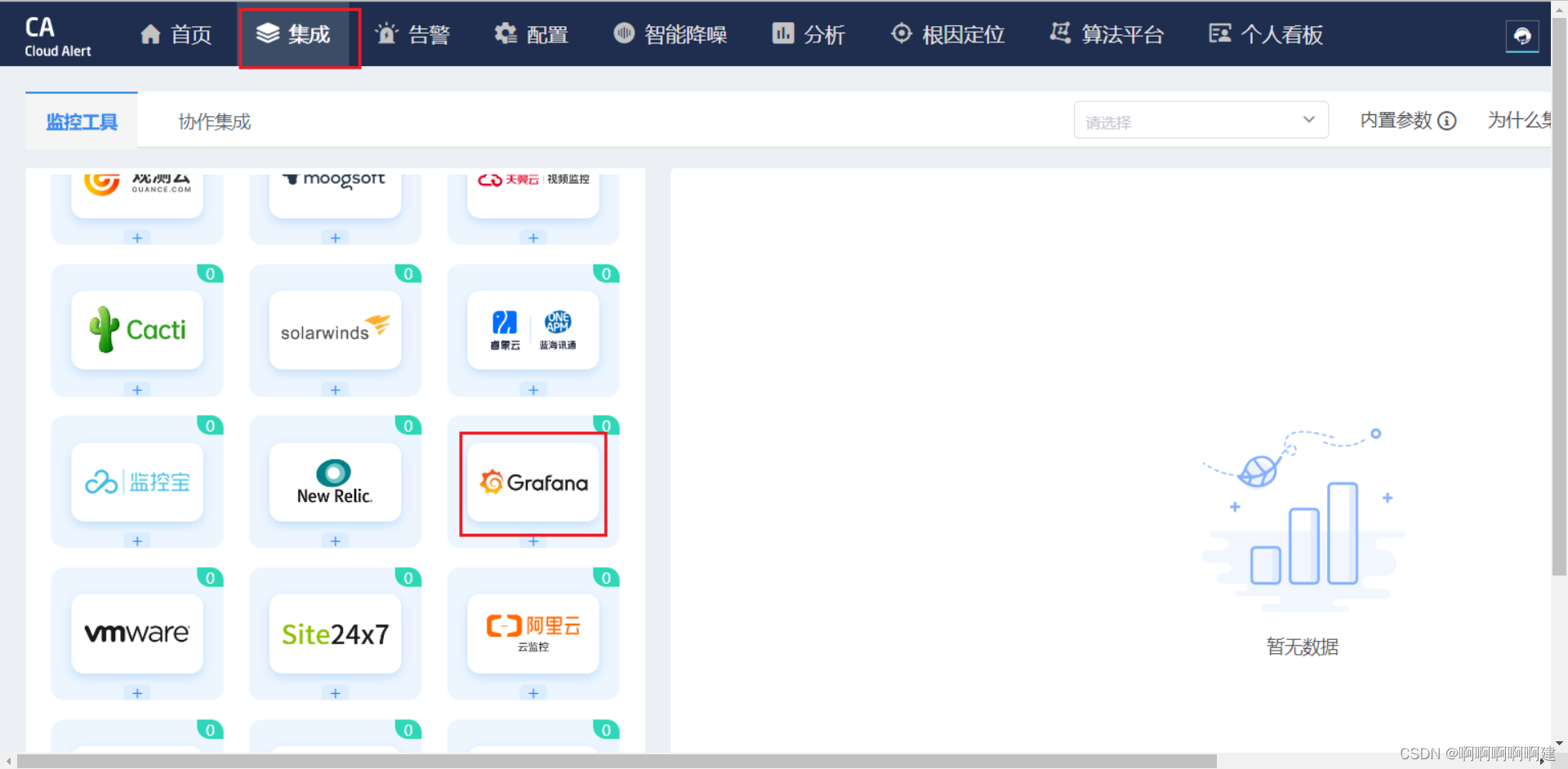
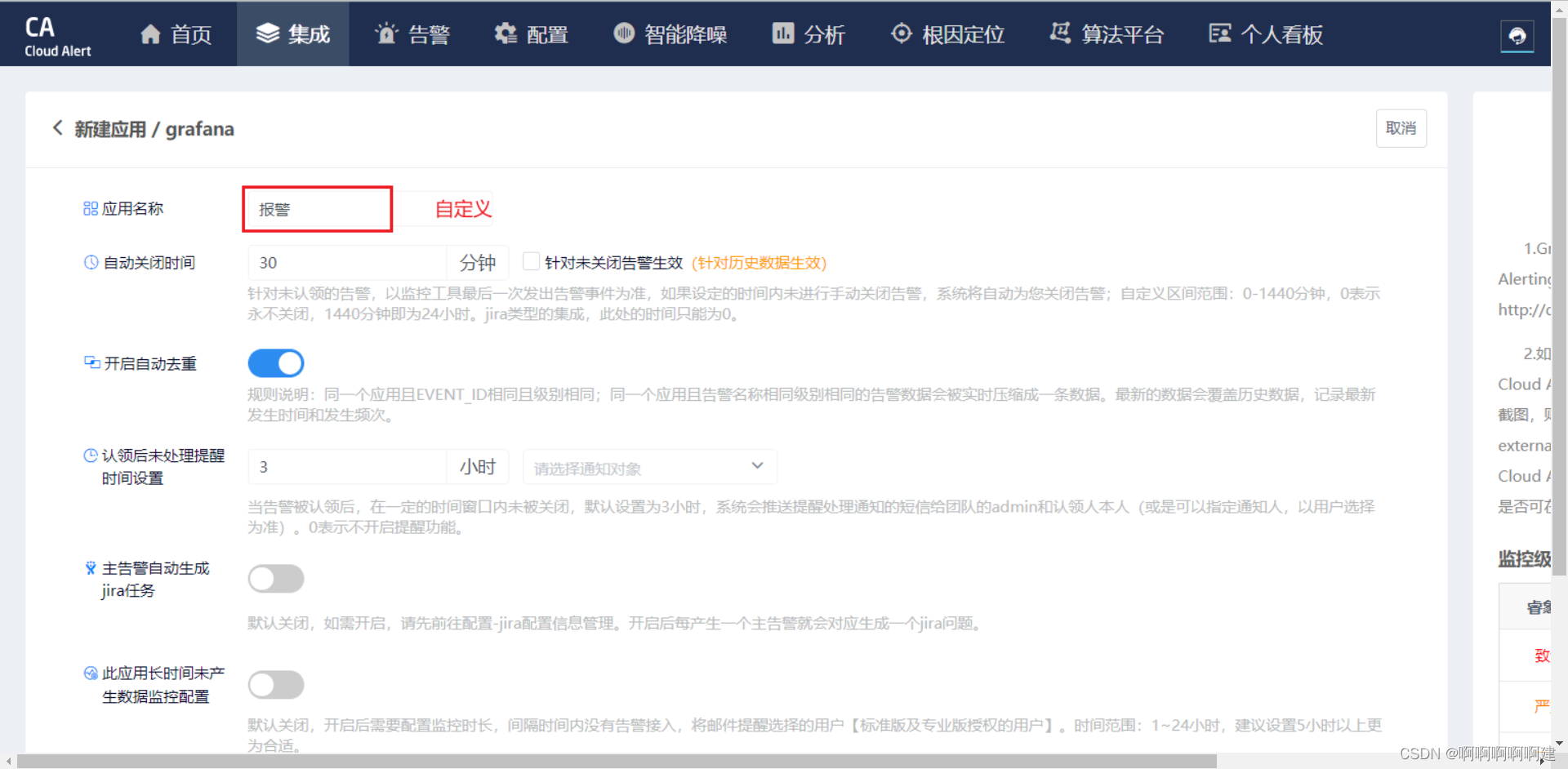 获取appkey

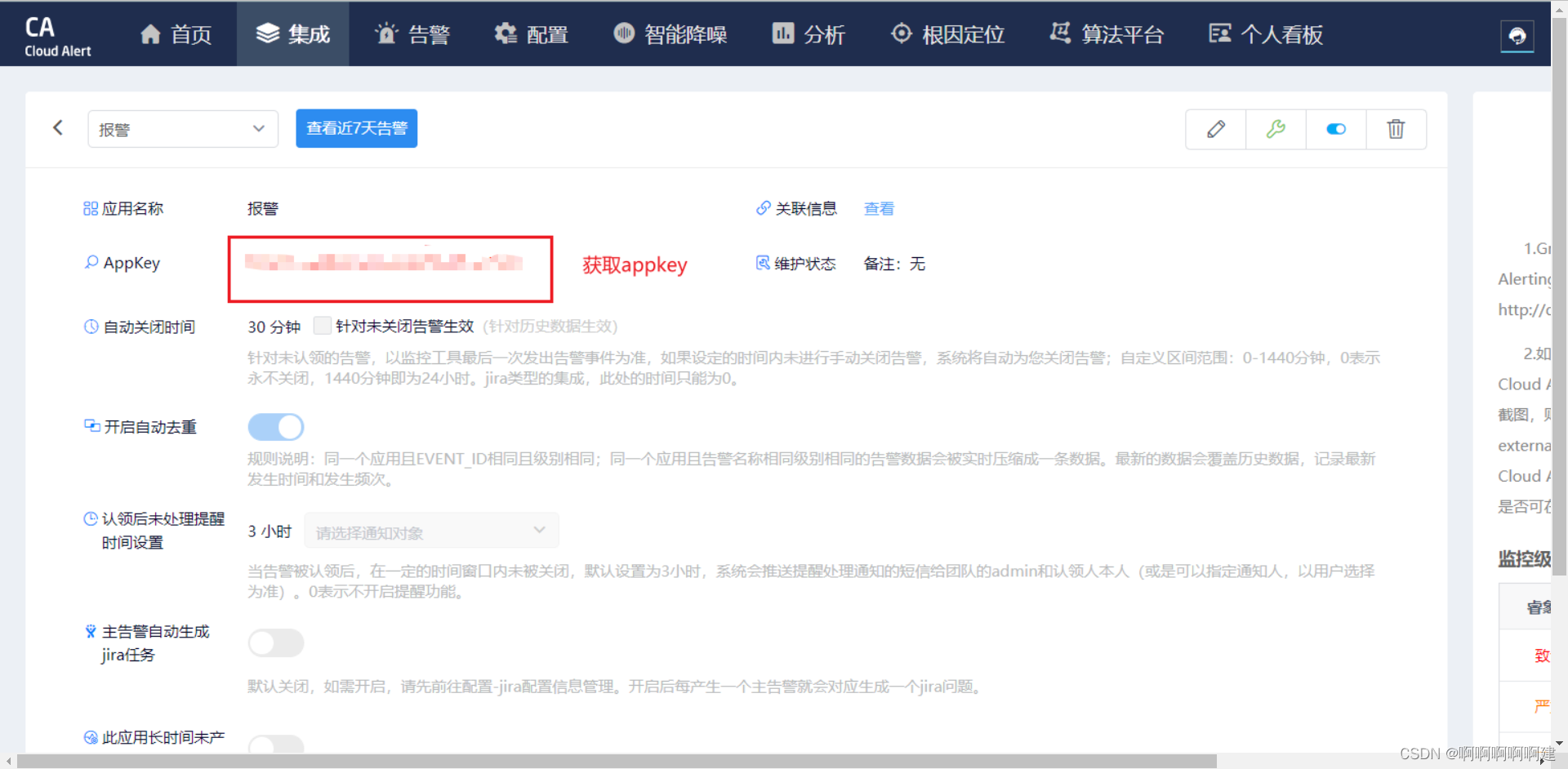
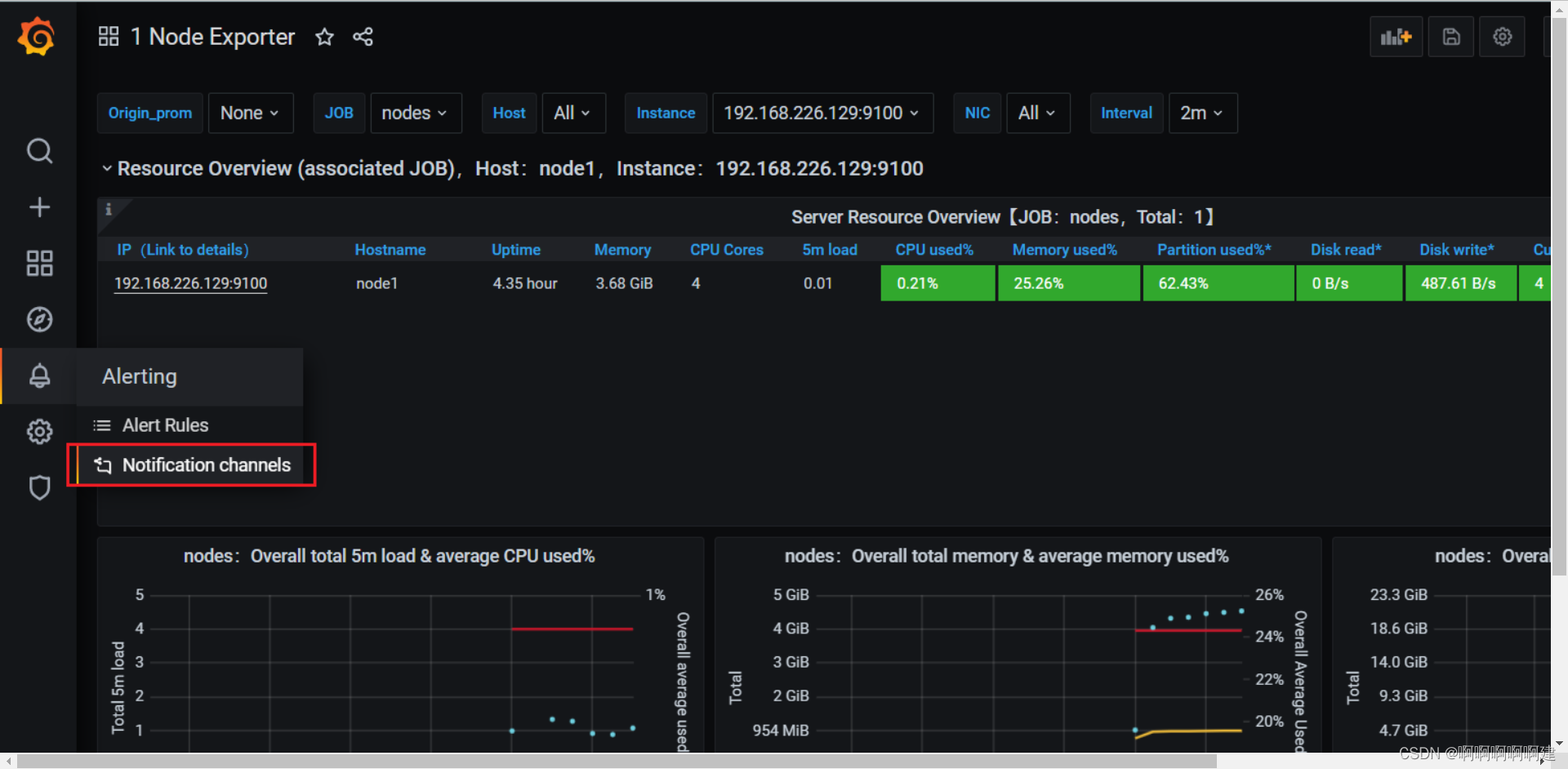
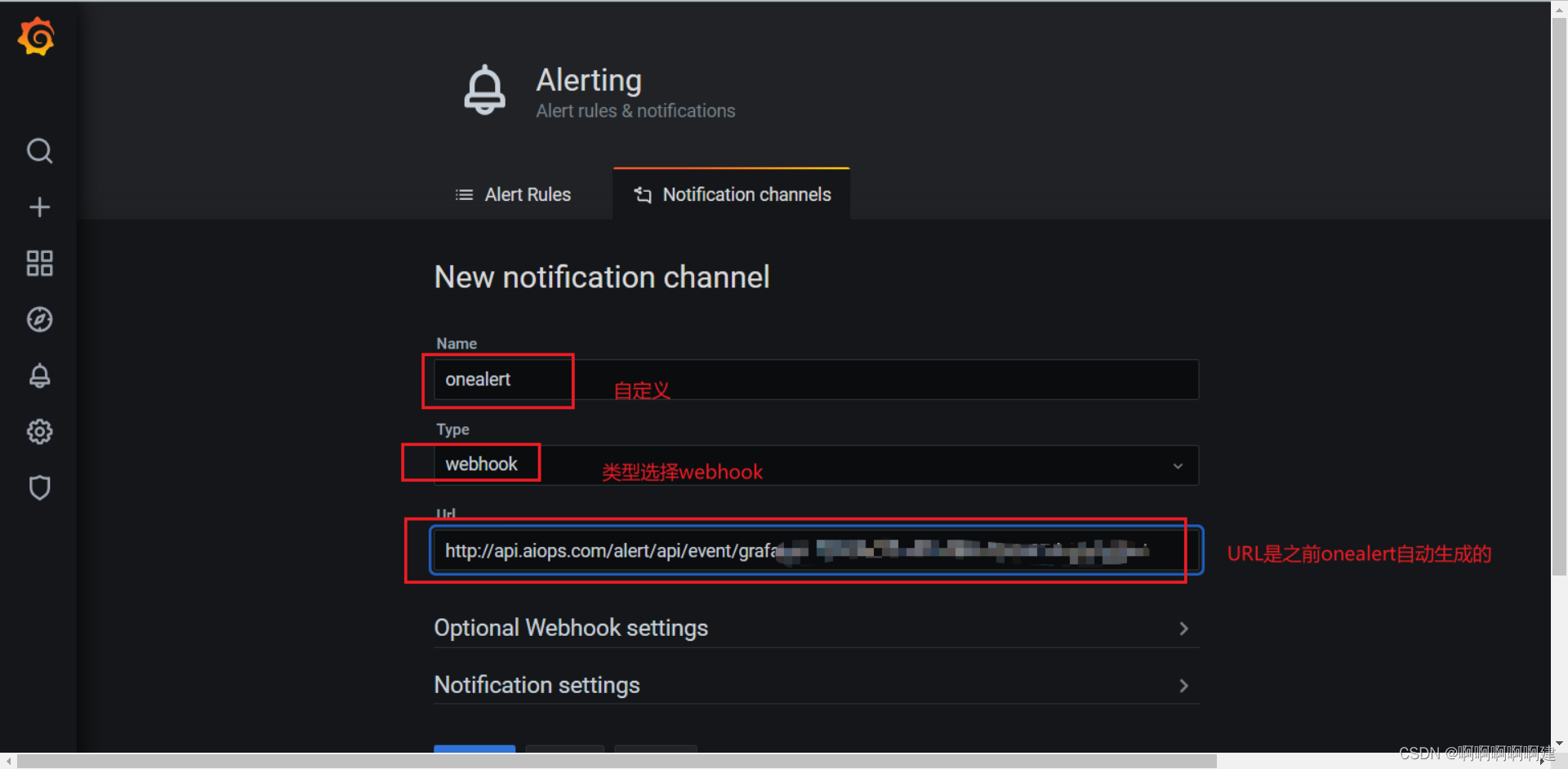
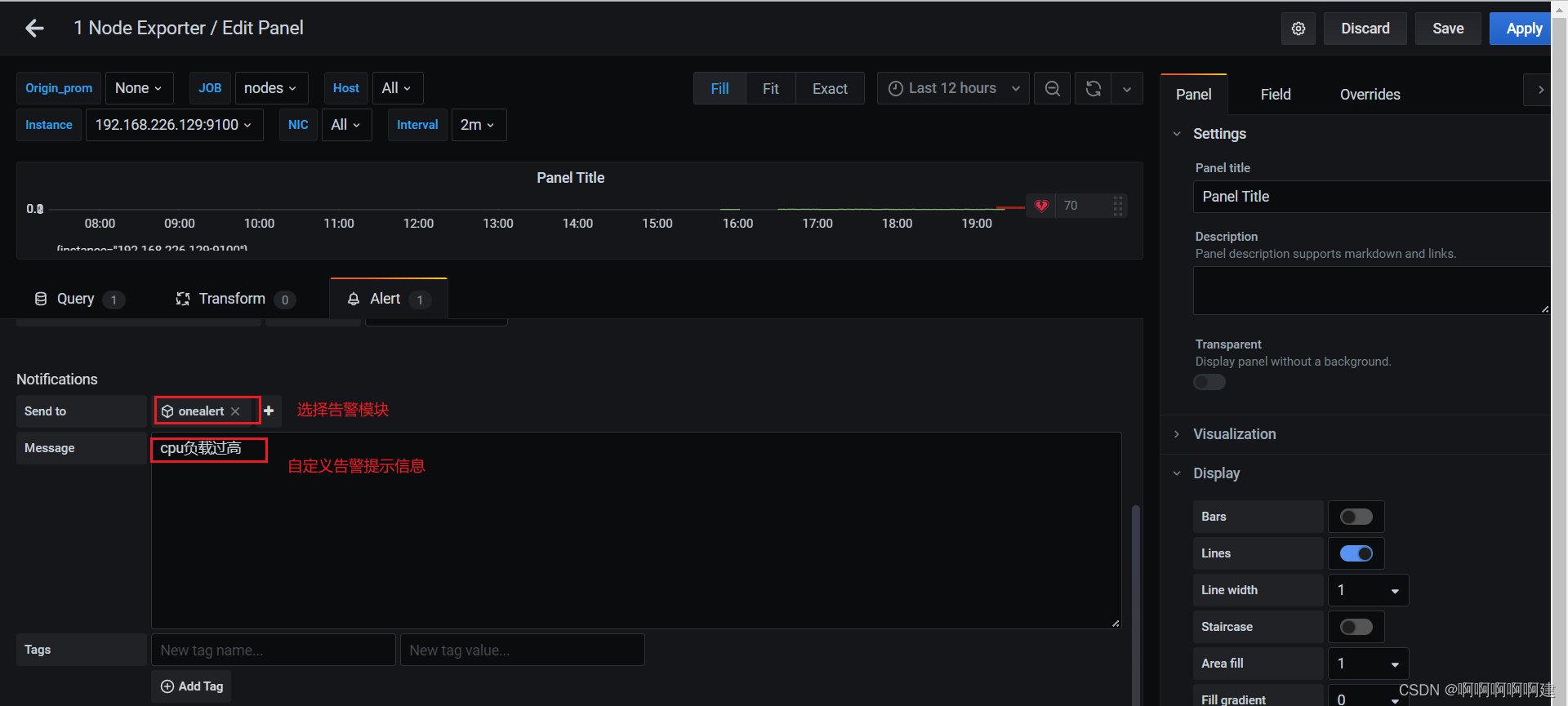
 1.在Grafana中配置Webhook URL

1、在Grafana中创建Notification channel，选择类型为Webhook；
2、推荐选中Send on all alerts和Include image，Cloud Alert体验更佳；
3、将第一步中生成的Webhook URL填入Webhook settings Url；
URL格式：
http://api.aiops.com/alert/api/event/prometheus/bd8cc0af7b2644f1834a8d0b9d9e5ced4、Http Method选择POST；
5、Send Test&Save；

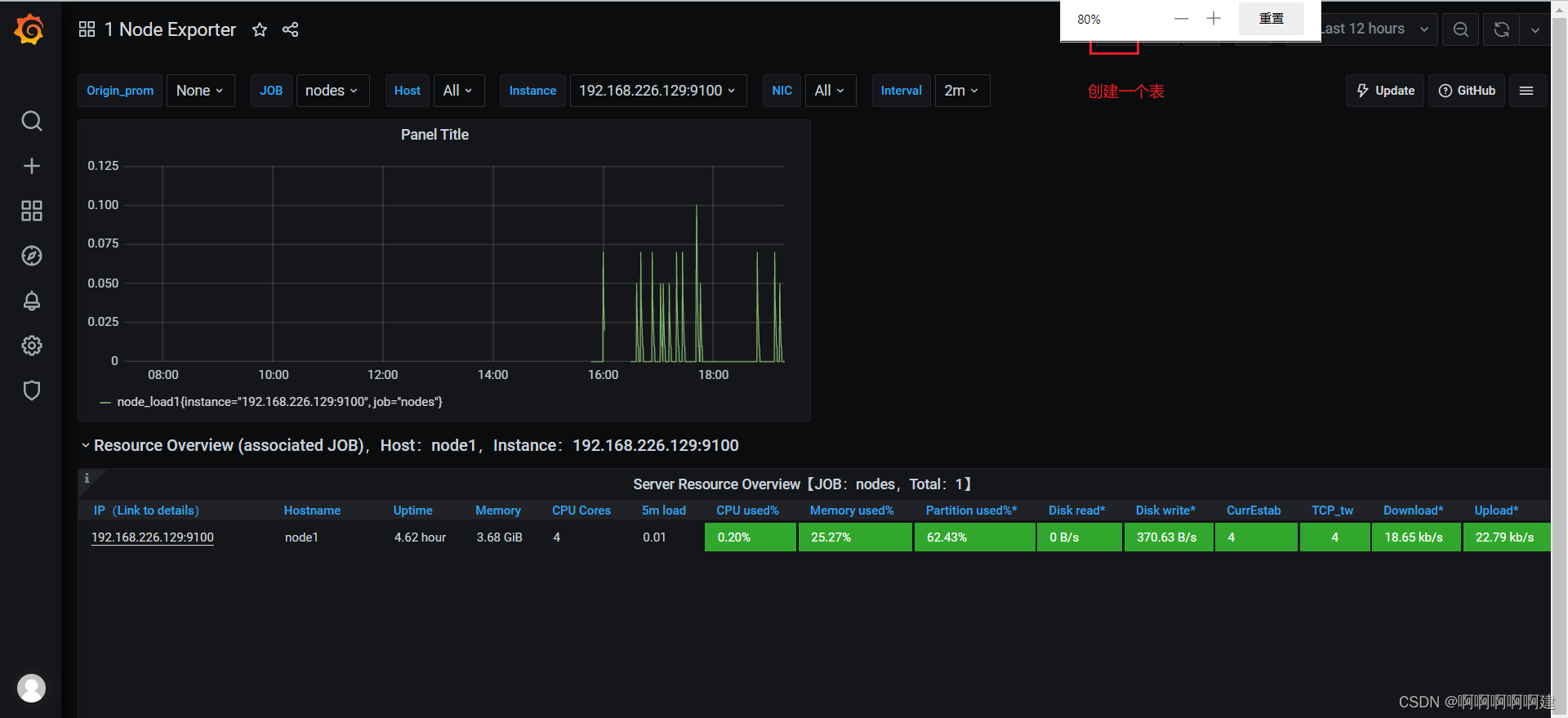
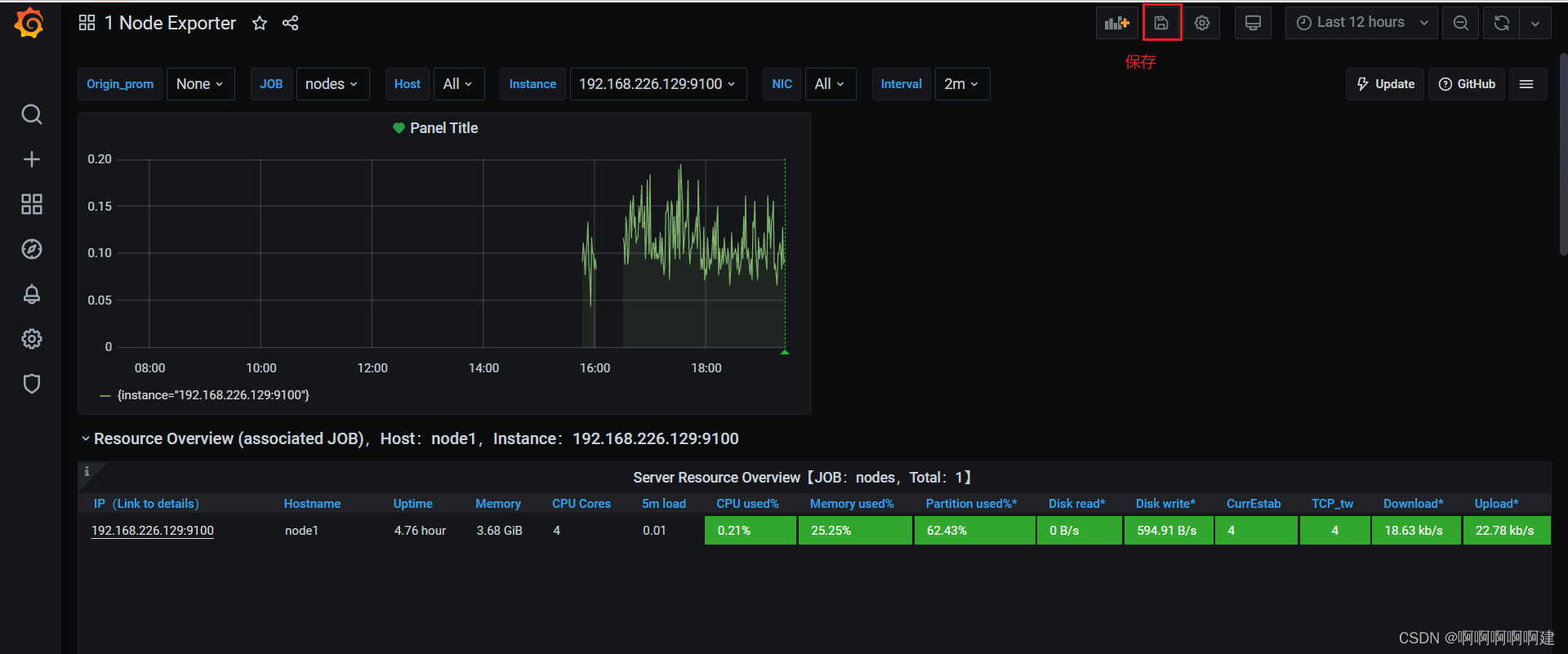
 2.测试cpu负载告警

现在可以去设置一个报警来测试了（这里以我们前面加的 cpu 负载监控来做测试）

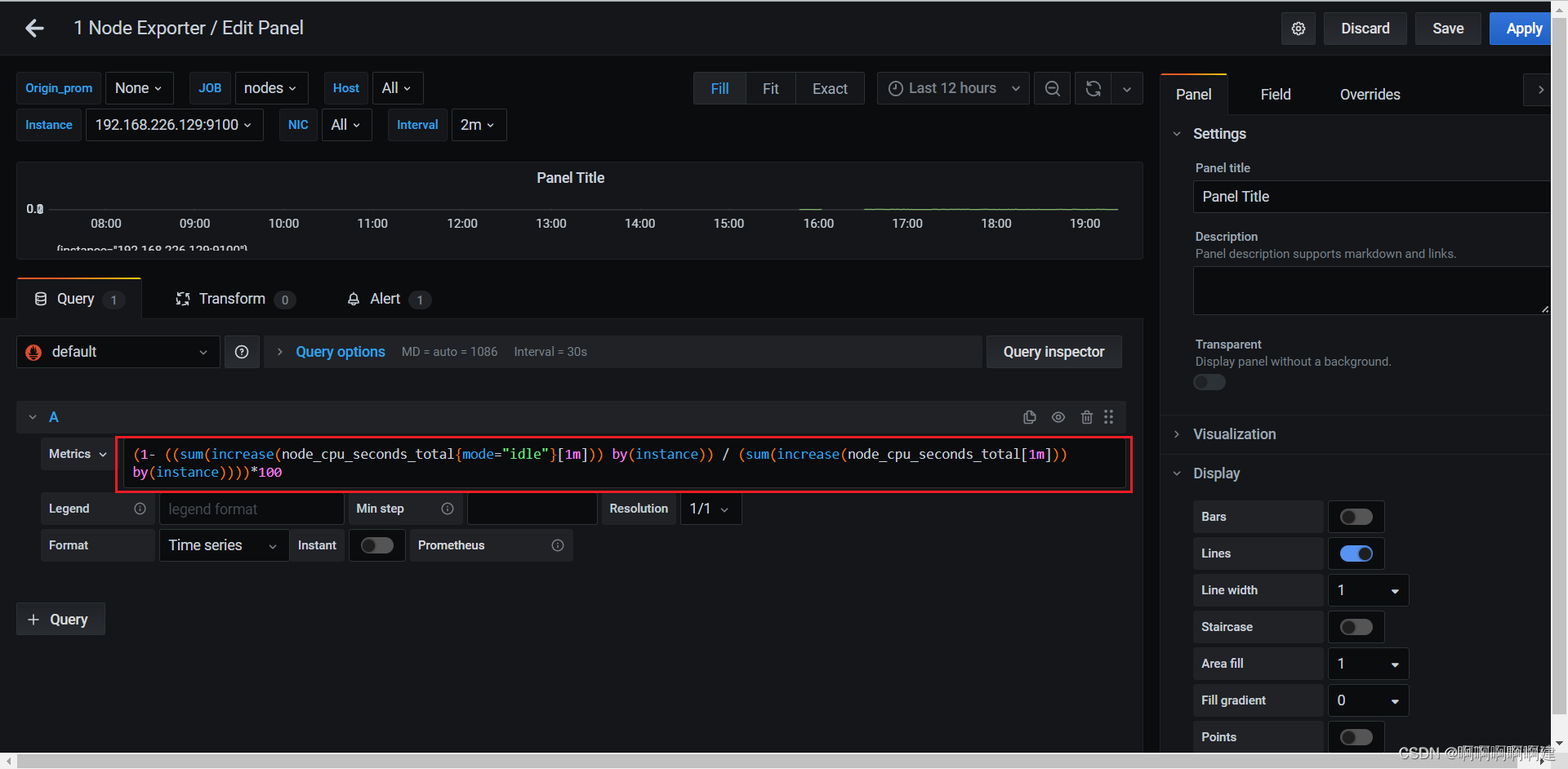
#查看cpu占用率
(1- ((sum(increase(node_cpu_seconds_total{mode="idle"}[1m])) by(instance)) / (sum(increase(node_cpu_seconds_total[1m])) by(instance))))*100

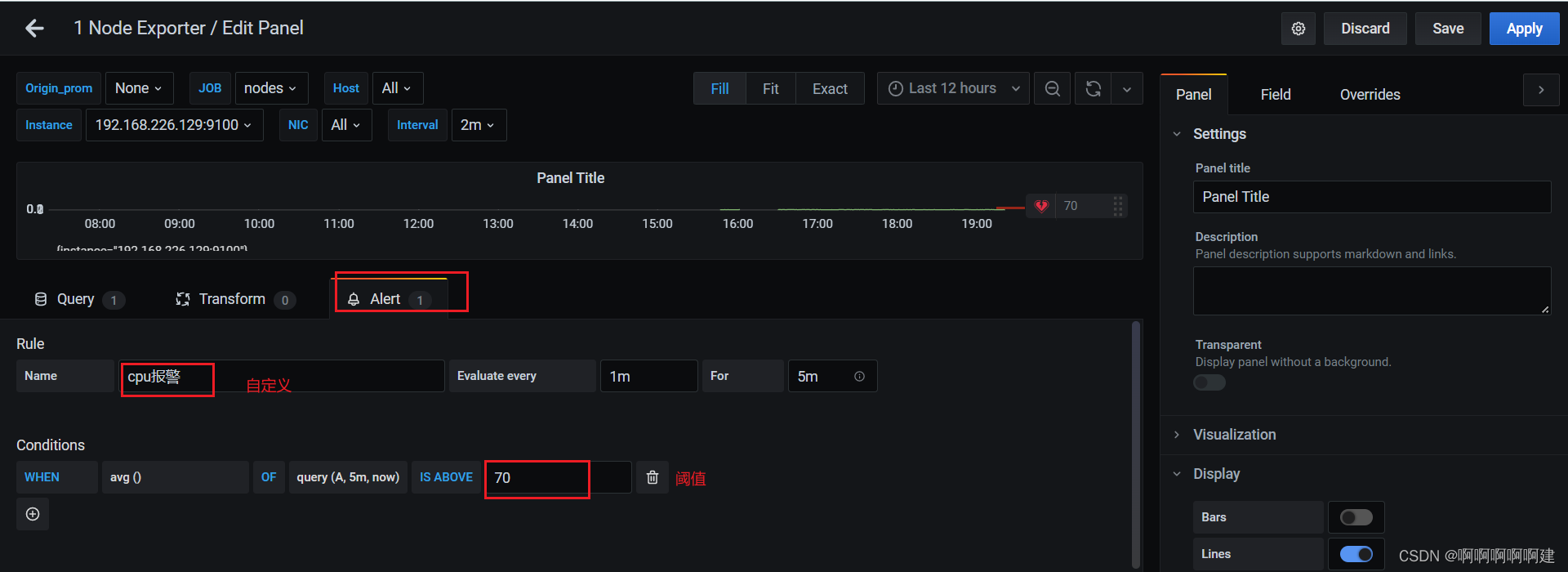
 3.测试报警

在被监控端下载一个stress测试工具

yum install -y epel*
yum install -y stress

 开始测试

设置4核cpu，此时cpu就会被冲高

发来的报警如下图

邮箱会发来报警邮件

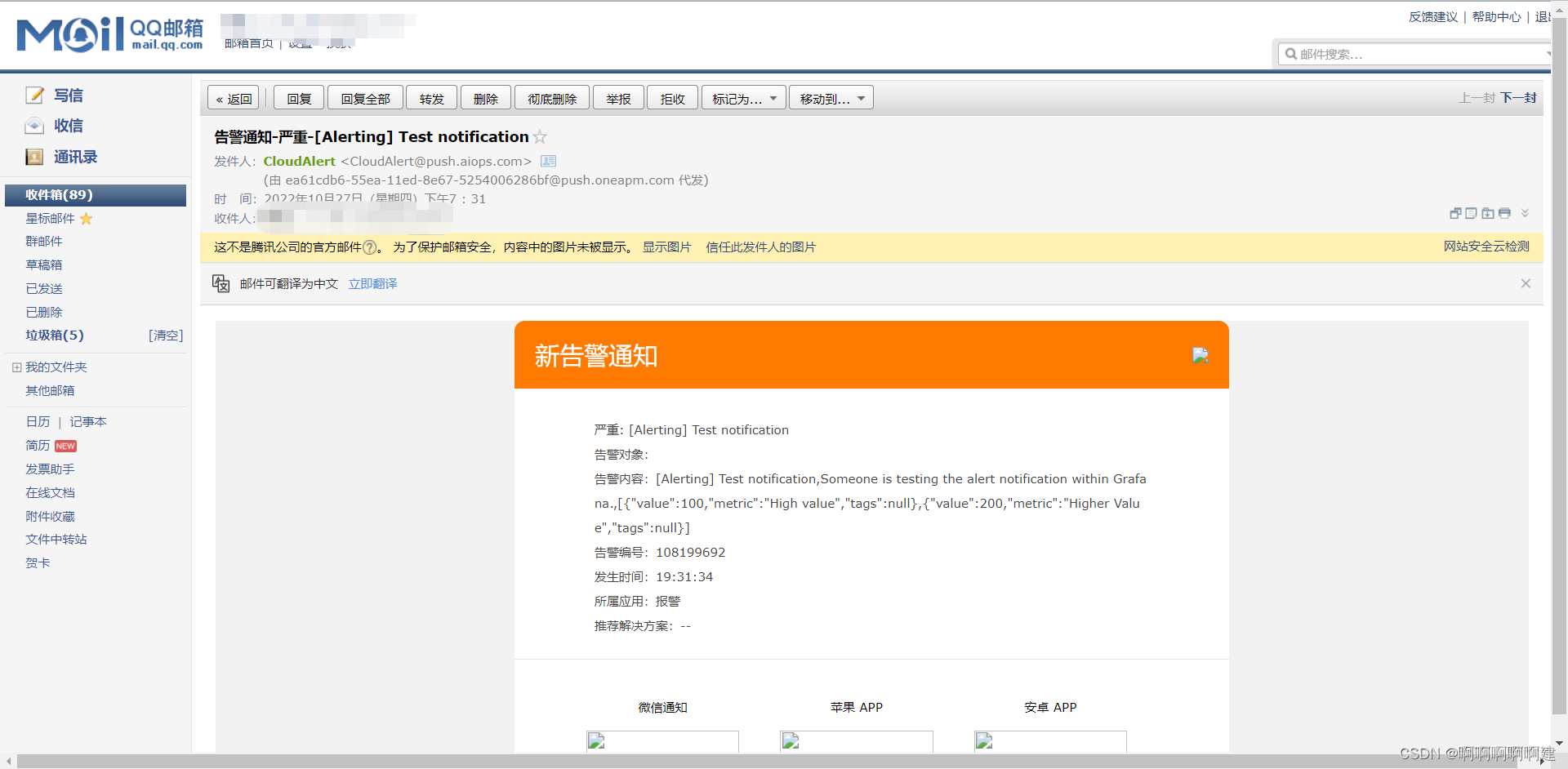
 睿象云中也提示告警信息

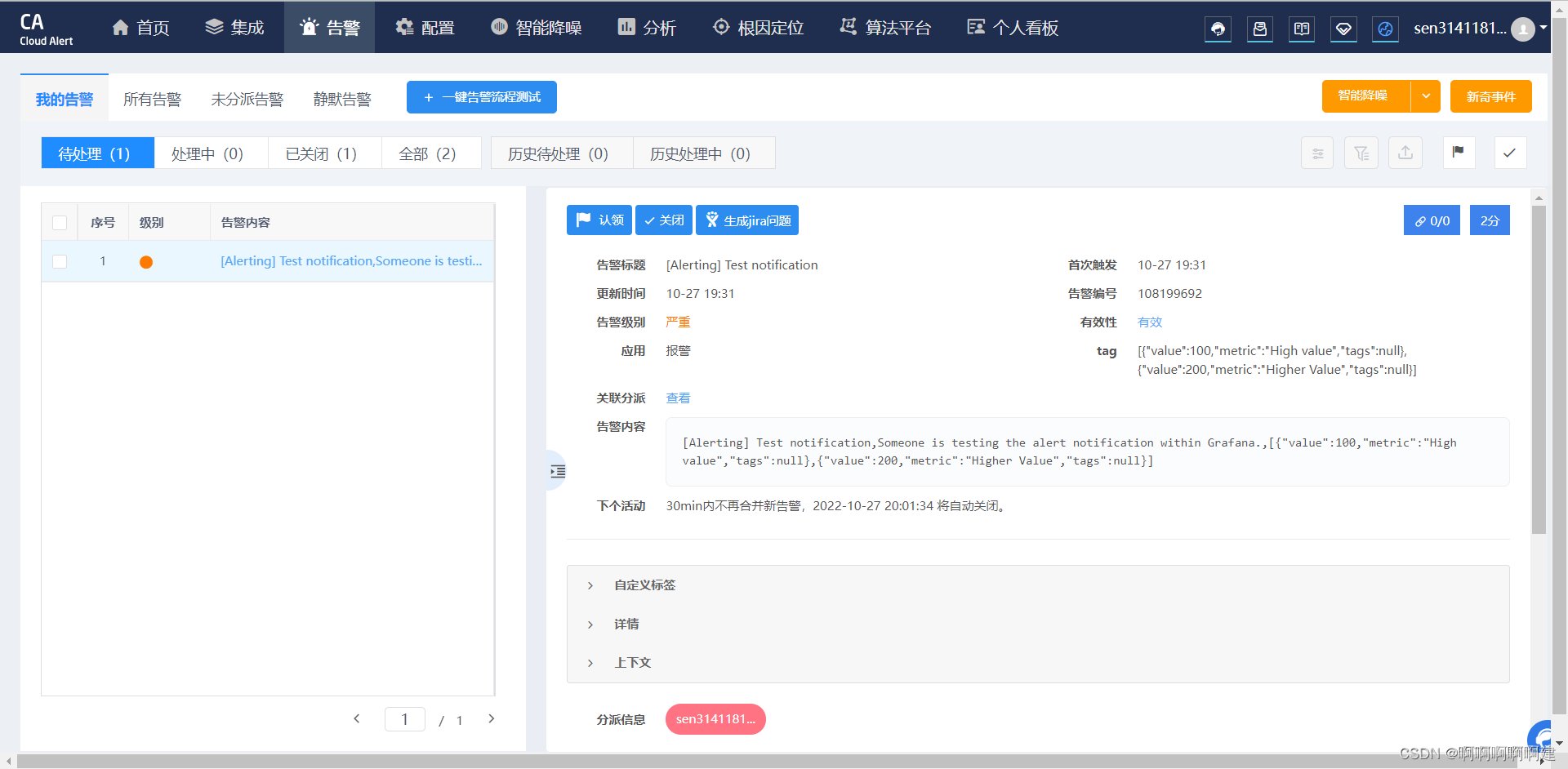
我们解决问题后，只需在睿象云中将告警关闭就行，就会当作问题被解决了

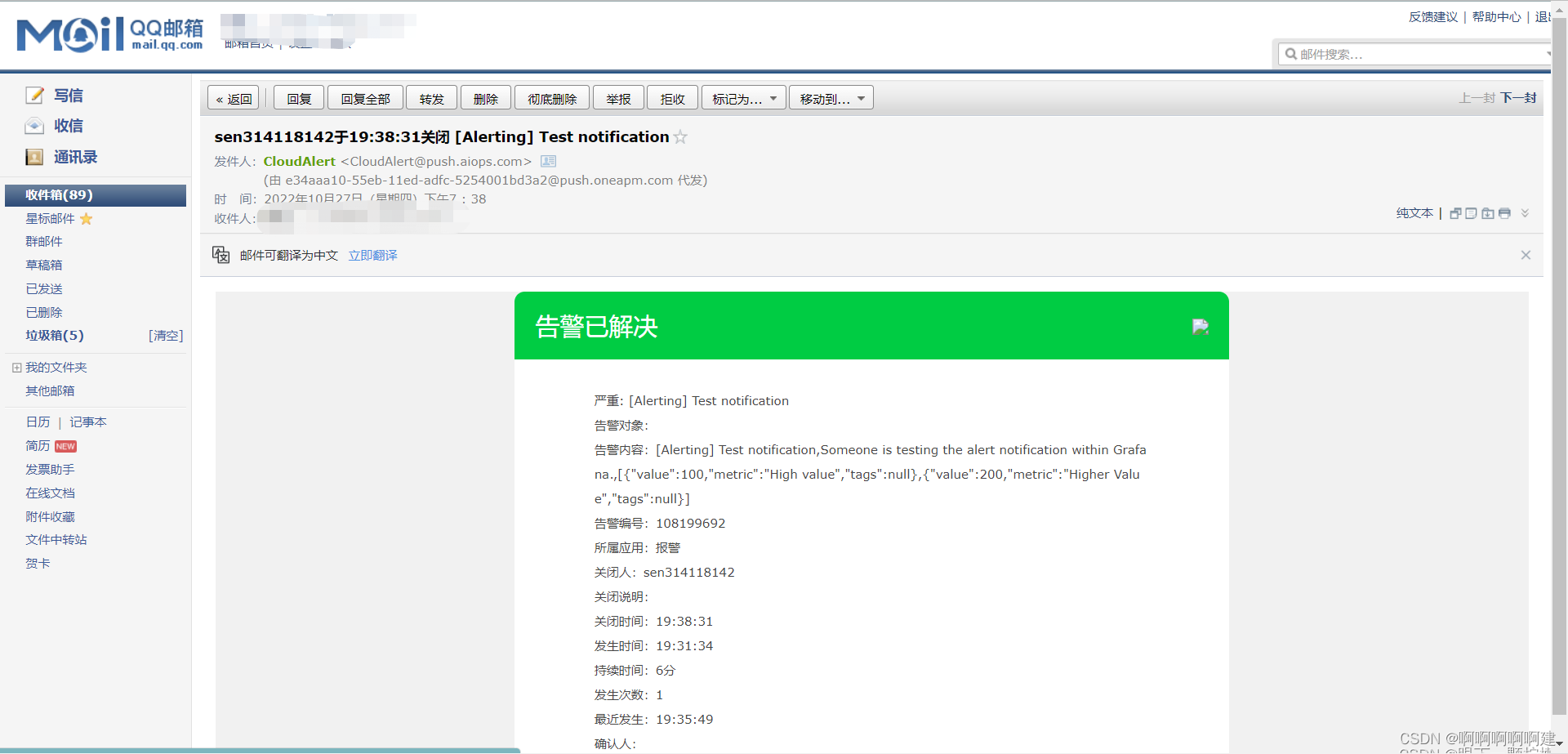
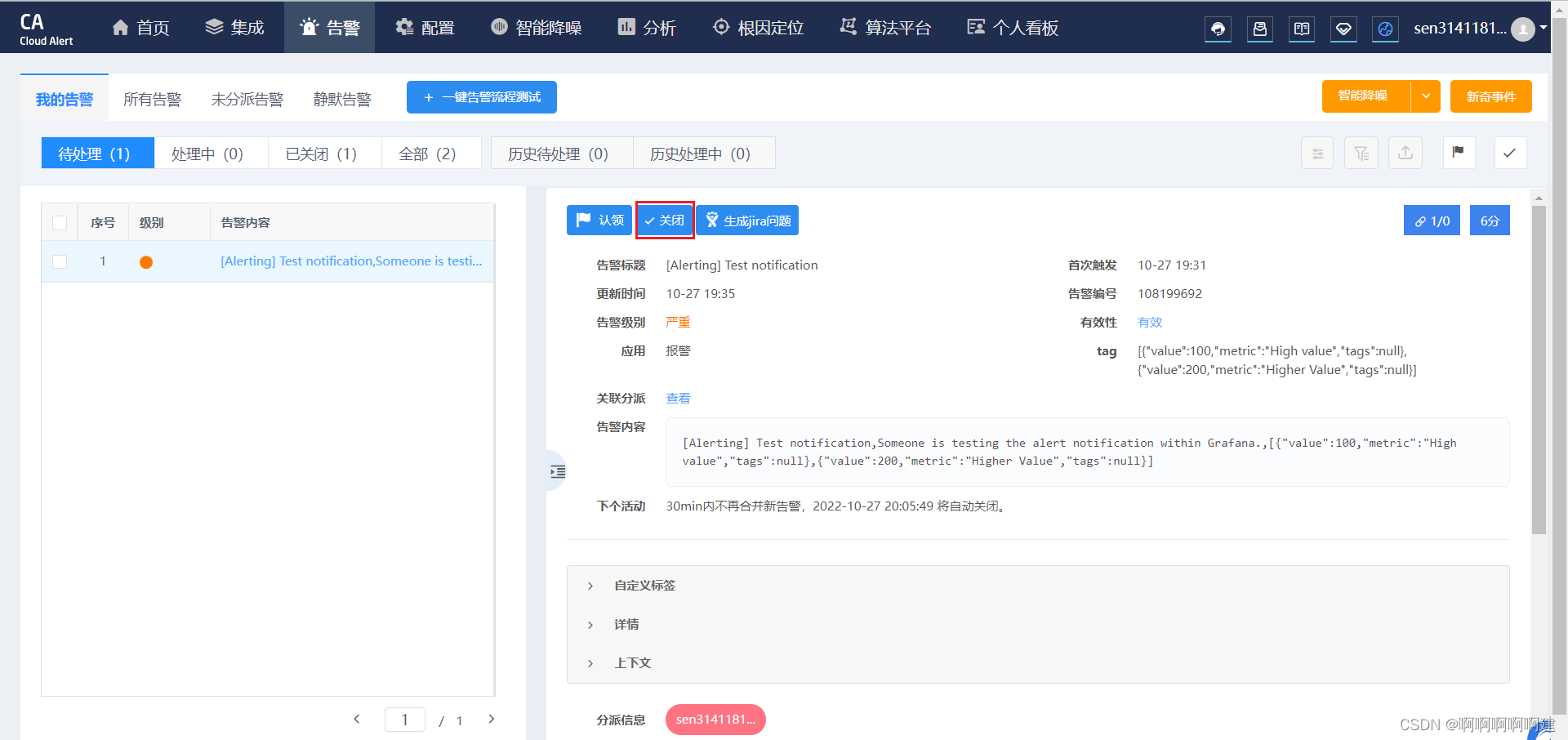 邮件中会告知告警已解决