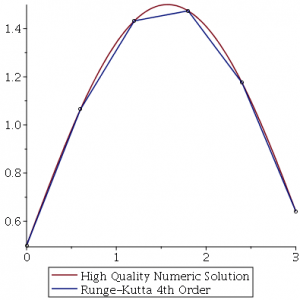
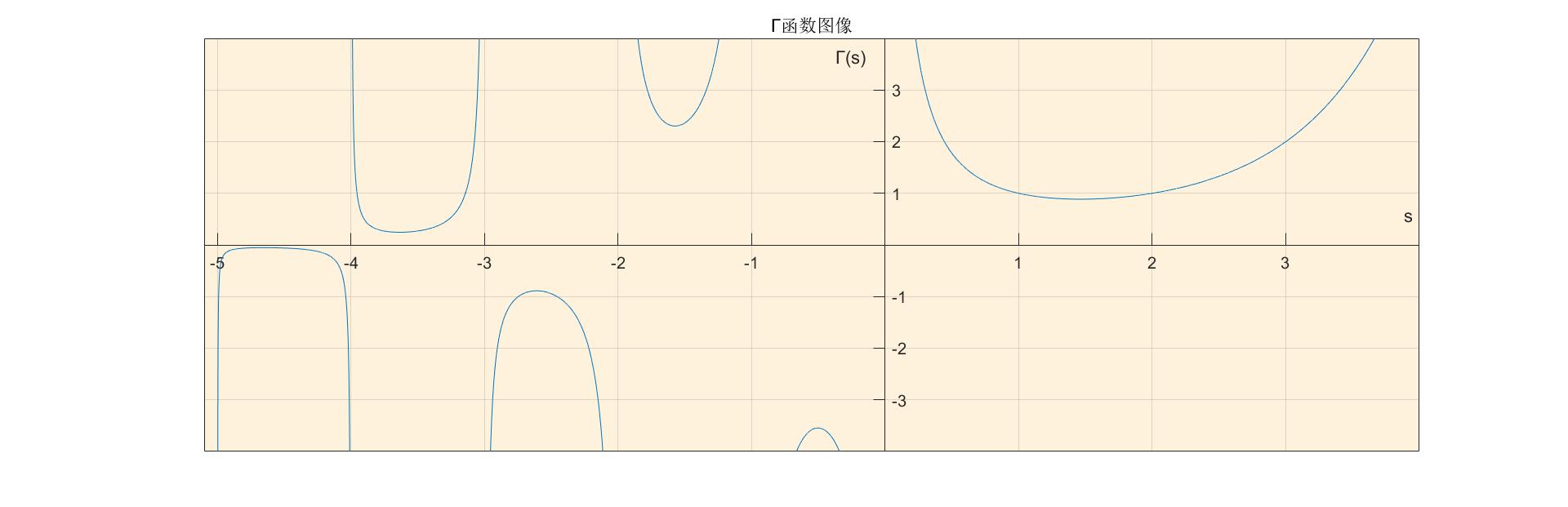
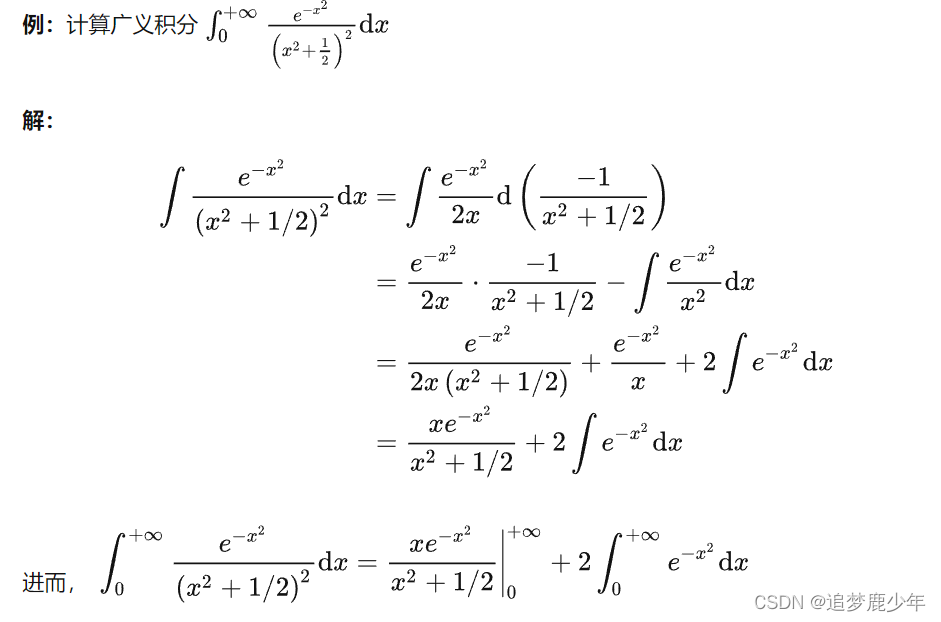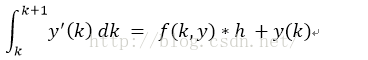ps:如果研究又遇到分数阶相关课题的童鞋可以与博主联系获取分数阶相关的源代码,不图什么,就图个点赞
一、问题简介
在最近的课题中接触到了分数阶导数相关的东西,比如函数 f ( t ) f(t) f(t)对t的0.5阶导等等,网上有一些对于分数阶导数的处理办法是将其放到频域中进行处理,根据大学《自动控制原理》等课程我们可以知道,通过拉氏变换我们可以将微积分运算变为代数运算,对一个输入信号进行一阶微分就是乘以s,一阶积分就是乘以 1 / s 1/s 1/s,因此对于0.5阶的微分运算可以看作 s 0.5 s^{0.5} s0.5,因此分数阶微积分运算可以看作是一个传递函数,通过整数阶的以 s s s为自变量的方程可以逼近s的分数阶方程,现在通过这种逼近模型得到了 s 0.5 s^{0.5} s0.5和 s 0.3 s^{0.3} s0.3两种运算的传递函数,利用Matlab观察到两种传递函数的bode图如下:


上述两幅图中的上半部分是传递函数的幅频特性曲线,下半部分是传递函数的相频特性曲线。在课程《自动控制原理》频率响应一章中我们可以知道将拉氏变换中的 s s s替换为 j w jw jw( j j j是虚数)之后得到一个新的与 w w w传递函数F(W),对于一个角频率为 w w w的输入正弦信号,系统会对这个正弦信号产生幅值和相位的变化,这就对应着F(W)的模值与相位,同样也可以得到幅频曲线和相频曲线。在分数阶导数中,以0.5阶导 s 0.5 s^{0.5} s0.5为例,将 s s s换成 j w jw jw得到 ( j w ) 0.5 = j 0.5 ∗ w 0.5 (jw)^{0.5}=j^{0.5}*w^{0.5} (jw)0.5=j0.5∗w0.5,此时出现了 j 0.5 j^{0.5} j0.5,这样分数阶导数的问题就变成了复数的分数阶次方的问题,但是出现虚数的0.5次方时应该如何求解其幅值和相角来验证由整数阶逼近模型得到的bode图是否正确呢?通过一系列的资料查阅后得到了两种解释虚数的分数阶次方 j a j^a ja(a为实数)的方法。
二、从虚数的定义说起
1、虚数的起源与定义
虚数i的定义其实十分简单,在我们的中学校园里就有学过,虚数i的平方等于-1,虚数就是-1的平方根。但是我们在学习过程中一直都不知道虚数究竟代表着什么,在虚数出现前的数学中有4中基本运算:+-×÷,假如对于一个实轴上的点,加减运算意味着点的向左向右的平移,而乘除可以看做是对轴线的拉伸与压缩(也可以看做是一种累积的连续作用),但是这些运算都没有解决旋转的表示,在虚数发明之前人们对于旋转的处理都显得十分麻烦,而虚数与复数的出现就使得旋转的处理大大简化。
前面说到 i 2 = − 1 i^2=-1 i2=−1,既可以写作 1 × i × i = − 1 1×i×i=-1 1×i×i=−1,乘法可以看做是一种连续的变化,那么可以想象,对于实轴上的点1经过了两次乘以i的变化变为了-1,相信大家已经知道了i代表着什么,没错,答案就是旋转,逆时针的旋转!如下图所示:

一个i就代表着逆时针旋转90°,而1经过两次乘以i的变换既逆时针旋转了180°,那么1就变成了-1。那么总结一下就是i代表了旋转,i是一个旋转量,i并不是一个数。
2、复数的引入
此时已经知道了i是一个旋转量,此时将实数作为横轴,虚数作为纵轴,并用加号将两种数连接起来就形成了复数 a + b i a+bi a+bi(也可以表示为 A ∠ a A∠a A∠a),复数拥有着和虚数很相似的性质。比如两个复数的相乘就等于其模值相乘,相角求和,其实就是模值相乘同时在第一个复数的相角基础上逆时针继续旋转相应的角度。
3.虚数的分数阶解释
在理解了虚数和复数的定义及意义后我们再来看 s 0 . 5 s^0.5 s0.5次方,将 s s s替换为 j w jw jw后得到 ( j w ) 0.5 = j 0.5 ∗ w 0.5 (jw)^{0.5}=j^{0.5} *w^{0.5} (jw)0.5=j0.5∗w0.5,由于j是一个虚数,是一个旋转量,因此 j 0.5 j^{0.5} j0.5的模值为1,因此 j w jw jw…的模值就等于 w 0.5 w^{0.5} w0.5。又由于乘以j表示旋转了90°,又 j = j 0.5 × j 0.5 j=j^{0.5}×j^{0.5} j=j0.5×j0.5,既经过连续的两次 j 0.5 j^{0.5} j0.5的变换后会逆时针旋转90°,既 j 0.5 j^{0.5} j0.5代表了旋转45°。因此我们可以得出结果, s 0.5 s^{0.5} s0.5的相角为恒定的45°,与上图中的44.8°基本一致,其幅值增益为 w 0.5 w^{0.5} w0.5,将增益写作对数形式则表示为 10 l o g w 10logw 10logw,因此如图一,当 w = 100 w=100 w=100是增益为20,与计算结果一致,最终判断逼近模型是正确的。
三、通过欧拉公式的计算来解释
欧拉公式也是我们在大学就学过的一个公式了,但我们对欧拉公式的了解也仅仅局限于公式之上,在下一次的公众号文章中我将会和大家讨论关于欧拉公式的起源与意义。在接下来的推导中我们以 s a s^a sa(a为实数)为例,将s替换为iw后得到 ( i w ) a = i a ∗ w a (iw)^a=i^a*w^a (iw)a=ia∗wa(这里的j用i来表示),此时通过欧拉公式来导出 i a i^a ia。
首先我们知道欧拉公式的表达式为 e i x = cos x + i ∗ sin x e^{i x}=\cos x+i * \sin x eix=cosx+i∗sinxi表示虚数,此时取 x = π / 2 x=π/2 x=π/2,则 c o s x = 0 cosx=0 cosx=0, s i n x = 1 sinx=1 sinx=1,因此得到公式: e π i 2 = i e^{\frac{\pi i}{2}}=i e2πi=i此时 i a i^a ia可以替换为 e π a i / 2 e^{πai/2} eπai/2,又将 e π a i / 2 e^{πai/2} eπai/2代入欧拉公式得到:
i a = e π a i 2 = cos π a 2 + i ∗ sin π a 2 = [ ( cos π a 2 ) 2 + ( ( sin π a 2 ) 2 ] ∠ π a 2 = ∠ π a 2 i^{a}=e^{\frac{\pi a i}{2}}=\cos \frac{\pi a}{2}+i * \sin \frac{\pi a}{2}=\left[\left(\cos \frac{\pi a}{2}\right)^{2}+\left(\left(\sin \frac{\pi a}{2}\right)^{2}\right] \angle \frac{\pi a}{2}=\angle \frac{\pi a}{2}\right. ia=e2πai=cos2πa+i∗sin2πa=[(cos2πa)2+((sin2πa)2]∠2πa=∠2πa
当a=0.3时, s 0.3 = w 0.3 ∗ i 0.3 = w 0.3 ∠ 27 ° s^{0.3}=w^{0.3}*i^{0.3}=w^{0.3}∠27° s0.3=w0.3∗i0.3=w0.3∠27°,相角恒定为27°与第二个bode图的相频曲线一致,而对于幅频特性,增益为 20 l o g ( w 0.3 ) = 6 l o g ( w ) 20log(w^{0.3})=6log(w) 20log(w0.3)=6log(w)此时取w=100,即增益为6*2=12,与逼近模型得到的幅频曲线一致,最终验证得到分数阶逼近模型正确。