积分方法讨论（数学表达与代码整理）

数学原理

1.1 四元数与角速度的关系

在无人机或无人车的导航系统中常常采用四元数代替欧拉角来表示机体的旋转，因为欧拉角在计算过程中容易产生奇异，这与欧拉角的计算需要利用正弦、余弦公式相关。

    机体姿态的计算中常常需要对四元数进行积分处理。博客¹中给出了四元数与机体角速度的关系，表示如下。下面的积分方法基于该公式。
$${\dot{q}}_e^b(t)=\frac{1}{2}\left[\begin{array}{cccc}0& -{\omega }_x& -{\omega }_y& -{\omega }_z\\ {\omega }_x& 0& {\omega }_z& -{\omega }_y\\ {\omega }_y& -{\omega }_z& 0& {\omega }_x\\ {\omega }_z& {\omega }_y& -{\omega }_x& 0\end{array}\right]q_e^b(t)$$

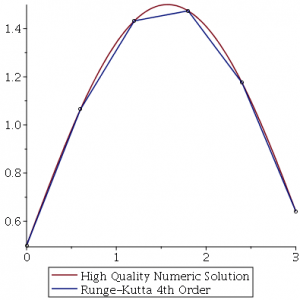
1.2 4阶龙格－库塔方法探讨（Runge-Kutta methods）²

算法如下：
$$\begin{array}{rl}& {\mathbf{q}}_{k+1}={\mathbf{q}}_k+\Delta t\frac{1}{6}\left({\mathbf{k}}_1+2{\mathbf{k}}_2+2{\mathbf{k}}_3+{\mathbf{k}}_4\right)\\ & \begin{array}{ll}{\mathbf{k}}_i=\mathbf{f}\left({\mathbf{q}}^{(i)},t_k+c_i\Delta t\right)& \\ {\mathbf{q}}^{(i)}={\mathbf{q}}_k,& \text{ for }i=1\\ {\mathbf{q}}^{(i)}={\mathbf{q}}_k+\Delta t{\sum }_{j=1}^{i-1}{a}_{ij}{\mathbf{k}}_j,& \text{ for }i>1\end{array}\end{array}$$
其中需要的系数$c_i$和$a_{i}j$是：
$$\begin{array}{rl}{c}_1=0,& c_2=\frac{1}{2},c_3=\frac{1}{2},c_4=1\\ a_{21}=\frac{1}{2},& a_{31}=0,a_{41}=0\\ a_{32}=\frac{1}{2},& a_{42}=0,a_{43}=1\end{array}$$
最后我们需要对四元数进行归一化处理。

1.3 欧拉积分³

1.4 中值积分

2 仿真部分

2.1 代码

1. 龙格－库塔

%% 
for k = 2:Nwp = imu_data(4:6, k-1);w1 = imu_data(4:6, k);w = (wp+w1)/2;ap = imu_data(1:3, k-1);a1 = imu_data(1:3, k);Ow = [0     -w(1)   -w(2)    -w(3);...w(1)   0       w(3)    -w(2);...w(2)  -w(3)    0        w(1);...w(3)   w(2)   -w(1)     0  ];Fc = 0.5*Ow;F = eye(4) + Fc*dt;%%或者在这里改变积分的方法(对于矩阵的积分方法)quat1 = attitude_update_RK4(quat,dt,wp,w1);%%R_S_n = quat2dcm(quat');R_S_n_1 = quat2dcm(quat1');acc_w = (R_S_n' * ap + gw   +   R_S_n_1' * a1 + gw)/2;%     quat = F* quat;quat = attitude_update_RK4(quat,dt,wp,w1);Pwb = Pwb + Vw * dt + 0.5 * dt * dt * acc_w;Vw = Vw + acc_w * dt;
%%quatAll(k,:) = quat';oula_new(k,:) = qtpoula(quat)';PwbSav(k,:) = Pwb';
endfunction [Qk_plus1] = attitude_update_RK4(Qk,dt,gyro0,gyro1)
%% /*gyro0代表k-1时刻的角速度，gyro1代表k时刻的角速度*/% RK4% conference: A Robust and Easy to implement method for imu% calibration without External Equipmentsq_1=Qk;k1=(1/2)*omegaMatrix(gyro0)*q_1;q_2=Qk+dt*(1/2)*k1;k2=(1/2)*omegaMatrix((1/2)*(gyro0+gyro1))*q_2;q_3=Qk+dt*(1/2)*k2;k3=(1/2)*omegaMatrix((1/2)*(gyro0+gyro1))*q_3;q_4=Qk+dt*k3;k4=(1/2)*omegaMatrix(gyro1)*q_4;Qk_plus1=Qk+dt*(k1/6+k2/3+k3/3+k4/6);Qk_plus1=Qk_plus1/norm(Qk_plus1);
end
function [omega]=omegaMatrix(data)% wx=data(1)*pi/180;% wy=data(2)*pi/180;% wz=data(3)*pi/180;wx=data(1);wy=data(2);wz=data(3);omega=[0  , -wx , -wy , -wz ;...wx ,  0  ,  wz , -wy ;...wy , -wz ,  0  ,  wx ;...wz ,  wy , -wx ,  0   ];
end

2. 欧拉积分：

for k = 1:Nw =   imu_data(4:6, k);a =   imu_data(1:3, k);Ow = [0     -w(1)   -w(2)    -w(3);...w(1)   0       w(3)    -w(2);...w(2)  -w(3)    0        w(1);...w(3)   w(2)   -w(1)     0  ];Fc = 0.5*Ow;F = eye(4) + Fc*dt;%%或者在这里改变积分的方法(对于矩阵的积分方法)%%R_S_n = quat2dcm(quat');%%Rbwacc_w = R_S_n' * a + gw;quat = F* quat;quat = quat/norm(quat);Vw = Vw + acc_w * dt;Pwb = Pwb + Vw * dt + 0.5 * dt * dt * acc_w;
%%quatAll(k,:) = quat';oula_new(k,:) = qtpoula(quat)';PwbSav(k,:) = Pwb';
end

3. 中值积分

for k = 2:Nw = (imu_data(4:6, k-1)    +    imu_data(4:6, k))/2;a = imu_data(1:3, k-1);a1 = imu_data(1:3, k);Ow = [0     -w(1)   -w(2)    -w(3);...w(1)   0       w(3)    -w(2);...w(2)  -w(3)    0        w(1);...w(3)   w(2)   -w(1)     0  ];Fc = 0.5*Ow;F = eye(4) + Fc*dt;%%或者在这里改变积分的方法(对于矩阵的积分方法)quat1 = F* quat;%%R_S_n = quat2dcm(quat');R_S_n_1 = quat2dcm(quat1');acc_w = (R_S_n' * a + gw   +   R_S_n_1' * a1 + gw)/2;quat = F* quat;Pwb = Pwb + Vw * dt + 0.5 * dt * dt * acc_w;Vw = Vw + acc_w * dt;
%%quatAll(k,:) = quat';oula_new(k,:) = qtpoula(quat)';PwbSav(k,:) = Pwb';
end

2.2 结果

1. 欧拉积分
   
2. 中值积分
   
3. 龙格－库塔
   

---

1. https://blog.csdn.net/chenshiming1995/article/details/105107578 ↩︎

2. A Robust and Easy to Implement Method for IMU Calibration without External Equipments ↩︎

3. 参考 贺一家「从0开始写VIO」 ↩︎