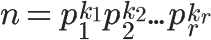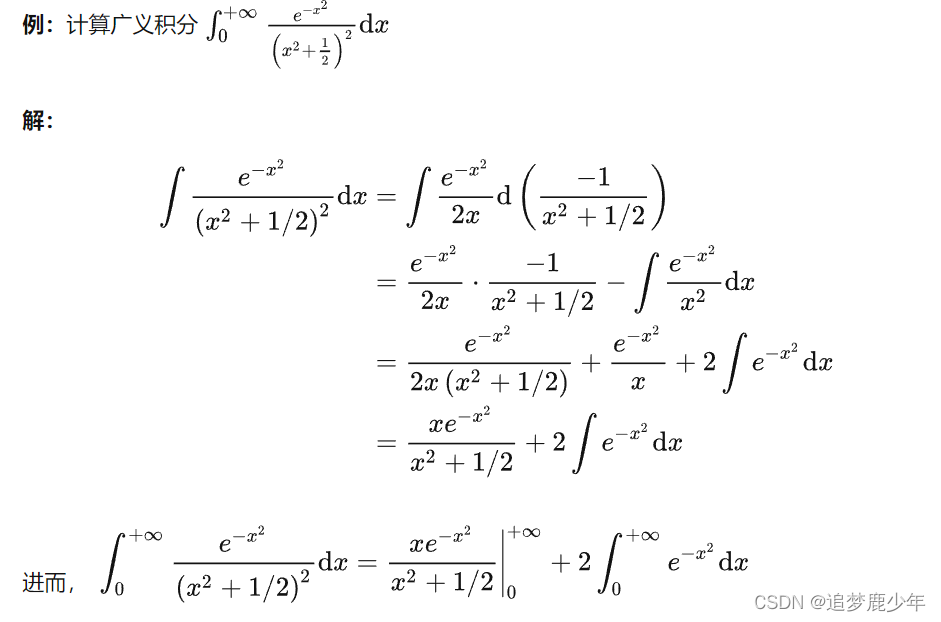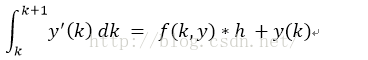1. 创建临时对象/新对象

2. 绑定原型

3. 指定 this = 临时对象

4. 执行构造函数

5. 返回临时

参考借鉴其他博客非原创，总结下，以制作一个策略类战争游戏为例，玩家可以操作一堆士兵攻击敌方。

我们着重来研究一下这个游戏里面的「制造士兵」环节。

一个士兵的在计算机里就是一堆属性，如下图：

我们只需要这样就可以制造一个士兵：

var 士兵 = {ID: 1, // 用于区分每个士兵兵种:"美国大兵",攻击力:5,生命值:42, 行走:function(){ /*走俩步的代码*/},奔跑:function(){ /*狂奔的代码*/  },死亡:function(){ /*Go die*/    },攻击:function(){ /*糊他熊脸*/   },防御:function(){ /*护脸*/       }
}兵营.制造(士兵)

制造一百个士兵

如果需要制造 100 个士兵怎么办呢？

循环 100 次吧：

var 士兵们 = []
var 士兵
for(var i=0; i<100; i++){士兵 = {ID: i, // ID 不能重复兵种:"美国大兵",攻击力:5,生命值:42, 行走:function(){ /*走俩步的代码*/}，奔跑:function(){ /*狂奔的代码*/  },死亡:function(){ /*Go die*/    },攻击:function(){ /*糊他熊脸*/   },防御:function(){ /*护脸*/       }}士兵们.push(士兵)
}兵营.批量制造(士兵们)

哎呀好简单。

质疑

上面的代码存在一个问题：浪费了很多内存。

1. 行走、奔跑、死亡、攻击、防御这五个动作对于每个士兵其实是一样的，只需要各自引用同一个函数就可以了，没必要重复创建 100 个行走、100个奔跑……
2. 这些士兵的兵种和攻击力都是一样的，没必要创建 100 次。
3. 只有 ID 和生命值需要创建 100 次，因为每个士兵有自己的 ID 和生命值。

改进

看过我们的专栏以前文章（JS 原型链）的同学肯定知道，用原型链可以解决重复创建的问题：我们先创建一个「士兵原型」，然后让「士兵」的 __proto__ 指向「士兵原型」

var 士兵原型 = {兵种:"美国大兵",攻击力:5,行走:function(){ /*走俩步的代码*/}，奔跑:function(){ /*狂奔的代码*/  },死亡:function(){ /*Go die*/    },攻击:function(){ /*糊他熊脸*/   },防御:function(){ /*护脸*/       }
}
var 士兵们 = []
var 士兵
for(var i=0; i<100; i++){士兵 = {ID: i, // ID 不能重复生命值:42}/*实际工作中不要这样写，因为 __proto__ 不是标准属性*/士兵.__proto__ = 士兵原型 士兵们.push(士兵)
}兵营.批量制造(士兵们)

优雅？

有人指出创建一个士兵的代码分散在两个地方很不优雅，于是我们用一个函数把这两部分联系起来：

function 士兵(ID){var 临时对象 = {}临时对象.__proto__ = 士兵.原型临时对象.ID = ID临时对象.生命值 = 42return 临时对象
}士兵.原型 = {兵种:"美国大兵",攻击力:5,行走:function(){ /*走俩步的代码*/}，奔跑:function(){ /*狂奔的代码*/  },死亡:function(){ /*Go die*/    },攻击:function(){ /*糊他熊脸*/   },防御:function(){ /*护脸*/       }
}// 保存为文件：士兵.js

然后就可以愉快地引用「士兵」来创建士兵了：

var 士兵们 = []
for(var i=0; i<100; i++){士兵们.push(士兵(i))
}兵营.批量制造(士兵们)

JS 之父的关怀

JS 之父创建了 new 关键字，可以让我们少写几行代码：

只要你在士兵前面使用 new 关键字，那么可以少做四件事情：

1. 不用创建临时对象，因为 new 会帮你做（你使用「this」就可以访问到临时对象）；
2. 不用绑定原型，因为 new 会帮你做（new 为了知道原型在哪，所以指定原型的名字为 prototype）；
3. 不用 return 临时对象，因为 new 会帮你做；
4. 不要给原型想名字了，因为 new 指定名字为 prototype。

这一次我们用 new 来写

function 士兵(ID){this.ID = IDthis.生命值 = 42
}士兵.prototype = {兵种:"美国大兵",攻击力:5,行走:function(){ /*走俩步的代码*/},奔跑:function(){ /*狂奔的代码*/  },死亡:function(){ /*Go die*/    },攻击:function(){ /*糊他熊脸*/   },防御:function(){ /*护脸*/       }
}// 保存为文件：士兵.js

然后是创建士兵（加了一个 new 关键字）：

var 士兵们 = []
for(var i=0; i<100; i++){士兵们.push(new 士兵(i))
}兵营.批量制造(士兵们)

new 的作用，就是省那么几行代码。（也就是所谓的语法糖）

注意 constructor 属性

new 操作为了记录「临时对象是由哪个函数创建的」，所以预先给「士兵.prototype」加了一个 constructor 属性：

士兵.prototype = {constructor: 士兵
}

如果你重新对「士兵.prototype」赋值，那么这个 constructor 属性就没了，所以你应该这么写：

士兵.prototype.兵种 = "美国大兵"
士兵.prototype.攻击力 = 5
士兵.prototype.行走 = function(){ /*走俩步的代码*/}
士兵.prototype.奔跑 = function(){ /*狂奔的代码*/  }
士兵.prototype.死亡 = function(){ /*Go die*/    }
士兵.prototype.攻击 = function(){ /*糊他熊脸*/   }
士兵.prototype.防御 = function(){ /*护脸*/       }

或者你也可以自己给 constructor 重新赋值：

士兵.prototype = {constructor: 士兵,兵种:"美国大兵",攻击力:5,行走:function(){ /*走俩步的代码*/},奔跑:function(){ /*狂奔的代码*/  },死亡:function(){ /*Go die*/    },攻击:function(){ /*糊他熊脸*/   },防御:function(){ /*护脸*/       }
}

完。