Logistic回归学习线路

预备知识：建议先去B站学习一下信息量，熵，BL散度，交叉熵的概念。

推荐B站视频：“交叉熵”如何做损失函数？打包理解“信息量”、“比特”、“熵”、“KL散度”、“交叉熵”

信息量（Information）指的是一个事件所包含的信息的多少，通常用以2为底的对数表示。比如说，如果一个事件发生的概率是1/8，那么这个事件的信息量就是log2(1/8)=-3，因为需要三个比特才能表示它。

熵（Entropy）是一个系统或信源中不确定性的度量，也可以理解为信息的平均量。在信息论中，熵越大表示系统或信源越难以预测，因此包含的信息越多。比如说，一堆硬币正反面朝上的情况有很多种可能性，因此它们的熵比一堆已知全是正面朝上的硬币要高。

KL散度（Kullback-Leibler
divergence），又称相对熵，是衡量两个概率分布之间差异的一种方式。KL散度是非负的，并且当且仅当两个分布完全相同时取值为0。

交叉熵（Cross-entropy）是一种用来比较两个概率分布之间差异的方法，它通常用于评估分类模型的性能。与KL散度类似，交叉熵也是非负的，当且仅当两个分布相等时取值为0。

本节知识导图

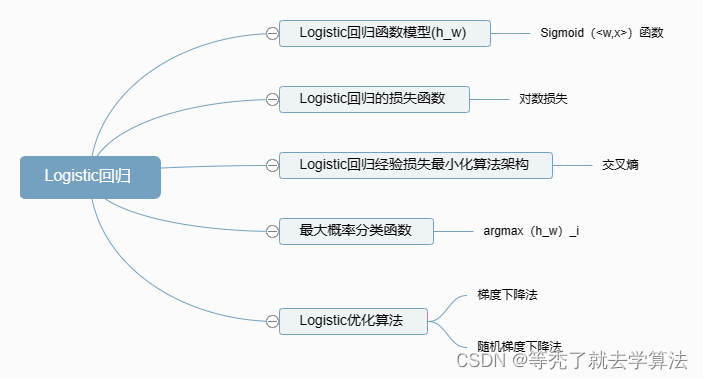
Logistic回归的函数模型

 逻辑回归是一个分类模型

 它可以用来预测某件事发生是否能够发生。分类问题是生活中最常见的问题：

• 生活中：比如预测上证指数明天是否会上涨，明天某个地区是否会下雨，西瓜是否熟了

• 金融领域：某个交易是否涉嫌违规，某个企业是否目前是否违规，在未来一段时间内是否会有违规

• 互联网：用户是否会购买某件商品，是否会点击某个内容

 对于已知的结果，上面问题的回答只有：0，1 。

 我们以以下的一个二分类为例，对于一个给定的数据集，存在一条直线可以将整个数据集分为两个部分：

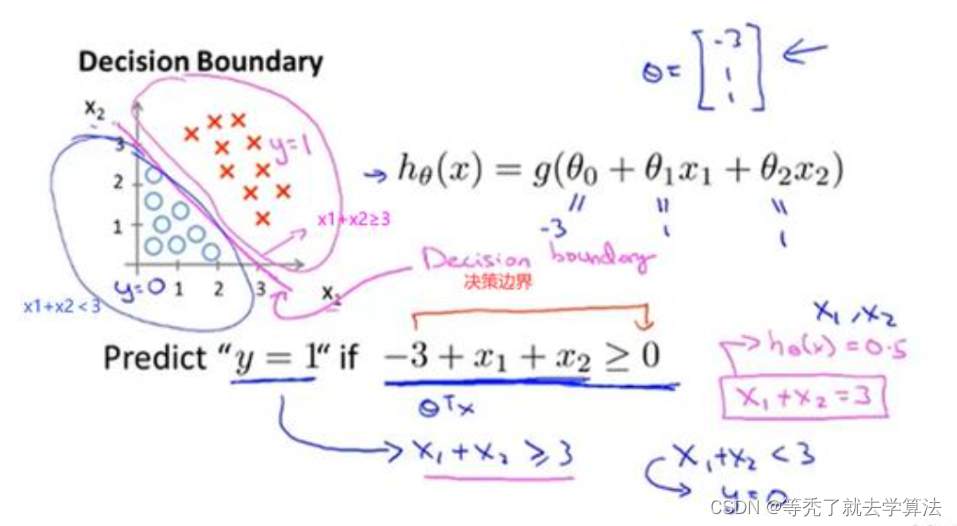
 此时，决策边界为$w_1{x}_1+w_2{x}_2+b=0$，此时我们很容易将$$h(x)=w_1{x}_1+w_2{x}_2+b>0$$的样本设置为1，反之设置为0。但是这其实是一个感知机的决策过程。
 逻辑回归在此基础上还需要在加上一层，找到分类概率与输入变量之间的关系，通过概率来判断类别。
回顾一下线性回归模型：$$h(x)=w^{T}x+b$$在线性模型的基础上加上一个函数$g$，即$h(x)=g(w^{T}x+b)$。这个函数就是sigmoid函数，也叫做logistic函数$$g(z)=\frac{1}{1+e^{-z}}$$

它可以将一个线性回归中的结果转化为一个概率值。此时$h(x)$表示的就是某件事发生的概率，我们也可以记为$p(Y=1|x)$
可以看下sigmoid函数的图像：

总结：这样，我们便得到Logistic模型$h(x)$的表达式$$h(x)=\frac{1}{1+e^{-w^{T}x+b}}$$
:$h(x_i)$的意义在于 样本$x_i$的标签为1的概率为$h(x)$

损失函数、损失最小化架构

对数损失作为损失函数

对数损失：$$l(y,\hat{y})=-\sum _{i=1}^m{y}_{i}lo{g}_2\hat{y}$$

当$l$取最小值的时候，模型$\hat{y}$分布最接近真实（理论）模型$y_i$分布

损失最小化架构

因为是二分类问题，所以

将其带入对数损失函数$l$
所以二分类的损失最小化架构为：

$$min-\sum [y_{i}log(h(x_i))+(1-y_i)log(1-h(x_i))]$$

逻辑回归损失函数为什么不用最小二乘法？答案

---

这就是交叉熵：
$$-\sum [y_{i}log(h(x_i))+(1-y_i)log(1-h(x_i))]$$

---

从概率论、统计学角度来看损失最小化架构（交叉熵）：
 在统计学中，假设我们已经有了一组样本(X,Y)，为了计算出能够产生这组样本的参数。通常我们会采用最大似然估计的方法(一种常用的参数估计的方法)。使用到最大似然估计的话，我们还要一个假设估计，这里我们就是假设 $Y$是服从于伯努利分布的。$$P(Y=1|x)=p(x)$$$$P(Y=0|x)=1-p(x)$$由于$Y$服从于伯努利分布，我们很容易就有似然函数：$$L=\prod [p(x_i{)}^{y_i}][1-p(x_i){]}^{(1-y_i)}$$为了求解我们可以两边取对数：
$$logL=\sum [y_{i}log(p(x_i))+(1-y_i)log(1-p(x_i))]$$

最大似然估计其实就是取概率的概率最大的那个概率模型：这么说你可能不懂，换种方式，$\prod p(h(x_i)|\theta )$,已有概率模型$h(x)$在现有样本$\theta$的条件下，计算出值越大,越说明$h(x)$最接近理论概率模型

我们一般喜欢取式子的最小值，所以将原式子转化一下
$$min(-logL)=min-\sum [y_{i}log(p(x_i))+(1-y_i)log(1-p(x_i))]$$

这里的$p(x_i)$对应的就是$h(x_i)$

从信息量，熵的角度来看损失最小化架构：

KL散度：当$D_{KL}=0$时，P模型=Q模型，我们追求的就是我们所构建的Q模型（也就是$h(x)$）接近真实P模型(这里是样本的理论模型,$p_i为$样本)

没错，根据吉布斯不等式，交叉熵$\ge$ P系统的熵，所以当我们取交叉熵的最小值时，Q模型越接近真实的理论P模型，又知道，信息量的定义是$$f:=-lo{g}_{2}x$$
所以带入原式子,交叉熵为：$$-\sum _{i=1}^m{p}_{i}lo{g}_{2}x$$

这也就是对数损失的由来：$$l(y,\hat{y})=-\sum _{i=1}^m{y}_{i}lo{g}_2\hat{y}$$看老师的课的时候，直接丢给我一个对数损失，然后又直接讲交叉熵，对数损失为啥可以作为损失函数，也没告诉我们。通过上面的知识，读者应该明白这个对数损失怎么来的了吧。继续看下去，你会收获更多。

推荐视频：[“交叉熵”如何做损失函数？打包理解“信息量”、“比特”、“熵”、“KL散度”、“交叉熵”]

因为是二分类问题，所以

所以二分类的交叉熵为：

$$-\sum [y_{i}log(p(x_i))+(1-y_i)log(1-p(x_i))]$$

这里的$p(x_i)$对应的就是$h(x_i)$

这两个角度的思考：

• 它们推导出来的式子是一样的，是不是都能叫交叉熵？
  • 不是的，它们只是式子相同，最大似然估计函数推导的时候是因为习惯上将相乘改为相加，所以才出现的$log$，它的底数可以为任意正数，而且没有单位，而信息量将$lo{g}_2$写进了定义里，并且他是有单位的，比特就是它的单位。

分类函数

最大概率分类函数

在一个$k$元分类问题中，给定预测概率模型$h$，即
$$h(x)=(h_1(x),h_2(x),...,h_k(x))$$其中，$h_i(x)$是样本属于第i个类别的概率。
关于模型h的最大概率分类函数为：
$$MaxPro{b}_h(x)=argmax{h}_i(x)$$

:argmax，取最大值的下标。
这个$h_i(x)$可以理解为，样本标签为$h_i$的概率，最大$h_i$的作为样本i的标签

阈值分类函数

在一个2元分类问题中，设标签在{0,1}中取值。
给定预测概率模型h，即h(x)表示特征组x的标签为1的概率。
关于模型h的以t为阈值的阈值分类函数为：

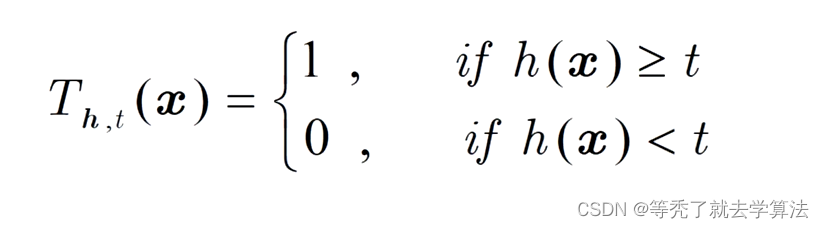
其就是，如果真实标签为1，那么就是当预测模型（标签为1）函数值大于某个值的时候，便认为预测标签为1，反正为0

Logistic回归的优化算法

梯度下降

理论部分：我的另一篇文章：搜索算法—学习笔记

achine_learning.logistic_regression.lib.logistic_regression_gd
import numpy as npdef sigmoid(scores):return 1 / (1 + np.exp(-scores))class LogisticRegression:def fit(self, X, y, eta=0.1, N = 1000): #eta ηm, n = X.shapew = np.zeros((n,1))for t in range(N):h = sigmoid(X.dot(w)) #hw(X)g = 1.0 / m * X.T.dot(h - y) #梯度gw = w - eta * g #更新wself.w = wdef predict_proba(self, X):return sigmoid(X.dot(self.w)) # 概率def predict(self, X):proba = self.predict_proba(X) # 概率return (proba >= 0.5).astype(np.int) 

交叉熵是一个凸函数吗，可导。

随机梯度下降

理论部分：我的另一篇文章：搜索算法—学习笔记

import numpy as npdef sigmoid(scores):return 1.0 / (1 + np.exp(-scorecs ))class LogisticRegression:def fit(self, X, y, eta_0=10, eta_1=50, N=1000):m, n = X.shapew = np.zeros((n,1))self.w = wfor t in range(N):i = np.random.randint(m) #随机选一个样本 x(i)x = X[i].reshape(1, -1) # 1*n 向量pred = sigmoid(x.dot(w)) # hw(x)g = x.T * (pred - y[i]) # 梯度w = w - eta_0 / (t + eta_1) * g # 更新wself.w += wself.w /= N # w均值def predict_proba(self, X):return sigmoid(X.dot(self.w))def predict(self, X):proba = self.predict_proba(X)return (proba >= 0.5).astype(np.int)

小批量梯度下降

坐标下降