1．实验目标

算法：DBScan，基于密度的聚类算法

输入：

D：一个包含n个数据的数据集

r：半径参数

minPts：领域密度阈值

输出：基于密度的聚类集合

2．实验步骤

标记D中所有的点为unvisted

foreachpinD

ifp.visit = unvisted

找出与点p距离不大于r的所有点集合N

IfN.size() < minPts

标记点p为噪声点

Else

foreachp' in N

Ifp'.visit == unvisted

找出与点p距离不大于r的所有点集合N'

IfN'.size()>=minPts

将集合N'加入集合N中去

Endif

Else

Ifp'未被聚到某个簇

将p'聚到当前簇

Ifp'被标记为噪声点

将p'取消标记为噪声点

EndIf

EndIf

EndIf

Endfor

Endif

Endif

Endfor

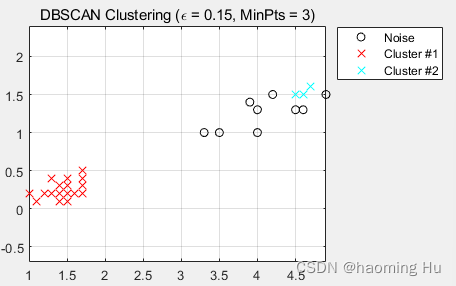
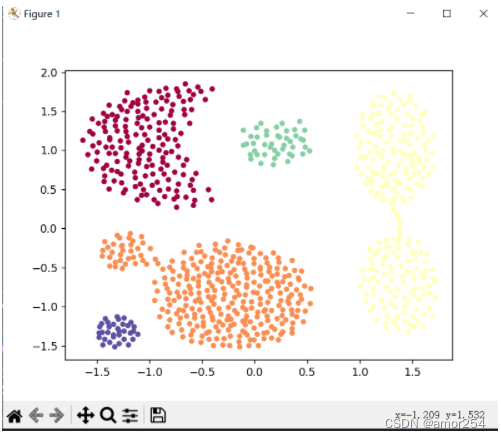
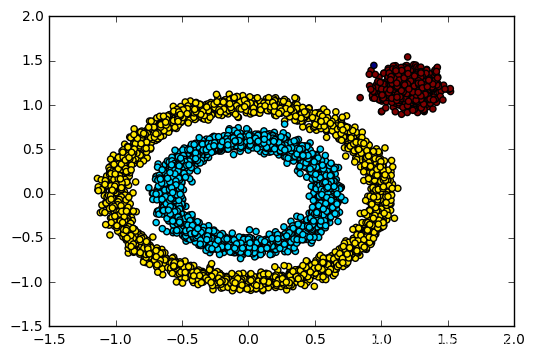
3．实验结果

 

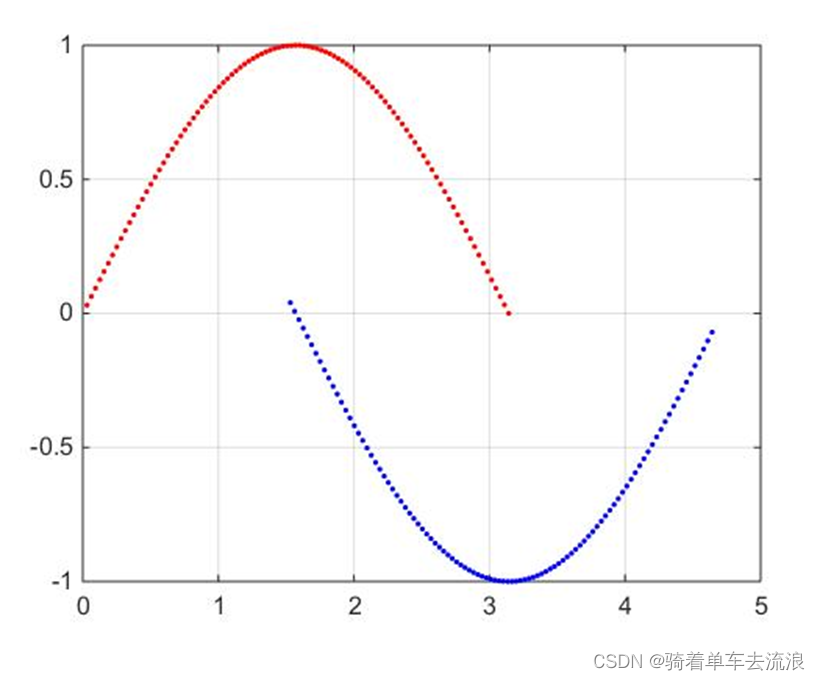
4、实验结果

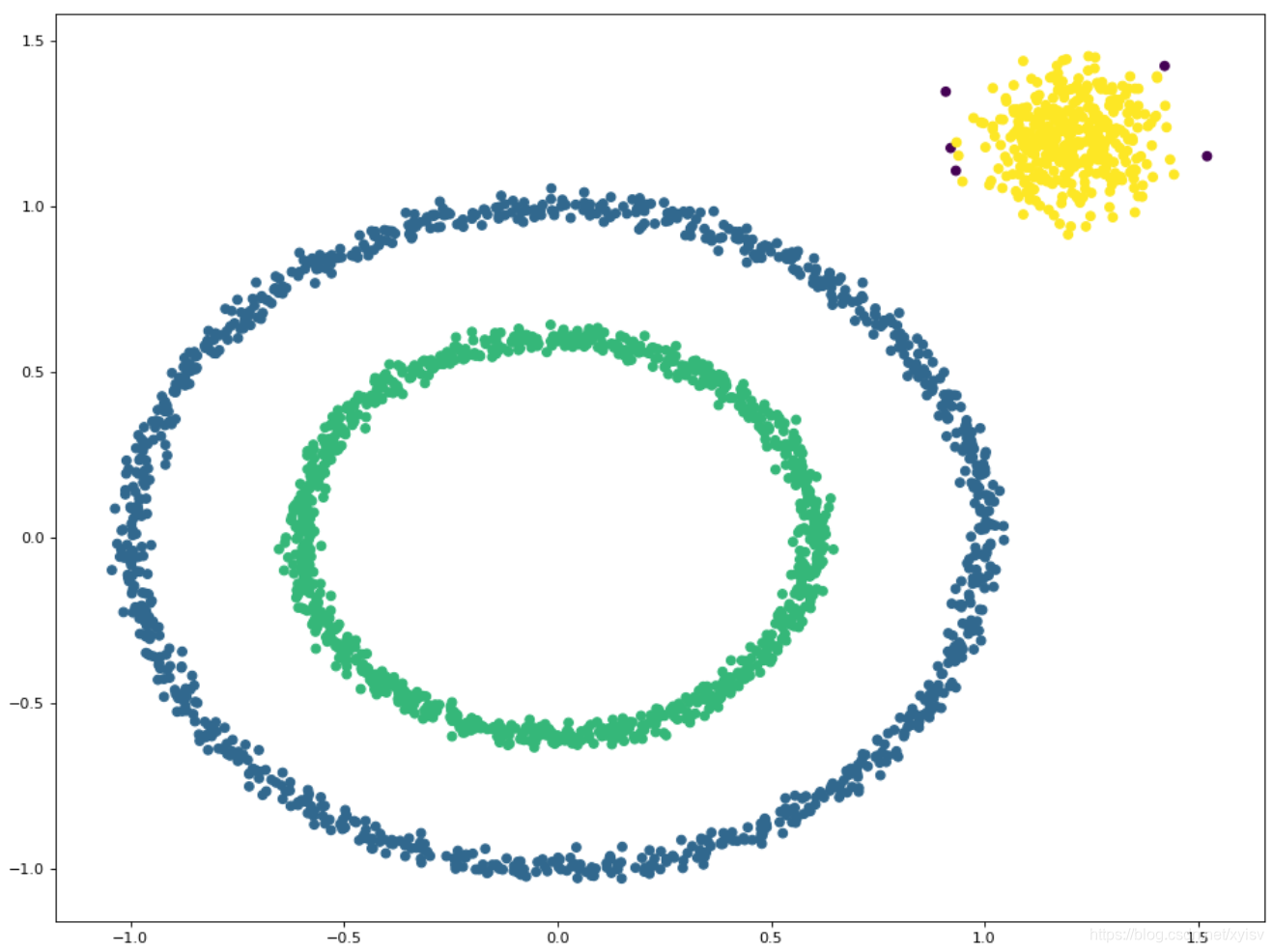
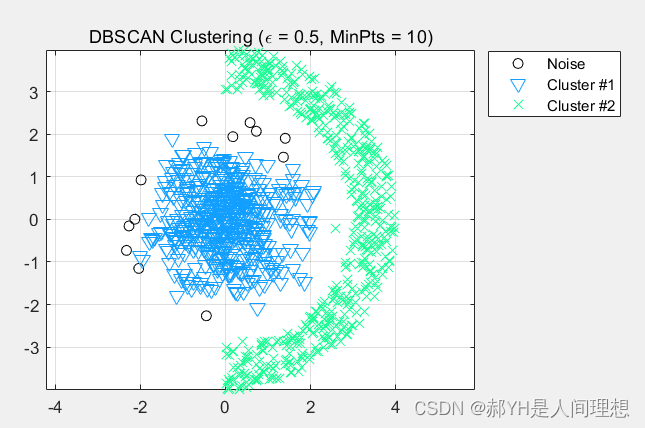
和传统的K-Means算法相比，DBSCAN最大的不同就是不需要输入类别数k，当然它最大的优势是可以发现任意形状的聚类簇，而不是像K-Means，一般仅仅使用于凸的样本集聚类。同时它在聚类的同时还可以找出异常点，这点和BIRCH算法类似。

　　那么我们什么时候需要用DBSCAN来聚类呢？一般来说，如果数据集是稠密的，并且数据集不是凸的，那么用DBSCAN会比K-Means聚类效果好很多。如果数据集不是稠密的，则不推荐用DBSCAN来聚类。

　　　　下面对DBSCAN算法的优缺点做一个总结。

　　　　DBSCAN的主要优点有：

　　　　1） 可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。

　　　　2） 可以在聚类的同时发现异常点，对数据集中的异常点不敏感。

　　　　3） 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

　　　　DBSCAN的主要缺点有：

　　　　1）如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。

　　　　2） 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。

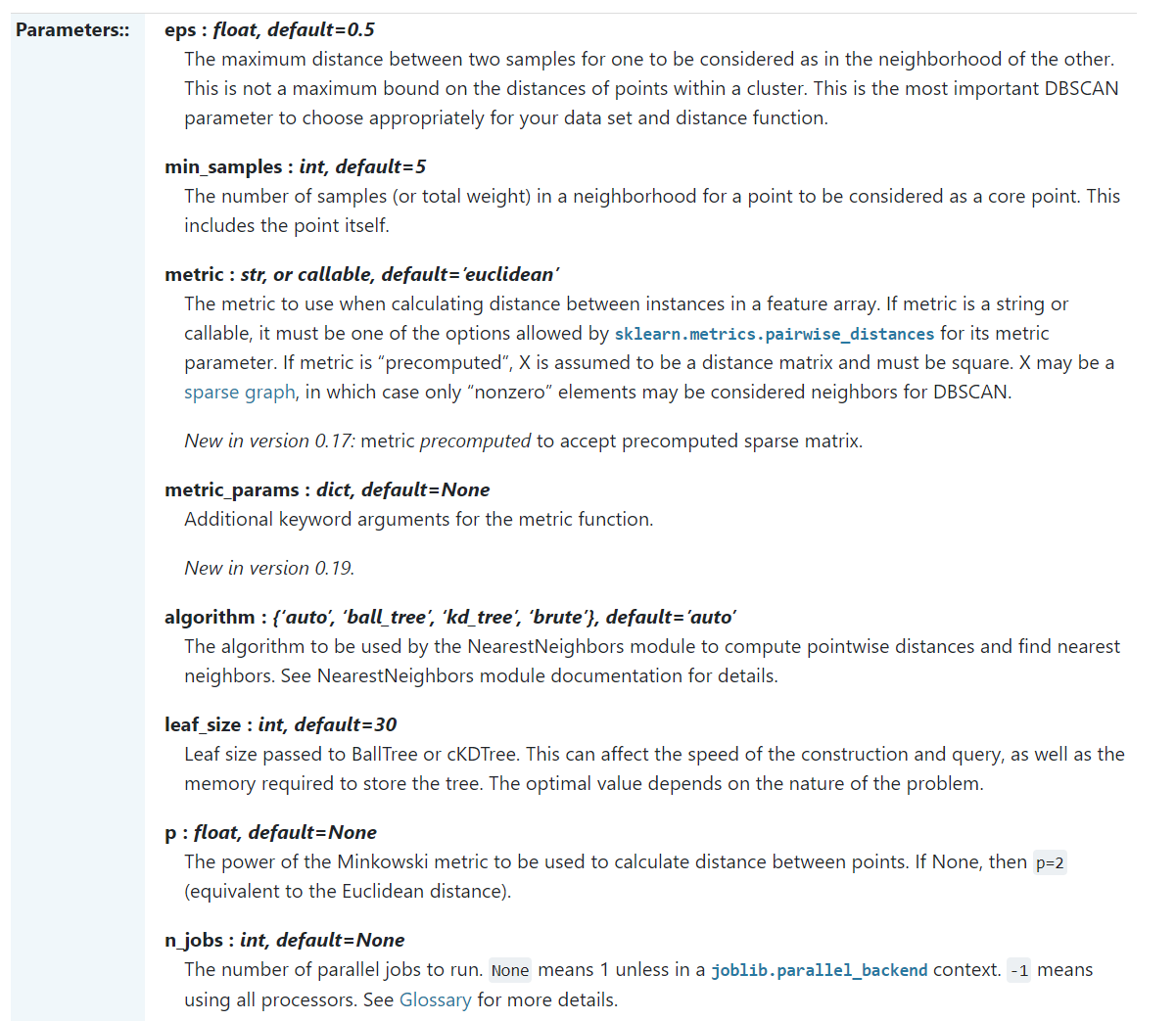
　　　　3） 调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵ，邻域样本数阈值MinPts联合调参，不同的参数组合对最后的聚类效果有较大影响。