一、原理

参考博文：

DBSCAN聚类算法Python实现_徐奕的专栏-CSDN博客_dbscan pythonhttps://blog.csdn.net/xyisv/article/details/88918448DBSCAN是一种基于密度的聚类算法，这类密度聚类算法一般假定类别可以通过样本分布的紧密程度决定。同一类别的样本，他们之间的紧密相连的，也就是说，在该类别任意样本周围不远处一定有同类别的样本存在。
通过将紧密相连的样本划为一类，这样就得到了一个聚类类别。通过将所有各组紧密相连的样本划为各个不同的类别，则我们就得到了最终的所有聚类类别结果。

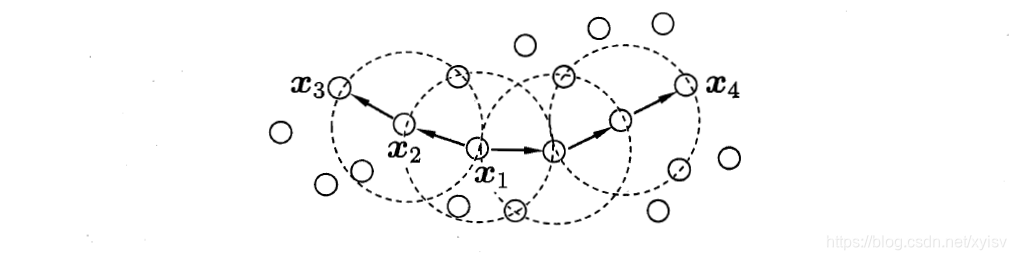
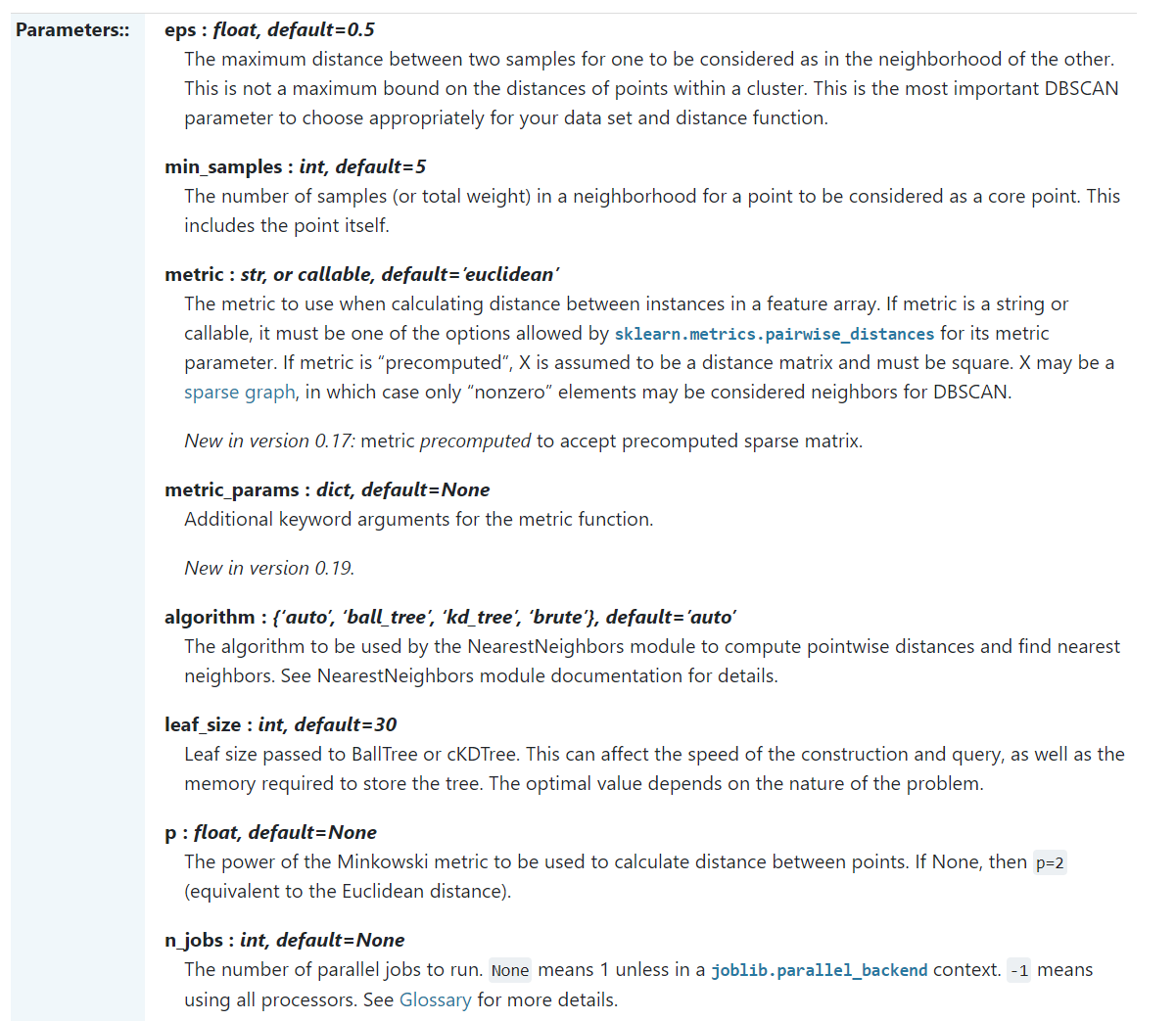
x1是核心对象，x2由x1密度直达，x3由x1密度可达，x3与x4密度相连 

 二、Python实战

参考链接： 

从零开始学Python【31】—DBSCAN聚类（实战部分） - 云+社区 - 腾讯云 (tencent.com)https://cloud.tencent.com/developer/article/1480298在Python的sklearn模块中，cluster子模块集成了常用的聚类算法，如K均值聚类、密度聚类和层次聚类等。对于密度聚类而言，读者可以直接调用cluster子模块中的DBSCAN“类”，有关该“类”的语法和参数含义如下：

cluster.DBSCAN(eps=0.5, min_samples=5, metric='euclidean',metric_params=None, algorithm='auto',leaf_size=30, p=None, n_jobs=1)
eps：用于设置密度聚类中的ε领域，即半径，默认为0.5；
min_samples：用于设置ε领域内最少的样本量，默认为5；
metric：用于指定计算点之间距离的方法，默认为欧氏距离；
metric_params：用于指定metric所对应的其他参数值；
algorithm：在计算点之间距离的过程中，用于指点搜寻最近邻样本点的算法；默认为'auto'，表示密度聚类会自动选择一个合适的搜寻方法；如果为'ball_tree'，则表示使用球树搜寻最近邻；如果为'kd_tree'，则表示使用K-D树搜寻最近邻；如果为'brute'，则表示使用暴力法搜寻最近邻；
leaf_size：当参数algorithm为'ball_tree'或'kd_tree'时，用于指定树的叶子节点中所包含的最多样本量，默认为30；该参数会影响搜寻树的构建和搜寻最近邻的速度；
p：当参数metric为闵可夫斯基距离时（'minkowski'），p=1，表示计算点之间的曼哈顿距离；p=2，表示计算点之间的欧氏距离；该参数的默认值为2；
n_jobs：用于设置密度聚类算法并行计算所需的CPU数量，默认为1表示仅使用1个CPU运行算法，即不使用并行运算功能；

需要说明的是，在DBSCAN“类”中，参数eps和min_samples需要同时调参，即通常会指定几个候选值，并从候选值中挑选出合理的阈值；在参数eps固定的情况下，如果参数min_samples越大，所形成的核心对象就越少，往往会误判出许多异常点，聚成的簇数目也会增加，反之，会产生大量的核心对象，导致聚成的簇数目减少；在参数min_samples固定的情况下，参数eps越大，就会导致更多的点落入到ε领域内，进而使核心对象增多，最终使聚成的簇数目减少，反之，会导致核心对象大量减少，最终聚成的簇数目增多。在参数eps和min_samples不合理的情况下，簇数目的增加或减少往往都是错误的，例如应该聚为一类的样本由于簇数目的增加而聚为多类；不该聚为一类的样本由于簇数目的减少而聚为一类。 

实战一

参考链接：

Python与机器学习：DBSCAN聚类 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/54833132 

import numpy as np
from sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets._samples_generator import make_blobs
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import seaborn as sns  #可视化库# 生成聚类中心点
centers = [[1, 1], [-1, -1], [1, -1]] 
# 生成样本数据集
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4,random_state=0)
#画布设置
fig = plt.figure(figsize=(12,5))
fig.subplots_adjust(left=0.02, right=0.98, bottom=0.05, top=0.9)
ax = fig.add_subplot(1,2,1)
row, _ = np.shape(X)
#画子图，未聚类点
for i in range(row):ax.plot(X[i, 0], X[i, 1], '#4EACC5', marker='.')# StandardScaler 标准化处理。且是针对每一个特征维度来做的，而不是针对样本。
X = StandardScaler().fit_transform(X)
# 调用密度聚类  DBSCAN
db = DBSCAN(eps=0.3, min_samples=10).fit(X)
# print(db.labels_)  # db.labels_为所有样本的聚类索引，没有聚类索引为-1
# print(db.core_sample_indices_) # 所有核心样本的索引core_samples_mask = np.zeros_like(db.labels_, dtype=bool)  # 设置一个样本个数长度的全false向量
core_samples_mask[db.core_sample_indices_] = True #将核心样本部分设置为true
labels = db.labels_n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
# 获取聚类个数。（聚类结果中-1表示没有聚类为离散点）# 模型评估
print('估计的聚类个数为: %d' % n_clusters_)
print("同质性: %0.3f" % metrics.homogeneity_score(labels_true, labels))  # 每个群集只包含单个类的成员。
print("完整性: %0.3f" % metrics.completeness_score(labels_true, labels))  # 给定类的所有成员都分配给同一个群集。
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))  # 同质性和完整性的调和平均
print("调整兰德指数: %0.3f" % metrics.adjusted_rand_score(labels_true, labels))
print("调整互信息: %0.3f" % metrics.adjusted_mutual_info_score(labels_true, labels))
print("轮廓系数: %0.3f" % metrics.silhouette_score(X, labels))sns.set(font='SimHei',style='ticks')unique_labels = set(labels)
colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]ax = fig.add_subplot(1,2,2)
for k, col in zip(unique_labels, colors):if k == -1:  # 聚类结果为-1的样本为离散点# 使用黑色绘制离散点col = [0, 0, 0, 1]class_member_mask = (labels == k)  # 将所有属于该聚类的样本位置置为truexy = X[class_member_mask & core_samples_mask]  # 将所有属于该类的核心样本取出，使用大图标绘制ax.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),markeredgecolor='k', markersize=14)xy = X[class_member_mask & ~core_samples_mask]  # 将所有属于该类的非核心样本取出，使用小图标绘制ax.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),markeredgecolor='k', markersize=6)plt.title('Estimated number of clusters: %d' % n_clusters_)
sns.despine()
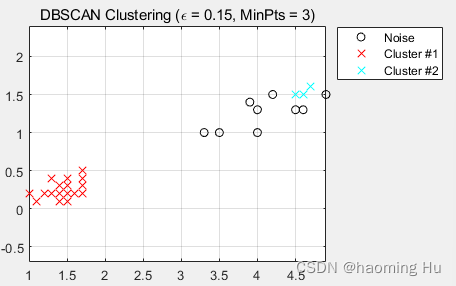
plt.show()

估计的聚类个数为: 3
同质性: 0.953
完整性: 0.883
V-measure: 0.917
调整兰德指数: 0.952
调整互信息: 0.916
轮廓系数: 0.626

 其中调整兰德指数用来衡量两个分布的吻合程度，值越大意味着聚类结果与真实情况越吻合，取值范围[-1,1]，数值越接近于1，表示聚类效果越好。

实验图：

 实战二

 参考链接：DBSCAN聚类算法Python实现_徐奕的专栏-CSDN博客_dbscan pythonhttps://blog.csdn.net/xyisv/article/details/88918448

from sklearn import datasets
import numpy as np
import random
import matplotlib.pyplot as plt
import time
import copy#def定义函数+函数名(参数)，返回值:return()
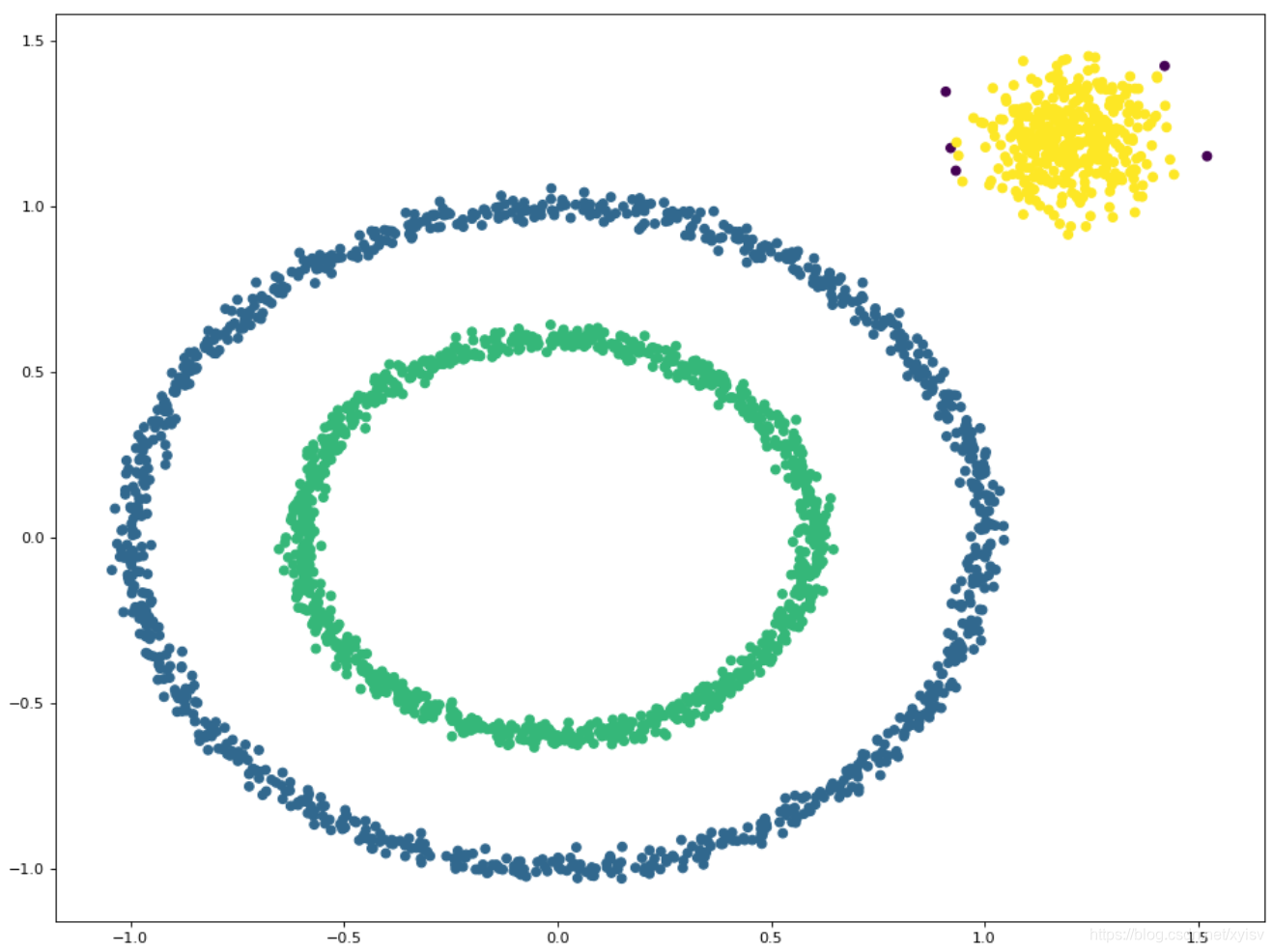
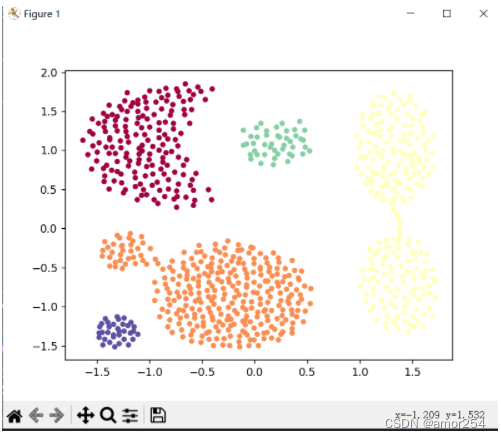
def find_neighbor(j, x, eps):N = list()for i in range(x.shape[0]):temp = np.sqrt(np.sum(np.square(x[j] - x[i])))  # 计算欧式距离#如果距离小于epsif temp <= eps:#append用于在列表末尾添加新的对象N.append(i)#返回邻居的索引return set(N)def DBSCAN(X, eps, min_Pts):k = -1neighbor_list = []  # 用来保存每个数据的邻域omega_list = []  # 核心对象集合gama = set([x for x in range(len(X))])  # 初始时将所有点标记为未访问cluster = [-1 for _ in range(len(X))]  # 聚类for i in range(len(X)):neighbor_list.append(find_neighbor(i, X, eps))#取倒数第一个进行if，如果大于设定的样本数，即为核心点if len(neighbor_list[-1]) >= min_Pts:omega_list.append(i)  # 将样本加入核心对象集合omega_list = set(omega_list)  # 转化为集合便于操作while len(omega_list) > 0:#深复制gamagama_old = copy.deepcopy(gama)j = random.choice(list(omega_list))  # 随机选取一个核心对象#k计数，从0开始为第一个k = k + 1#初始化QQ = list()#记录访问点Q.append(j)#从gama中移除j,剩余未访问点gama.remove(j)while len(Q) > 0:#将第一个点赋值给q,Q队列输出给q,先入先出。q = Q[0]Q.remove(q)if len(neighbor_list[q]) >= min_Pts:#&按位与运算符：参与运算的两个值,如果两个相应位都为1,则该位的结果为1,否则为0delta = neighbor_list[q] & gamadeltalist = list(delta)for i in range(len(delta)):#在Q中增加访问点Q.append(deltalist[i])#从gama中移除访问点,剩余未访问点gama = gama - delta#原始未访问点-剩余未访问点=访问点Ck = gama_old - gamaCklist = list(Ck)for i in range(len(Ck)):#类型为kcluster[Cklist[i]] = k#剩余核心点omega_list = omega_list - Ckreturn cluster#创建一个包含较小圆的大圆的样本集
X1, y1 = datasets.make_circles(n_samples=2000, factor=.6, noise=.02)
#生成聚类算法的测试数据
X2, y2 = datasets.make_blobs(n_samples=400, n_features=2, centers=[[1.2, 1.2]], cluster_std=[[.1]], random_state=9)
X = np.concatenate((X1, X2))
#判断为邻居的半径
eps = 0.08
#判断为核心点的样本数
min_Pts = 10
begin = time.time()
C = DBSCAN(X, eps, min_Pts)
end = time.time()-begin
plt.figure()
plt.scatter(X[:, 0], X[:, 1], c=C)
plt.show()
print(end)
print(X)

结果图：