毫米雷达点云 DBSCAN聚类算法
- 聚类的目的
- 聚类算法分类
- 原型聚类
- 层次聚类
- 密度聚类
- DBSCAN聚类算法原理
- 相关定义
- 算法流程以及伪代码
- DBSCAN算法优缺点
- DBSCAN参数选择
- 聚类衡量指标
- DBSCAN算法仿真
- DBSCAN代码
- DBSCAN算法对毫米波雷达点云数据进行聚类
聚类的目的
聚类的目的是将一组数据点划分为具有相似特征或属性的组或簇。通过聚类分析,我们可以识别出数据中的内在模式、结构和关联关系,从而获得对数据的更深入理解。
具体来说,聚类的目的可以分为以下三部分:
-
发现数据的内在结构:
聚类可以将数据分成簇,这些簇可能表示数据的不同模式、集群或分布。通过将相似的数据点放在同一簇中,我们可以揭示数据的内在结构和组织方式。 -
数据预处理
通过将数据分成不同的簇,可以减少数据的复杂性和噪声,提取关键特征,并简化后续的数据分析任务。(比如形状特征) -
异常点剔除
聚类算法可以帮助我们识别和排除异常点或噪声数据。这些异常点可能是数据中的异常值、离群点或错误数据,对于准确的分析和建模是有害的。
聚类算法分类
现有的聚类算法可以大致分为三种,分别是
- 原型聚类(Prototype-based clustering)
- -层次聚类 (Hierarchical clustering)
- 密度聚类 (Density-based clustering)
原型聚类
该类算法的主要思想为根据给定的划分集合个数 K,将所有数据对象分配到K个集合中,每个集合中各个数据对象到本身集合中心点相似度最高相对于其他集合中心对象。 该算法主要通过迭代的方式得到最优的聚类中心点和各个聚类集合,主要适用于球状簇的发现。 常用的划分聚类算法 K-means、 CLARANs、 CLARA、PAM 等。 在数据挖掘领域被广泛应用,但是这些算法都要求在聚类之前就确定输出的簇的数量。对于汽车雷达来说,也就是要求在聚类之前就确定目标的数量,这显然是无法做到的,因为汽车雷达无法确定当前的目标数量是多少。
层次聚类
层次聚类尝试在不同层次对数据集进行划分,从而形成树形的聚类结构。层次聚类可以采用“自下而上”的聚类策略,也可以采用“自上而下”的聚类策略。AGNES 方 法 (AGglomerative NESting)是一种常用的“自下而上”的层次聚类算法。然而这种算法面临和原型聚类相同的问 题,也需要在聚类之前确定输出的簇的数量,因此也无法直接应用到汽车雷达上,因此就只剩下了密度聚类。
密度聚类
密度聚类(Density-based clustering)没有其它两种聚类的限制,不需要事先确定簇的数量。密度聚类假设簇的 结构能通过目标点分布的紧密程度来确定。在密度聚类中,簇被认为是数据空间中目标点密集的区域,在簇之间出 现的低密度的目标点被认为是噪声. 这些簇可以有任意的形状,并且簇内的目标点也可以任意分布,这一点和汽车 雷达上的检测目标特性十分接近。汽车雷达对应同一个目标的检测点之间距离接近,并且这些点的密度分布是一定 的(这个密度分布和物体的反射特性相关)。因为具备以上这些特性,密度聚类更加适合于汽车雷达的应用,DBSCAN 算法(Density-Based Spatial Clustering of Applications with Noise)是一种常用的密度聚类算法。
DBSCAN聚类算法原理
相关定义
DBSCAN是一种基于密度的聚类算法,这类密度聚类算法一般假定类别可以通过样本分布的紧密程度决定。同一类别的样本,他们之间的紧密相连的,也就是说,在该类别任意样本周围不远处一定有同类别的样本存在。
DBSCAN是基于一组邻域来描述样本集的紧密程度的,参数(ϵ, MinPts)用来描述邻域的样本分布紧密程度。其中,ϵ描述了某一样本的邻域距离阈值,MinPts描述了某一样本的距离为ϵ的邻域中样本个数的阈值。
给出算法中用到的定义:
● ϵ领域:对于 x j ∈ D x_j \in D xj∈D,其ϵ-邻域包含样本集D中与xj的距离不大于ϵ的子样本集,即 N ϵ ( x j ) = { x i ∈ D ∣ d i s t a n c e ( x i , x j ) ≤ ϵ } N_{\epsilon}(x_j) = \{x_i \in D | distance(x_i,x_j) \leq \epsilon\} Nϵ(xj)={xi∈D∣distance(xi,xj)≤ϵ},这个子样本集的个数记为 ∣ N ϵ ( x j ) ∣ |N_{\epsilon}(x_j)| ∣Nϵ(xj)∣。
● 核心对象(核心点):对于任一样本 x j ∈ D x_j \in D xj∈D,如果其ϵ-邻域对应的 ∣ N ϵ ( x j ) ∣ |N_{\epsilon}(x_j)| ∣Nϵ(xj)∣至少包含MinPts个样本,即如果 ∣ N ϵ ( x j ) ∣ ≥ M i n P t s |N_{\epsilon}(x_j)| \geq MinPts ∣Nϵ(xj)∣≥MinPts,则 x j x_j xj是一个核心对象。
● 边界点:如果 ∣ N ϵ ( x j ) ∣ < M i n P t s |N_{\epsilon}(x_j)| < MinPts ∣Nϵ(xj)∣<MinPts,则 x j x_j xj是一个边界点。
● 噪声点:既不是核心点也不是边界点的点
● 密度直达(directly density-reachable):如果 x i x_i xi位于 x j x_j xj的ϵ-邻域中,且 x j x_j xj是核心对象,那么称 x i x_i xi由 x j x_j xj密度直达。
● 密度可达(density-reachable):对于 x i x_i xi和 x j x_j xj,如果存在样本样本序列 p 1 , p 2 , . . . , p T p_1, p_2,...,p_T p1,p2,...,pT,满足 p 1 = x i , p T = x j p_1 = x_i, p_T = x_j p1=xi,pT=xj 且 p t + 1 p_{t+1} pt+1由 p t p_{t} pt密度直达,则称 x j x_j xj由 x i x_i xi密度可达。也就是说,密度可达满足传递性。此时序列中的传递样本 p 1 , p 2 , . . . , p T − 1 p_1, p_2,...,p_{T-1} p1,p2,...,pT−1均为核心对象,因为只有核心对象才能使其他样本密度直达。注意密度可达也不满足对称性,这个可以由密度直达的不对称性得出。
● 密度相连(density-connected):对于 x i x_i xi和 x j x_j xj,如果存在核心对象样本 x k x_k xk,使 x i x_i xi和 x j x_j xj均由 x k x_k xk密度可达,则称 x i x_i xi和 x j x_j xj密度相连,密度相连关系是满足对称性的。
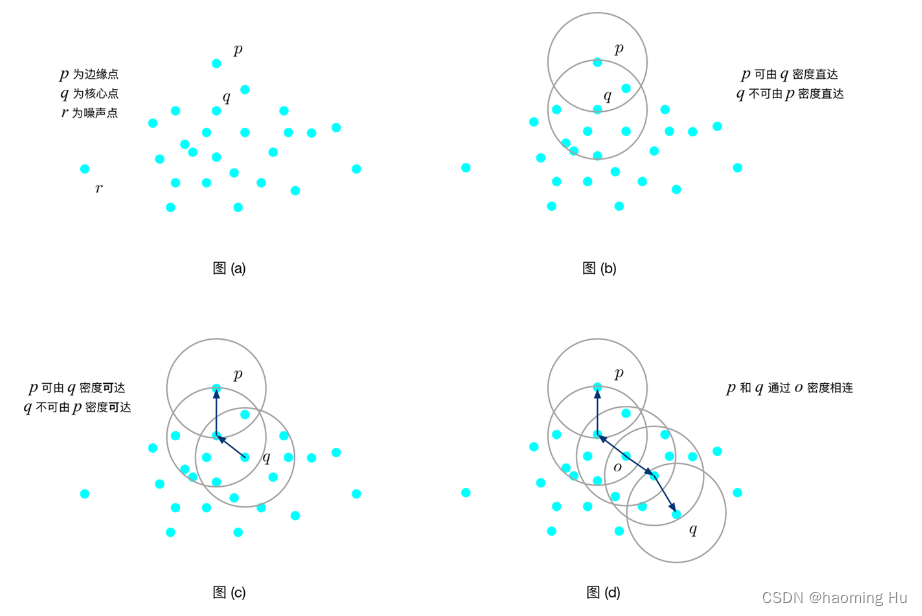
DBSCAN的聚类定义:由密度可达关系导出的最大密度相连的样本集合,即为我们最终聚类的一个类别,或者说一个簇。
算法流程以及伪代码
开始:
- 初始化所有数据点的聚类标签为未分类(unclassified)
- 初始化聚类编号为0
- 遍历每个数据点:
- 如果该数据点已经分类,则跳过
- 标记该数据点为已访问
- 找到该数据点的邻域点集合
- 如果邻域点数量小于最小邻域点数量(MinPts):
- 标记该数据点为噪声点
- 否则:
- 创建一个新的聚类
- 将该数据点及其邻域点加入聚类
- 扩展聚类:
- 对于邻域点集合中的每个点:
- 如果该点未访问:
- 标记该点为已访问
- 找到该点的邻域点集合
- 如果邻域点数量大于等于最小邻域点数量(MinPts):
- 将该点的邻域点集合加入当前聚类的邻域点集合
- 如果该点未分类:
- 将该点加入当前聚类
结束
- 将该点加入当前聚类
- 如果该点未访问:
- 对于邻域点集合中的每个点:
伪代码:
(1) 首先将数据集D中的所有对象标记为未处理状态
(2) for(数据集D中每个对象p) do
(3) if (p已经归入某个簇或标记为噪声) then
(4) continue;
(5) else
(6) 检查对象p的Eps邻域 NEps(p) ;
(7) if (NEps(p)包含的对象数小于MinPts) then
(8) 标记对象p为边界点或噪声点;
(9) else
(10) 标记对象p为核心点,并建立新簇C, 并将p邻域内所有点加入C
(11) for (NEps(p)中所有尚未被处理的对象q) do
(12) 检查其Eps邻域NEps(q),若NEps(q)包含至少MinPts个对象,则将NEps(q)中未归入任何一个簇的对象加入C;
(13) end for
(14) end if
(15) end if
(16) end for
算法流程图:
(还没画,画完就补上)
DBSCAN算法优缺点
优点:
(1)聚类速度快且能够有效处理噪声点和发现任意形状的空间聚类;
(2)与K-MEANS比较起来,不需要输入要划分的聚类个数;
(3)聚类簇的形状没有偏倚; (4)可以在需要时输入过滤噪声的参数。
缺点:
(1)当数据量增大时,要求较大的内存支持I/O消耗也很大;
(2)当空间聚类的密度不均匀、聚类间距差相差很大时,聚类质量较差,因为这种情况下参数MinPts和Eps选取困难。
(3)算法聚类效果依赖与距离公式选取,实际应用中常用欧式距离,对于高维数据,存在“维数灾难”。
DBSCAN参数选择
聚类衡量指标
DBSCAN算法仿真
DBSCAN代码
原始的DBSCAN算法参考链接:聚类方法:DBSCAN算法研究(2)–matlab代码实现
X1 =[5.1,3.5,1.4,0.2;
4.9,3.0,1.4,0.2;
4.7,3.2,1.3,0.2;
4.6,3.1,1.5,0.2;
5.1,3.7,1.5,0.4;
4.6,3.6,1.0,0.2;
5.1,3.3,1.7,0.5;
5.0,3.6,1.4,0.2;
5.4,3.9,1.7,0.4;
4.6,3.4,1.4,0.3;
5.0,3.4,1.5,0.2;
4.4,2.9,1.4,0.2;
4.9,3.1,1.5,0.1;
5.4,3.7,1.5,0.2;
4.8,3.4,1.6,0.2;
4.8,3.0,1.4,0.1;
4.3,3.0,1.1,0.1;
5.8,4.0,1.2,0.2;
5.7,4.4,1.5,0.4;
5.4,3.9,1.3,0.4;
5.1,3.5,1.4,0.3;
5.7,3.8,1.7,0.3;
5.1,3.8,1.5,0.3;
5.4,3.4,1.7,0.2;
6.4,3.2,4.5,1.5;
6.9,3.1,4.9,1.5;
5.5,2.3,4.0,1.3;
6.5,2.8,4.6,1.5;
5.7,2.8,4.5,1.3;
6.3,3.3,4.7,1.6;
4.9,2.4,3.3,1.0;
4.9,2.4,3.3,1.0;
6.6,2.9,4.6,1.3;
5.2,2.7,3.9,1.4;
5.0,2.0,3.5,1.0;
5.9,3.0,4.2,1.5;
6.0,2.2,4.0,1.0];
X=X1(:,3:4);
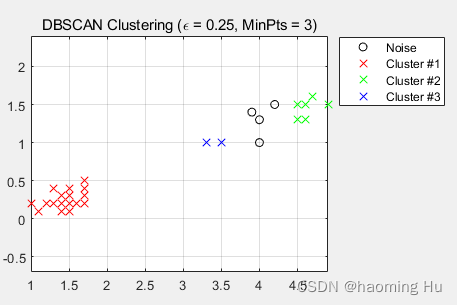
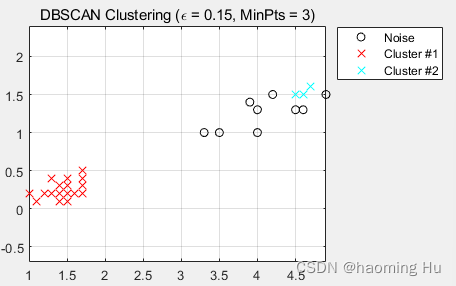
epsilon= 0.15 ;
MinPts= 3 ;
IDX1=DBSCAN(X,epsilon,MinPts);
%% Plot Results
figure;
PlotClusterinResult(X, IDX1);
title(['DBSCAN Clustering (\epsilon = ' num2str(epsilon) ', MinPts = ' num2str(MinPts) ')']);
set(gcf,'position',[30 -10 500 500]);
epsilon= 0.25 ;
MinPts= 3 ;
IDX2=DBSCAN(X,epsilon,MinPts);
%% Plot Results
figure;
PlotClusterinResult(X, IDX2);
title(['DBSCAN Clustering (\epsilon = ' num2str(epsilon) ', MinPts = ' num2str(MinPts) ')']);
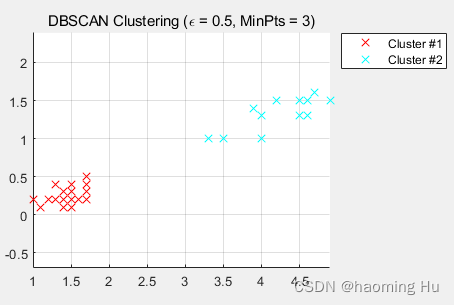
set(gcf,'position',[530 -10 500 500]);epsilon= 0.5 ;
MinPts= 3 ;
IDX3=DBSCAN(X,epsilon,MinPts);
%% Plot Results
figure;
PlotClusterinResult(X, IDX3);
title(['DBSCAN Clustering (\epsilon = ' num2str(epsilon) ', MinPts = ' num2str(MinPts) ')']);
set(gcf,'position',[30 380 500 500]);function [IDX, isnoise]=DBSCAN(X,epsilon,MinPts)C=0;n=size(X,1);IDX=zeros(n,1);D=pdist2(X,X);visited=false(n,1);isnoise=false(n,1);for i=1:nif ~visited(i)visited(i)=true;Neighbors=RegionQuery(i);if numel(Neighbors)<MinPts% X(i,:) is NOISEisnoise(i)=true;elseC=C+1;ExpandCluster(i,Neighbors,C);endendendfunction ExpandCluster(i,Neighbors,C)IDX(i)=C;k = 1;while truej = Neighbors(k);if ~visited(j)visited(j)=true;Neighbors2=RegionQuery(j);if numel(Neighbors2)>=MinPtsNeighbors=[Neighbors Neighbors2]; %#okendendif IDX(j)==0IDX(j)=C;endk = k + 1;if k > numel(Neighbors)break;endendendfunction Neighbors=RegionQuery(i)Neighbors=find(D(i,:)<=epsilon);endend
function PlotClusterinResult(X, IDX)k=max(IDX);Colors=hsv(k);Legends = {};for i=0:kXi=X(IDX==i,:);if i~=0Style = 'x';MarkerSize = 8;Color = Colors(i,:);Legends{end+1} = ['Cluster #' num2str(i)];elseStyle = 'o';MarkerSize = 6;Color = [0 0 0];if ~isempty(Xi)Legends{end+1} = 'Noise';endendif ~isempty(Xi)plot(Xi(:,1),Xi(:,2),Style,'MarkerSize',MarkerSize,'Color',Color);endhold on;endhold off;axis equal;grid on;legend(Legends);legend('Location', 'NorthEastOutside');
end
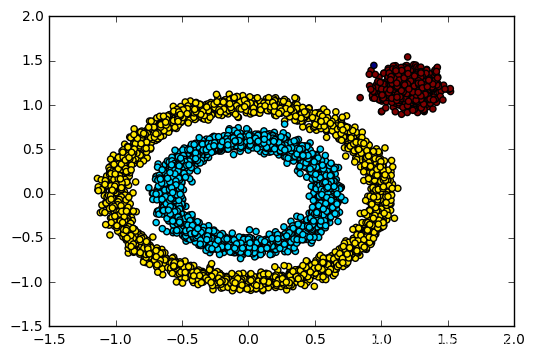
运行结果图:
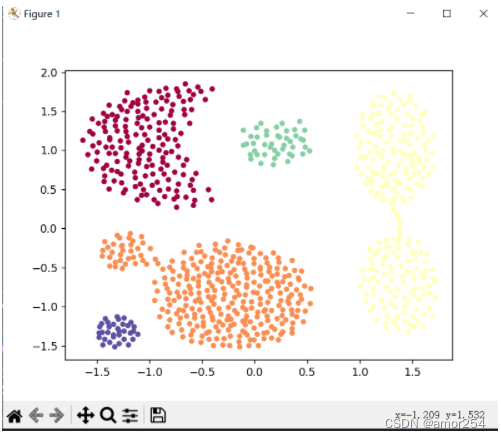
DBSCAN算法对毫米波雷达点云数据进行聚类
(慢慢补全 2023年5月28日19点59分)








![c++ char[]与int之间的类型转换](https://img-blog.csdnimg.cn/0e7a8b1a276e484f8c49405e478d3f70.png#pic_center)