声明：本文修改自《数学建模清风》老师的代码

   DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一个比较有代表性的基于密度的聚类算法。与划分和层次聚类方法不同，它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在噪声的空间数据库中发现任意形状的聚类。 

        作为经典的聚类算法，DBSCAN聚类在数学建模竞赛中用到的概率很大。本文不详细展开讲解DBSCAN的原理，只介绍相关代码的使用步骤。

DBSCAN函数代码：

function [IDX, isnoise]=DBSCAN(X,epsilon,MinPts)C=0;n=size(X,1);IDX=zeros(n,1);  % 初始化全部为0，即全部为噪音点D=pdist2(X,X);visited=false(n,1);isnoise=false(n,1);for i=1:nif ~visited(i)visited(i)=true;Neighbors=RegionQuery(i);if numel(Neighbors)<MinPts% X(i,:) is NOISEisnoise(i)=true;elseC=C+1;ExpandCluster(i,Neighbors,C);endendendfunction ExpandCluster(i,Neighbors,C)IDX(i)=C;k = 1;while truej = Neighbors(k);if ~visited(j)visited(j)=true;Neighbors2=RegionQuery(j);if numel(Neighbors2)>=MinPtsNeighbors=[Neighbors Neighbors2];   %#okendendif IDX(j)==0IDX(j)=C;endk = k + 1;if k > numel(Neighbors)break;endendendfunction Neighbors=RegionQuery(i)Neighbors=find(D(i,:)<=epsilon);endend

绘制聚类图的代码：
 

function PlotClusterinResult(X, IDX)k=max(IDX);Colors=hsv(k);Legends = {};for i=0:kXi=X(IDX==i,:);if i~=0Style = 'x';MarkerSize = 8;Color = Colors(i,:);Legends{end+1} = ['Cluster #' num2str(i)];elseStyle = 'o';MarkerSize = 6;Color = [0 0 0];if ~isempty(Xi)Legends{end+1} = 'Noise';endendif ~isempty(Xi)plot(Xi(:,1),Xi(:,2),Style,'MarkerSize',MarkerSize,'Color',Color);endhold on;endhold off;axis equal;grid on;legend(Legends);legend('Location', 'NorthEastOutside');end

接下来是主函数：

clc;
clear;
close all;load mydata;
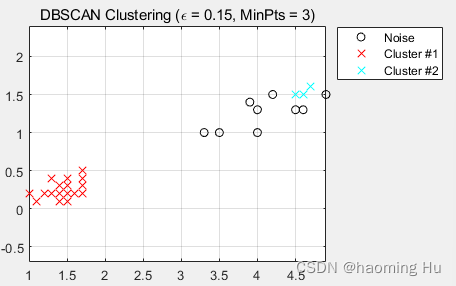
%%注意，此处Data.mat用于导入自己的数据，数据名字要用X，或者在下方改变量名也可以if size(X,2)==2%%如果列数=2才可以运算epsilon=0.5;%%规定聚类半径MinPts=10;%%规定半径内最小数目点%%上面两个参数对聚类的结果很敏感，可以多次修改得出最好的结果IDX=DBSCAN(X,epsilon,MinPts);%%调用DBSCAN函数，输入参数有三个，分别是原始数据，聚类半径，最小数目点%%IDX用于保存每一项数据所属的聚类类别数目PlotClusterinResult(X, IDX);%%画出聚类结果图title(['DBSCAN Clustering (\epsilon = ' num2str(epsilon) ', MinPts = ' num2str(MinPts) ')']);
else disp("请修改数据，DBCASN对二维聚类最佳！")
end

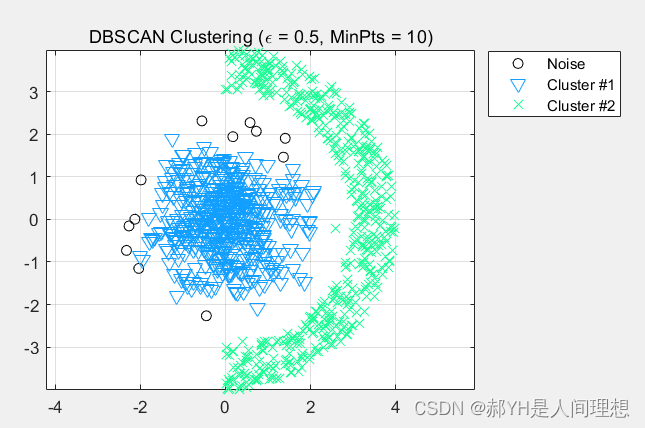
如下是聚类结果：

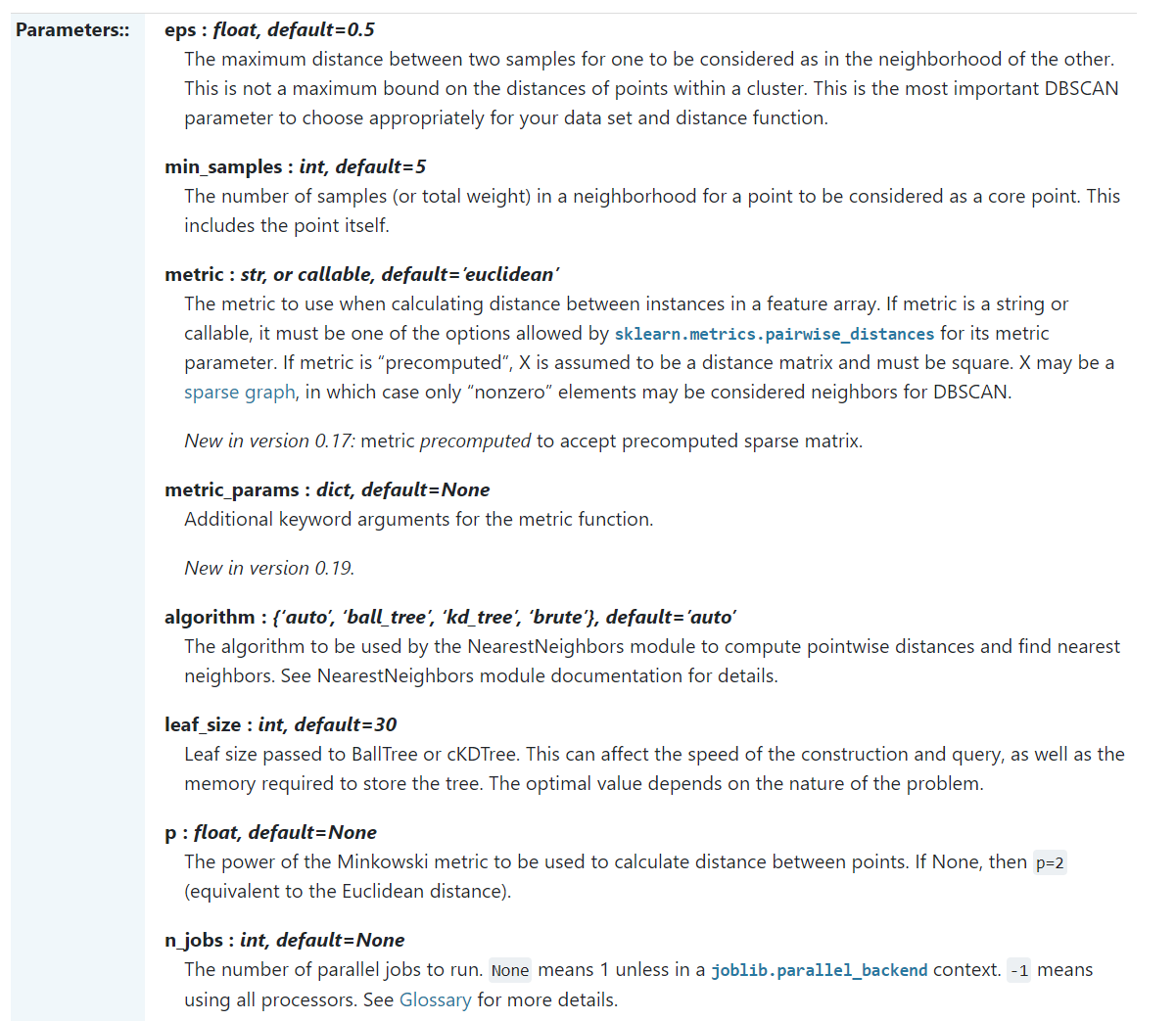
 使用要点：

        前两个函数分别保存为独立的m文件，将其与主函数放置同一文件夹目录之下即可。此外，自己的数据要独立保存为.mat文件，也在同一目录之下。最后直接运行main函数即可。