全网最详细numpy的argmin与argmax解析（一次性理解np.argmin）

article/2025/9/27 12:55:22

本文以np.argmin()进行讲解，np.argmax()与之类似，np.argmin()求最小值对应的索引，np.argmax()求最大值对应的索引

首先看一下官方注释

def argmin(a, axis=None, out=None):"""Returns the indices of the minimum values along an axis.Parameters----------a : array_likeInput array.axis : int, optionalBy default, the index is into the flattened array, otherwisealong the specified axis.out : array, optionalIf provided, the result will be inserted into this array. It shouldbe of the appropriate shape and dtype.

该函数最重要的参数为axis，np.argmin(a, axis=指定值)求的就是a在指定的第axis维度（轴）上的最小值对应的位置索引，若a中在指定轴上有多个最小值，则返回第一个最小值的索引,axis的取值范围就是数据维数的取值范围。其中a可能为list类型，也可能为array类型。

1.若参数a为list类型

np.argmin(a)返回将a中所有元素全部按照原有顺序拉直摊平之后，第一个最小值在其中的位置，举例说明：

import numpy as nplst1=[1,100,56,78,0]
lst2=[[100,0,5],[3,0,7],[5,0,6]]
print("lst列表中的最小值是:")
print(np.min(lst1))
# 仅有一个最小值的情况
print("lst1列表中最小值的索引是：")
print(np.argmin(lst1))
# 有多个最小值的情况
print("lst2列表中最小值的索引是：")
print(np.argmin(lst2))

结果：

2.若参数a为array类型

如果不设置axis的值，则函数默认将a所有数据平铺成一维数组，然后返回其中最小值在平铺序列中的位置，如：

import numpy as np# 一维数组
a=np.array([3, 1, 2, 4, 6, 1])
bb=np.argmin(a)
print('一维数组不设置axis时默认输出结果：')
print(bb)# 二维数组
a=np.array([[1, 5, 5, 2],[9, 6, 2, 8],[3, 7, 9, 1]])
bb=np.argmin(a)
print('二维数组不设置axis时默认输出结果：')
print(bb)# 三维数组
a = np.array([[[1, 5, 5, 2],[9, -6, 2, 8],[-3, 7, -9, 1]],[[-1, 5, -5, 2],[9, 6, 2, 8],[3, 7, 9, 1]]])bb=np.argmin(a)
print('三维数组不设置axis时默认输出结果：')
print(bb)

结果为：

也就是说如果对于array类型的变量a，在应用np.argmin(a)时返回值仅为一个数，返回的是a中所有元素的最小值在平铺a之后的序列中的位置。

(1)一维数组

返回array中数值最小数的下标，默认将输入array视作一维，出现相同的最小，返回第一次出现的

import numpy as np
a=np.array([3, 1, 2, 4, 6, 1])
bb=np.argmin(a)
print(bb)    # bb的值为1

（2）二维数组

二维数组（m*n）假设有m行n列，则每个元素的索引一般写作a[i][j]，其中i=0,1,...m-1，j=0,1,...n-1，i代表元素在第0维上的位置，j代表元素在第1维上的位置。返回值类型为array类型，返回值的长度与第axis维度的各个数据的长度一致。

axis=0，对第0维进行分析：比较j取同一值时，不同的i所指向的元素之间的大小关系，并返回最小值在第axis维度上的索引，返回值是长度为n的一维数组；

axis=1，对第1维进行分析：比较i取同一值时，不同的j所指向的元素之间的大小关系，并返回最小值在第axis维度上的索引，返回值是长度为m的一维数组;

举例说明(m=3,n=4)：

a=np.array([[1, 5, 5, 2],[9, 6, 2, 8],[3, 7, 9, 1]])
bb=np.argmin(a,axis=0)    # 当axis=0时，表示返回列方向上数值最大值下标
cc=np.argmin(a,axis=1)    # 当axis=1时，表示返回行方向上数值最大值下标
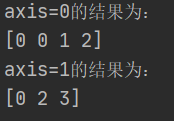
print('axis=0的结果为：')
print(bb) # bb为[0 0 1 2]
print('axis=1的结果为：')
print(cc) # cc为[0 2 3]

结果为：

（3）三维数组

三维数组(m*n*z)假设第0维长度为m，第一维长度为n，第二维长度为z，则每个元素的索引一般写作a[i][j][k]，其中i=0,1,...m-1，j=0,1,...n-1，k=0,1,...z-1,i代表元素在第0维上的位置，j代表元素在第1维上的位置，k代表元素在第2维上的位置。返回值类型为array类型，返回值的类型与第axis维度的各个数据的类型和维数一致。

axis=0表示对第0维进行比较，当j与k取相同值时，不同的i所对应的值的大小关系，返回其中最小值在第0维上的索引，第0维是m个n*z维的二维数组，所以返回数据的类型为n*z维的二维数组；

axis=1表示对第1维进行比较，当i与k取相同值时，不同的j所对应的值的大小关系，返回其中最小值在第1维上的索引，第1维是n个m*z维的二维数组，所以返回数据的类型为m*z维的二维数组；

axis=2表示对第2维进行比较，当i与j取相同值时，不同的k所对应的值的大小关系，返回其中最小值在第2维上的索引，第2维是z个m*n维的二维数组，所以返回数据的类型为m*n维的二维数组；

举例说明（m=2,n=3,z=4):

a = np.array([[[1, 5, 5, 2],[9, -6, 2, 8],[-3, 7, -9, 1]],[[-1, 5, -5, 2],[9, 6, 2, 8],[3, 7, 9, 1]]])bb=np.argmin(a,axis=0)    # 与bb=np.argmin(a,axis=-3)效果相同
cc=np.argmin(a,axis=1)    # 与cc=np.argmin(a,axis=-2)效果相同
dd=np.argmin(a,axis=2)    # 与dd=np.argmin(a,axis=-1)效果相同
print('axis=0的结果为：')
print(bb)
print('axis=1的结果为：')
print(cc)
print('axis=2的结果为：')
print(dd)

结果为：