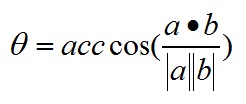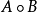内积空间定义
V是 F F F的线性空间的话,对于一种定义的内积运算(运算结果表示为 ( x , y ) , ( x , y ) ∈ F (x,y),(x,y)\in F (x,y),(x,y)∈F),如果能满足四条性质,这个线性空间就是一个内积空间。
(1)共轭对称性: ( x , y ) = ( x , y ) ‾ (x,y) = \overline{(x,y)} (x,y)=(x,y)
(2)可加性: ( x + z , y ) = ( x , y ) + ( z , y ) (x+z,y) = (x,y)+(z,y) (x+z,y)=(x,y)+(z,y)
(3)齐次性: ( k x , y ) = k ( x , y ) (kx,y) = k(x,y) (kx,y)=k(x,y)
(4)正定性: ( x , x ) ≥ 0 (x,x)≥0 (x,x)≥0,当且仅当 x = θ x=\theta x=θ时候取等号
其中实内积空间称为欧几里得空间,复内积空间称为酉空间。酉空间维数=线性空间维数,酉空间的线性子空间仍然是酉空间。
度量矩阵
α 1 , . . . , α n \alpha_1,...,\alpha_n α1,...,αn为内积空间中的基,度量矩阵 A = ( α 1 , . . . , α n ) ′ ⋅ ( α 1 , . . . , α n ) = ( ( α 1 , α 2 ) ( α 1 , α 2 ) . . . ( α 1 , α n ) ( α 2 , α 1 ) . . . . . . ( α 2 , α n ) . . . . . . . . . . . . ( α n , α 1 ) . . . . . . ( α n , α n ) ) A =(\alpha_1,...,\alpha_n)'·(\alpha_1,...,\alpha_n) = \begin{pmatrix} (\alpha_1,\alpha_2) & (\alpha_1,\alpha_2) & ... &(\alpha_1,\alpha_n)\\ (\alpha_2,\alpha_1) & ...&... &(\alpha_2,\alpha_n) \\ ...&...&...&... \\(\alpha_n,\alpha_1) & ... &...& (\alpha_n,\alpha_n)\end{pmatrix} A=(α1,...,αn)′⋅(α1,...,αn)=⎝ ⎛(α1,α2)(α2,α1)...(αn,α1)(α1,α2).....................(α1,αn)(α2,αn)...(αn,αn)⎠ ⎞
(1)度量矩阵是复正定矩阵(复正定包含了厄米特矩阵)
(2)度量矩阵间合同
度量矩阵的意义
∣ G ( α 1 , . . . , α n ) ∣ |G(\alpha_1,...,\alpha_n)| ∣G(α1,...,αn)∣是k维超平行体体积的平方,2维空间中就是一个平行四边形的面积
柯西不等式
证明参考:https://www.bilibili.com/video/BV1Hy4y1b7Pj?p=2
1821年柯西提出柯西不等式
∣ ( α , β ) ∣ ≤ ∣ α ∣ ∣ β ∣ |(\alpha,\beta)|≤|\alpha||\beta| ∣(α,β)∣≤∣α∣∣β∣
1859年布涅科夫斯基提出积分形式
∣ ∫ a b f ( x ) g ( x ) d x ∣ ≤ ( f 2 ( x ) ) ( g 2 ( x ) |\int_a^bf(x)g(x)dx|≤\sqrt{(f^2(x))}\sqrt{(g^2(x)} ∣∫abf(x)g(x)dx∣≤(f2(x))(g2(x)
1888年施瓦茨给出了积分形式的证明,称这个不等式为柯西-布涅科夫斯基-施瓦茨不等式
由柯西不等式有 − 1 ≤ ( α , β ) ∣ α ∣ ∣ β ∣ ≤ 1 -1≤\dfrac{(\alpha,\beta)}{|\alpha||\beta|}≤1 −1≤∣α∣∣β∣(α,β)≤1,可以定义向量夹角
< α , β > = a r c c o s ( α , β ) ∣ α ∣ ∣ β ∣ <\alpha,\beta>=arccos\dfrac{(\alpha,\beta)}{|\alpha||\beta|} <α,β>=arccos∣α∣∣β∣(α,β)
向量夹角取值 0 ≤ < α , β > ≤ π 0≤ <\alpha,\beta> ≤π 0≤<α,β>≤π
在欧氏空间中可以得到三角不等式、勾股定理、余弦定理
三角不等式:
∣ α + β ∣ ≤ ∣ α ∣ + ∣ β ∣ |\alpha+\beta|≤|\alpha|+|\beta| ∣α+β∣≤∣α∣+∣β∣
勾股定理:
∣ α + β ∣ 2 = ∣ α ∣ 2 + ∣ β ∣ 2 |\alpha+\beta|^2=|\alpha|^2+|\beta|^2 ∣α+β∣2=∣α∣2+∣β∣2
余弦定理:
∣ γ ∣ 2 = ∣ α ∣ 2 + ∣ β ∣ 2 − 2 ∣ α ∣ ∣ β ∣ c o s < α , β > |\gamma|^2=|\alpha|^2+|\beta|^2-2|\alpha||\beta|cos<\alpha,\beta> ∣γ∣2=∣α∣2+∣β∣2−2∣α∣∣β∣cos<α,β>