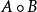以下是在向量中的运算,即类似,而不是矩阵中的运算!
内积(inner product, scalar product,dot product)
根据翻译,内积又叫标量积、点积,还叫数量积。是指接受在实数R上的两个向量并返回一个实数值标量的二元运算。它是欧几里得空间的标准内积。
两个向量和
的点积定义为:
使用矩阵乘法并把(纵列)向量当作n×1 矩阵,点积还可以写为:
其中,指示矩阵a的转置。注:有的同学觉得是
,其实都没有错,到底是a的转置矩阵乘b,还是a乘b的转置取决于向量的矩阵表示方法,即一个n维向量,是用n*1的矩阵表示还是用1*n的矩阵表示。一般情况下,线性代数中,向量(vector)用列(column)而不是行(row)来表示,即N*1的矩阵表示一个N维向量。所以用a的转置矩阵乘b。疑问主要是因为对“向量”和“矩阵表示”没有区分。前面的两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]并不代表他是1*n的矩阵表示。
点积有两种定义方式:代数方式和几何方式。通过在欧氏空间中引入笛卡尔坐标系,向量之间的点积既可以由向量坐标的代数运算得出,也可以通过引入两个向量的长度和角度等几何概念来求解。
代数定义
设二维空间内有两个向量和
,定义它们的数量积(又叫内积、点积)为以下实数:
几何定义
设二维空间内有两个向量和
,
和
表示向量a和b的大小,它们的夹角为
,则内积定义为以下实数:
该定义只对二维和三维空间有效。 这个运算可以简单地理解为:在点积运算中,第一个向量投影到第二个向量上(这里,向量的顺序是不重要的,点积运算是可交换的),然后通过除以它们的标量长度来“标准化”。这样,这个分数一定是小于等于1的,可以简单地转化成一个角度值。
```
x = numpy.array([1, 2])
y = numpy.array([10, 20])
print("Array inner:")
print(numpy.inner(x, y))
''' Output:
Array inner:
50
'''
x = numpy.mat([[1, 2], [3, 4]])
y = numpy.mat([10, 20])
print("Matrix inner:")
print(numpy.inner(x, y))
''' Output:
Matrix inner:
[[ 50][110]]
'''
```外积(Out product、Cross product、Vector product)
根据翻译,又称向量积、叉乘。数学中称向量积、外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。其应用也十分广泛,通常应用于物理学光学和计算机图形学中。
对三维空间中的两个向量和
作叉积
,返回一个向量
,
垂直于
和
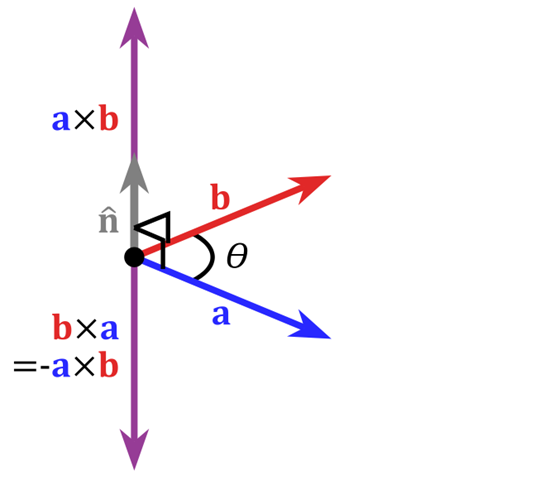
。在三维几何中,向量a和向量b的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于a和b向量构成的平面。在3D图像学中,叉乘的概念非常有用,可以通过两个向量的叉乘,生成第三个垂直于a,b的法向量,从而构建X、Y、Z坐标系。如下图所示:
在二维空间中,叉乘还有另外一个几何意义就是:等于由向量a和向量b构成的平行四边形的面积。
代数定义
几何定义
向量积可以被定义为:
模长:(在这里θ表示两向量之间的夹角(共起点的前提下)(0°≤θ≤180°),它位于这两个矢量所定义的平面上。)
方向:a向量与b向量的向量积的方向与这两个向量所在平面垂直,且遵守右手定则。(一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的:若坐标系是满足右手定则的,当右手的四指从a以不超过180度的转角转向b时,竖起的大拇指指向是c的方向。)
也可以这样定义(等效):
在二维向量中,向量积|c|=|a×b|=|a||b|sin<a,b>,即c的长度在数值上等于以a,b,夹角为θ组成的平行四边形的面积。而c的方向垂直于a与b所决定的平面,c的指向按右手定则从a转向b来确定。*运算结果c是一个伪向量。这是因为在不同的坐标系中c可能不同。
区别
| 名称 | 标积/内积/数量积/点积 | 矢积/外积/向量积/叉积 |
| 运算式(a,b和c粗体字,表示向量) | a·b=|a||b|·cosθ | a×b=c,其中|c|=|a||b|·sinθ,c的方向遵守右手定则 |
| 几何意义 | 向量a在向量b方向上的投影与向量b的模的乘积 | c是垂直a、b所在平面,且以|b|·sinθ为高、|a|为底的平行四边形的面积 |
| 运算结果的区别 | 标量(常用于物理)/数量(常用于数学) | 矢量(常用于物理)/向量(常用于数学) |