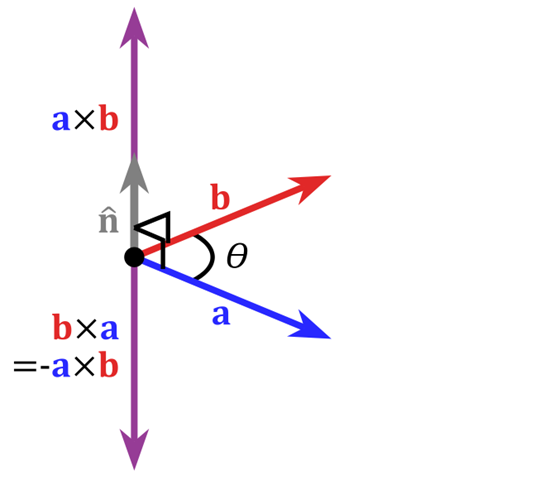
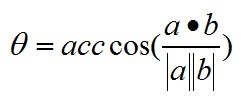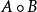下面是定义:

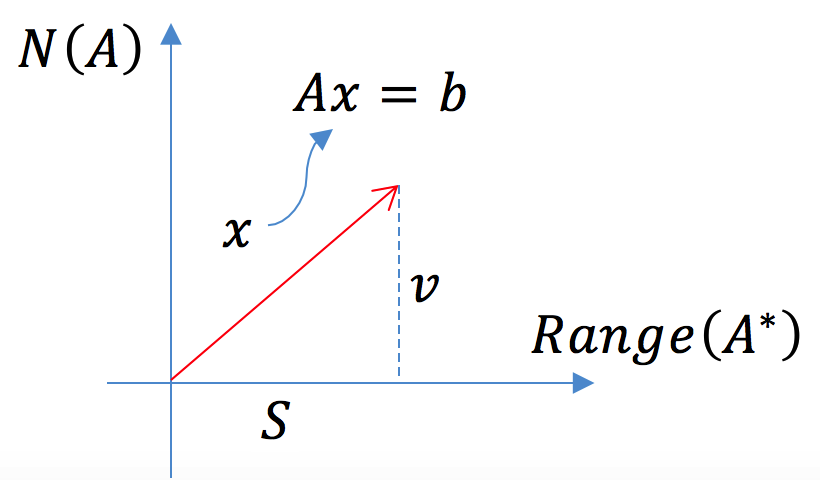
Ax的结果会让我们想起之前的线性系统和多元一次方程组

也就是说,向量x在经过矩阵A的变换后,得到了向量B
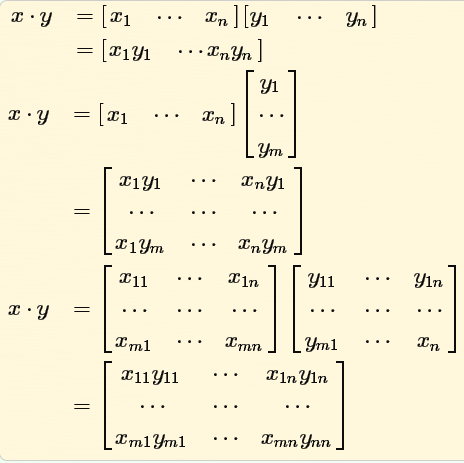
下面以两种观点来看矩阵与向量的乘积。
- row aspect

矩阵的第n行与向量做内积,然后将结果放在第n行
2.column aspect

将矩阵的每一列看做一个向量,乘积的结果是一个线性组合,其线性的系数就是向量x的每个分量
举个例子

上图左边的那个方程组,对两个x变量进行赋值后,可以看做将这两个变量放入一个线性系统的输入端,然后观察输出
1.行角度
我觉得行的角度没有什么几何意义,至少从这个图来讲是这样的。(不太喜欢这个解释)
2.列角度
从图中可以看到,就是对原线性系统中的两个列向量进行了伸缩之后再相加得到的结果!
相乘的时候维度也要注意

无论是行的角度还是列的角度,上图的x与A都是不能相乘的,与A ′ \prime ′就可以
矩阵与向量相乘的性质:

注意一下第五个,这里的零向量在相乘之前是n维的,相乘之后是m维的。
最后这个比较有意思

只看问题描述的话,很有可能觉得是错的,
我们可以这么想,对于w向量,每次取标准向量这样得到的就是该矩阵的特定的那一列,如果每列都相同,那自然两个矩阵也就一样了。
若有两个黑盒子,是线性系统的,有人让你看看这两个线性系统是不是完全一样的,我们就不必把所有的输入都试一下观察输出,只需试一下不同的标准向量就ok啦