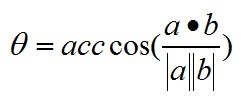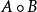1.向量
向量是一个既有大小又有方向的量,在物理学中又把向量叫作矢量。(与之对应的叫标量,只有大小的量)
一般用一个有向线段来表示向量,如下图:

向量几何表示时,在字母上面加上箭头,如:
向量代数表示时,一般是小写的黑体字母,如:a、b、c等,但是手写时无法明确体现黑体,所以也常在字母上加箭头,如:
为了能将向量像数字一样进行运算,在数学上我们还必须把向量放在某一个坐标系里:如果把空间中所有的向量的尾部都拉倒坐标原点,这样n维点空间就可以与n维向量空间建立一一对应关系。n维点空间中的点(0,0,0...)取作原点,那么每一个点都可以让一个向量和它对应,这个向量就是从坐标原点出发到这个点为止的向量。
确定完坐标系,向量与点就是一一对应的,点使用坐标的有序数组来表示,那么向量也可以用坐标的有序数组表示。通过向量的有序数组来对向量进行运算。例如:二维坐标系中,=(4,5),有序数组(4,5)就是向量
2.向量的内积定义
向量的内积也叫数量积、标积、点积。
内积的定义有两个,如下:
(其中
表示向量a的长度,有的也用
表示长度)
向量a和b的长度之积再乘以它们之间的夹角的余弦。
向量a和b的坐标分量分别对应乘积的和。
刚接触到向量的内积定义时,纳闷为啥会有两种定义,从定义上可以看出两种定义的结果都是一个数值,那这两种定义所给定的不同计算方式最终的结果值应该是一致的,如何验证?
3.向量内积的几何解释
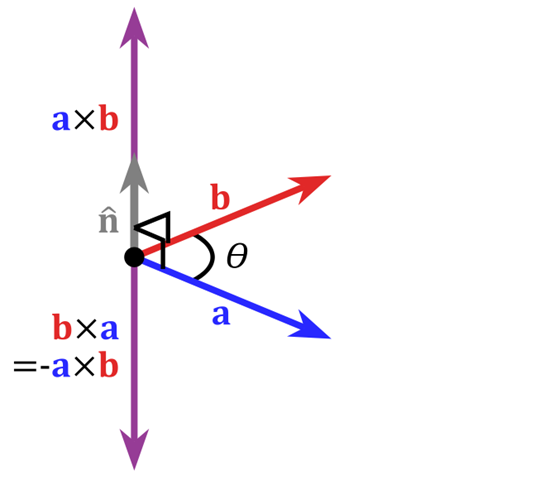
以三维空间为例,取任意的两个向量a和b,将两个向量的尾部重合与原点,,以向量a和b的相交组成的平面作为x0y所在的平面,并其中任意的一个向量作为x轴,下图中以向量a作为x轴,如图

那么向量a在y轴和z轴上的分量都是0,即
,其中
就是向量b在x轴上的分量,为
从几何角度上验证了向量内积两种定义的一致性。
4.向量内积的物理解释

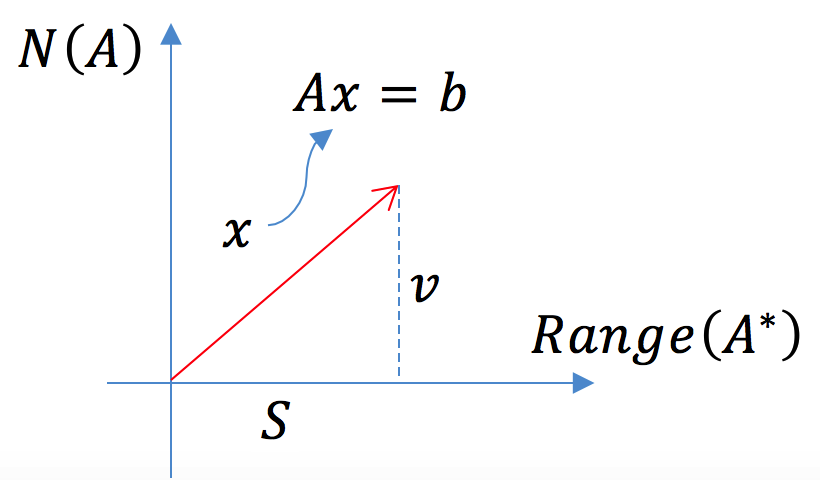
假设在一个斜坡上,力F沿着斜坡将重物移动做功,位移为S,如上图,此时整体做功为

从另一个角度,我们把力F沿着位移S方向和垂直S的方向进行分解,做功为
两者做功是一致的,由此,我们从物理角度上验证了向量内积两种定义的一致性。
学习书籍:
《线性代数的几何意义》任广千
《3D数学基础——图形和游戏开发(第2版)》Fletcher Dunn