本文内容基于《算法笔记》和官方配套练题网站“晴问算法”,是我作为小白的学习记录,如有错误还请体谅,可以留下您的宝贵意见,不胜感激。
文章目录
- 前言
- 一、动态规划概述
- 二、算法设计
- 1.上楼||
- 2.最大连续子序列和
- 动态规划
- 分治
- 3.最大连续子序列和的最优方案
- 三、备注
前言
动态规划(Dynamic Programming,DP)是一种用来解决一类最优化问题的算法思想。简单来说,动态规划将一个复杂的问题分解成若干个子问题,通过综合子问题的最优解来得到原问题的最优解。需要注意的是,动态规划会将每个求解过的子向题的解记录下来,这样当下一次碰到同样的子问题时,就可以直接使用之前记录的结果,而不是重复计算。注意:虽然动态规划采用这种方式来提高计算效率,但不能说这种做法就是动态规划的核心。一般可以使用递归或者递推的写法来实现动态规划,其中递归写法在此处又称作记忆化搜索,递推写法是自底向上,递归写法是自顶向下(和面向过程和面向对象相似但不完全一样)。
一、动态规划概述
动态规划粗俗点可以说是对分治算法的优化,一切可以用动态规划解决的问题都可以用分治解决,其核心是状态转移方程。动态规划是解决最优解的算法,一个问题必须拥有重叠子问题和最优子结构,才能用动态规划去解决。重叠子问题很好理解,在递归中又被称为记忆化搜索;最优子结构指原问题的最优解可以由其子问题的最优解构造出来,并不一定是满足分治法那样到达递归边界即为解,而是需要将子问题的最优解记录下来,通过某种关系用子问题的最优解“构造”出原问题的最优解,至于怎么构造,就取决于个人理解了。
所以,动态规划的解题步骤如下:
1.通过原问题分析最优子结构,即将原问题分解为子问题,分析子问题中存在的重叠子问题;
2.设置状态dp记录子问题的最优解,设计状态转移方程描述原问题与子问题之间的递推关系(当然可以用分治法来分析原问题并采用递归)。
3.求解dp,并通过dp来构造原问题的最优解。
二、算法设计
1.上楼||
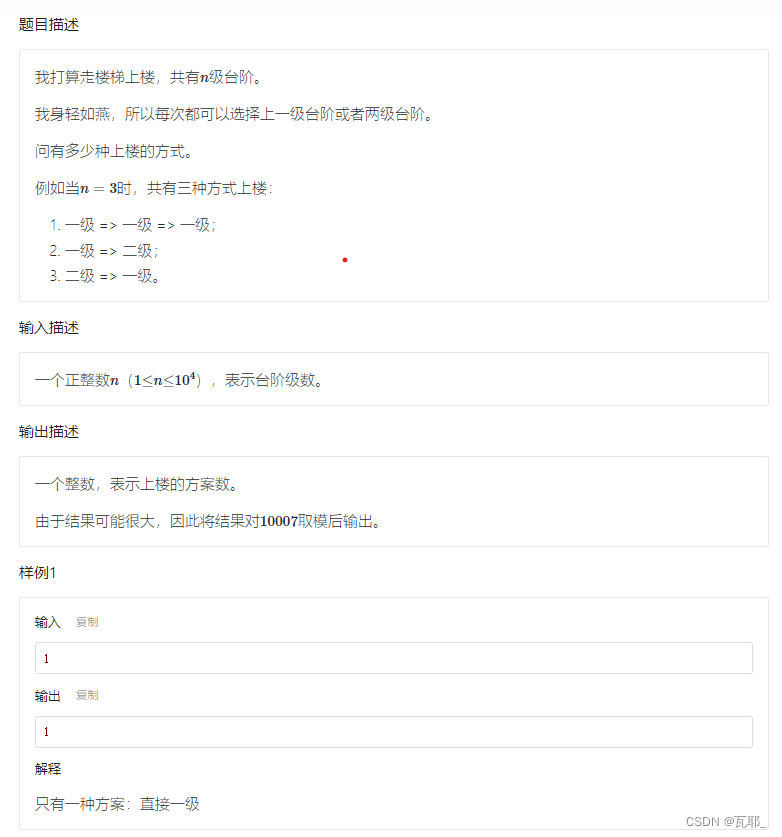
首先先把这道题的描述转化为最优解问题,即求最大上楼策略。
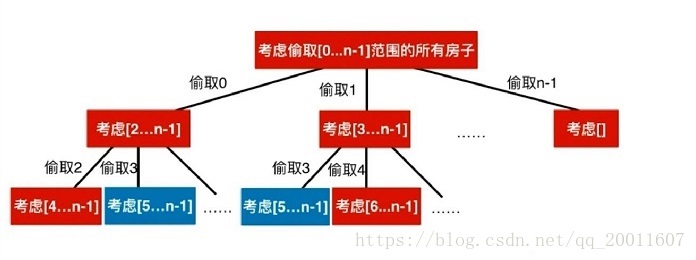
1.问题分解:找到题中的子问题,这很容易,就是走一级台阶或者两级台阶,所以可以画出问题分解图如下:
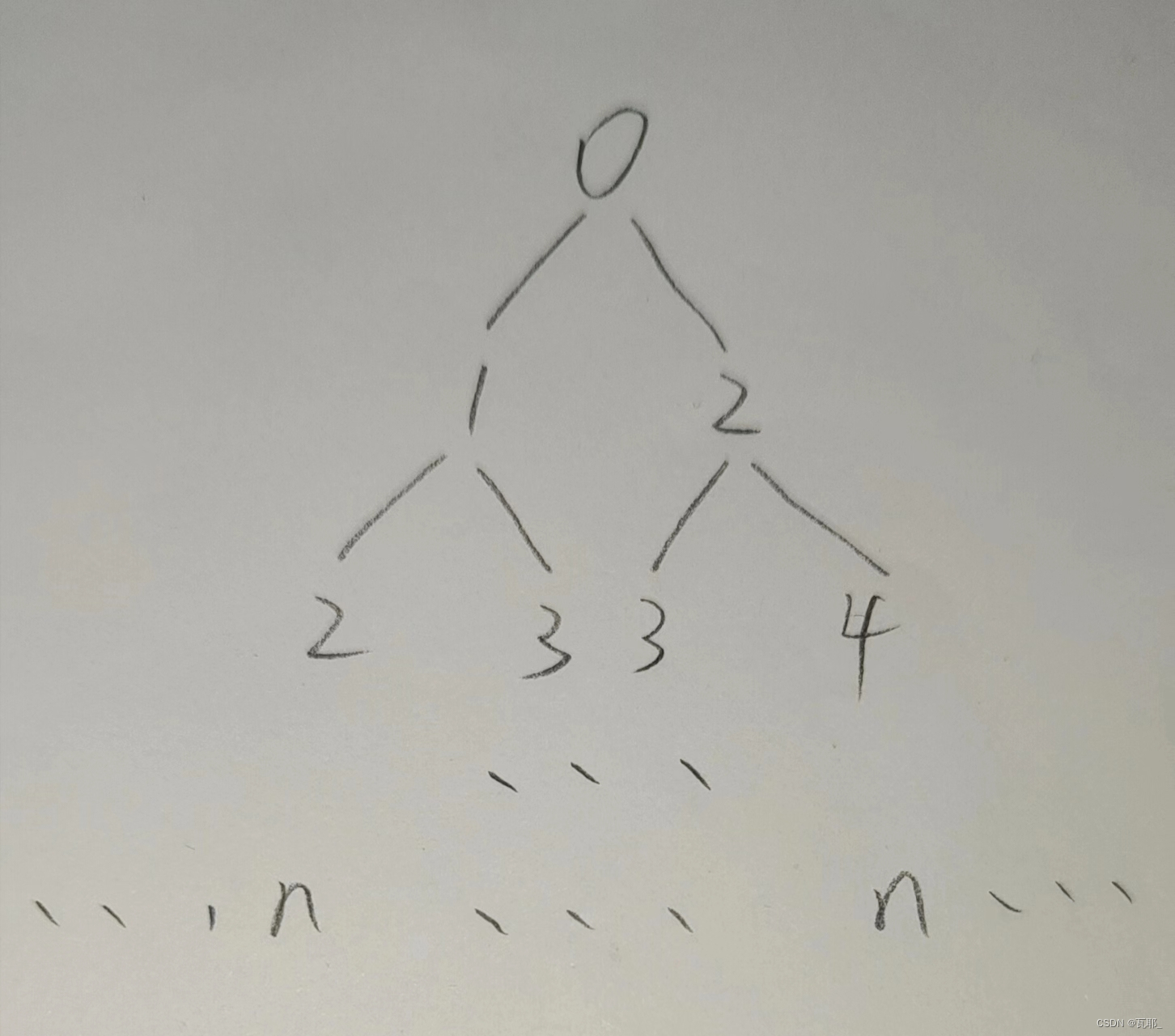
当然也可以从n向下画;
2.设计状态和状态转移方程:dp[i]记录走到某个台阶时继续向下走的最大方案数,所以可以设计状态转移方程为:dp[i] = dp[i + 1] + dp[i + 2];
3.从底层开始循环,通过状态转移方程扩散到整个数组,dp[0]即为求解。
注:递归实现更简单,这里就不赘述了。
完整代码如下:
#include<cstdio>
const int MAXN = 10000;
int dp[MAXN] = {};
int main(){int n;scanf("%d", &n);dp[n] = 0;dp[n - 1] = 1;dp[n - 2] = 2;for(int i = n - 3; i >= 0; i--)dp[i] = (dp[i + 1] + dp[i + 2]) % 10007;printf("%d", dp[0]);
}
2.最大连续子序列和
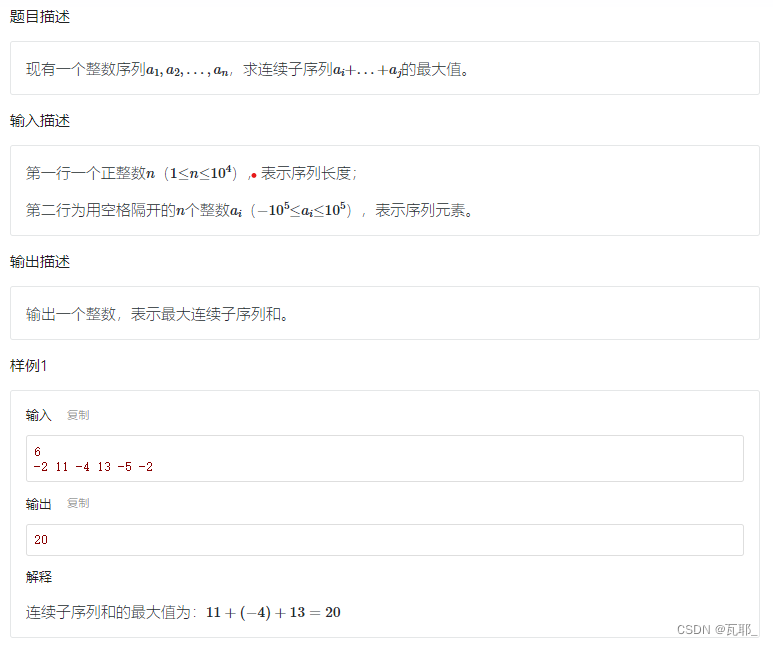
这道题有两种解法,分治法和动态规划,这里先分析动态规划法。
动态规划
1.问题分解:将原问题这样分解:求a1····an-1序列的连续子序列最大值,并判断A[i]的状态是加入序列或者以A[i]为子序列首元素;求a1···an-2······
2.设计状态和状态转移方程:dp[i]为以A[i]为结尾连续序列的最大和,所以可以设计状态转移方程为:dp[i] = max(A[i] , dp[i - 1] + A[i]);通过这个状态转移方程可以认识到并不需要枚举左端点,因为每一个子问题的最优解都可以借由前一个子问题的最优解推导出来;
3.从底层开始循环,通过状态转移方程扩散到整个数组,dp[i]中的最大值就是原问题的最优解,注意不是dp[n]。
完整代码如下:
#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN = 10000;
int A[MAXN] = {};
int dp[MAXN] = {};int main(){int n;scanf("%d", &n);for(int i = 0; i <= n - 1; i++) scanf("%d", A + i);dp[0] = A[0];int MAX = -10e5;for(int i = 1; i <= n - 1; i++) {dp[i] = max(A[i] , dp[i - 1] + A[i]);if(dp[i] > MAX) MAX = dp[i];}printf("%d", MAX);
}
分治
1.问题分解:
如果将所给的序列A[1…n]分为长度相等的两段A[1…n/2]和A[n/2+1…n],分别求出这两段的最大字段和,则A[1…n]的最大子段和有3种情形:
(1)A[1…n]的最大子段和与A[1…n/2]的最大子段和相同;
(2)A[1…n]的最大子段和与A[n/2+1…n]的最大子段和相同;
(3)A[1…n]的最大子段和是在A[1…n/2]和A[n/2+1…n]上的两个片段,即在A[1…n]的中间位置;
2.解决:
(1)和(2)采用递归解决,对(3)可以从n/2和n/2+1为起点,分别在两个片段中求出最大子序列和,然后求和即为A[1…n]的最大子段和;
3.合并:
比较在分解阶段的3种情况下的最大子段和,取三者中的较大者为原问题的解。
完整代码就先不放了(没时间写了···),对于这本书,最重要的是第一种方法,因为之后的例题都是采用这种思路的。
3.最大连续子序列和的最优方案

这道题在上一道题的基础上,需要记录到达每一个以A[i]为结尾的最大连续子序列的首元素和尾元素,所以可以开一个结构体存储首尾元素位置,随着动态规划的求解不断记录首尾元素,最后将第一个最大子序列和对应的以A[i]为结尾的首尾元素。其中,结构体的记录有三种情况:
if(A[i] > dp[i - 1] + A[i]) Node[i] = {i , i};
if(A[i] < dp[i - 1] + A[i]) Node[i] = {Node[i - 1].i , i};
if(A[i] == dp[i - 1] + A[i]) Node[i] = {Node[i - 1].i , i};
前两个分别代表以A[i]为新的子序列首尾元素和将A[i]加入上一个序列的情况。但是在首尾元素的选择上还存在第三种情况,即A[i] == dp[i - 1] + A[i],这个情况在计算最大和时并不需要考虑在内,但现在是要求具体的首尾元素位置,并且在存在多解的情况下总是选择首元素下标最小的解(在判断最大值时就已经是尾元素下标最小的情况了),那么当碰到A[i] == dp[i - 1] + A[i]时,意味着A[i]和dp[i - 1] + A[i]都可以满足情况,这时为了满足首元素位置最小的情况,就将A[i]加入前一序列,而不是以A[i]为新序列的首元素。
完整代码如下:
#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN = 10000;
int A[MAXN] = {};
int dp[MAXN] = {};
struct node{int i , j;
}Node[MAXN]; //记录当前序列的首位坐标 int main(){int n;scanf("%d", &n);for(int i = 0; i <= n - 1; i++) scanf("%d", A + i);dp[0] = A[0];Node[0] = {0 , 0};int MAX = -10e5;int MAXI = 0;for(int i = 1; i <= n - 1; i++) {dp[i] = max(A[i] , dp[i - 1] + A[i]);if(dp[i] > MAX) { //记录的就是最小的尾元素下标MAX = dp[i];MAXI = i; //记录结尾 }if(A[i] > dp[i - 1] + A[i]) Node[i] = {i , i}; //以A[i]为首尾if(A[i] < dp[i - 1] + A[i]) Node[i] = {Node[i - 1].i , i}; //将A[i]加入上一个序列 if(A[i] == dp[i - 1] + A[i]) Node[i] = {Node[i - 1].i , i}; //总是将A[i]加入上一个序列 }printf("%d %d %d", MAX , Node[MAXI].i + 1 , Node[MAXI].j + 1);
}
三、备注
1.注意体会重叠子问题和最优子结构在递归和递推中的体现;
2.原问题的最优解是由子问题的最优解构建出来的,这一点还是区别于分治法的将问题缩小到最小子问题解决的思路;
3.分治与动态规划的区别(摘自算法笔记):分治和动态规划都是将问题分解为子问题,然后合并子问题的解得原问题的解。但是不同的是,分治法分解出的子问题是不重叠的,因此分治法解决的问题不拥有重叠于间题,而动态规划解决的问题拥有重叠子问题。例如,归并样序和快速排序是分别处理左序列和右序列,然后将左右序列的结果合并,过程中不出现重叠子问题,因此它们使用的都是分治法。另外,分治决的问题不一定是最优化问愿,而动态规划解决的问题一定是最优化问题。
4.贪心与动态规划的区别(摘自算法笔记):贪心和动态规划都要求原问题必须拥有最优子结构。二者的区别在于,贪心法采用的计算方式类似于上面介绍的“自顶向下”,但是并不等待子问题求解完毕后再选择使用哪一个,而是通过一种策略直接选择一个子问题去求解,没被选择的子问题就不去求解了,直接抛弃。也就是说,它总是只在上一步选择的基础上继续选择,因此整个过程以一种单链的流水方式进行,显然这种所谓“最优选择”的正确性需要用归纳法证明。例如对数塔问题而言,贪心法从最上层开始,每次选择左下和右下两个数字中较大的一个,一直到最底层得到最后结果,显然这不一定可以得到最优解。而动态规划不管是采用自底向上还是自项向下的计算方式,都是从边界开始向上得到目标问题的解。也就是说,它总是会考虑所有子问题,并选择继承能得到最优结果的那个,对暂时没被继承的子问题,由于重叠子问题的存在,后期可能会再次考虑它们,因此还有机会成为全局最优的一部分,不需要放弃。所以贪心是一种壮士断腕的决策,只要进行了选择,就不后悔:动态规划则要看哪个选择笑到了最后,暂时的领先说明不了什么。