**动态规划(DP)
一.基本概念
动态规划(英语:Dynamic programming,简称DP)是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
它针对满足特定条件的一类问题,对各维度进行分阶段、有顺序、无重复、决策性的遍历求解。
动态规划算法将原问题视作若干个重叠子问题的逐层递进,每个子问题的求解过程都构成一个阶段。
在完成前一个阶段的计算之后,动态规划才会进入到下一个阶段的计算。
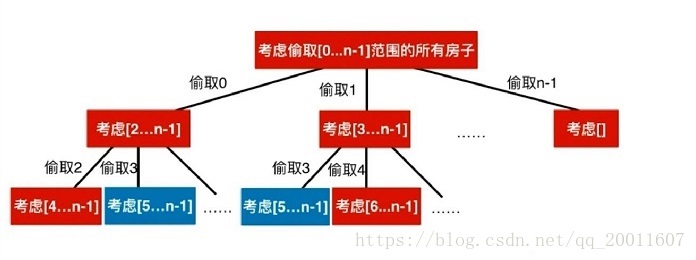
子问题重叠性质:子问题重叠性质是指在用递归算法自顶向下对问题进行求解时,每次产生的子问题并不总是新问题,有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只计算一次,然后将其计算结果保存在一个表格中,当再次需要计算已经计算过的子问题时,只是在表格中简单地查看一下结果,从而获得较高的效率。
为了保证这些计算能按顺序、不重复地进行,动态规划要求已经求解地子问题不受后续状态的影响。
这个条件也被称为无后效性
无后效性:即子问题的解一旦确定,就不再改变,不受在这之后、包含它的更大的问题的求解决策影响。
换句话说,动态规划对状态空间的遍历构成一张有向无环图,遍历顺序就是一个拓扑序。
节点对应问题中的状态,边对应问题的转移,转移的选取就是动态规划中的决策。
在很多情况下,动态规划用于求解最优化问题。
此时,下一阶段的最优解应该能由前面各状态的各阶段子问题的最优解导出。
这个条件被称为最优子结构性质。
最优子结构:问题的最优解由相关子问题的最优解组合而成,而这些子问题可以独立求解。
状态、阶段、决策是动态规划的三要素,
而子问题重叠性质、无后效性、最优子结构性质是求解的三个基本条件。
一般求解过程:
要去刻画最优解的结构特征(确定三要素,检查三个基本条件);
尝试递归地定义最优解的值(求出状态转移方程);
计算最优解(确定转移顺序);
利用计算出的信息构造一个最优解。
二.记忆化搜索
想体验把暴搜改改就是正解的快感吗?想体验状压 dp 看似状态多到爆炸实际一跑却嗷嗷快(实际有效的状态数很少)的荣耀吗?记忆化搜索,符合您的需求!买不到吃亏买不到上当!只要 998 , 记忆化搜索带回家!记忆化搜索,记忆化搜索,再说一遍,记忆化搜索!
首先,你的搜索需要满足一些前提:
不依赖任何 外部变量
答案以返回值的形式存在,而不能以参数的形式存在(就是不能将 定义成 dfs(int pos,int nowans) , 这里面的 nowans 不符合要求)。
对于相同一组参数, 返回值总是相同的(如果你满足了前两条这一条一般也满足,随机化除外)。
此时我们就可以建立一个记忆数组,将一组参数第一次传入时的返回值记录下来,之后再次传入时就可以直接返回中的值。
简单举个例子,数字三角形**
int dfs(int i, int j)
{if (i > n) return 0; //如果下越界,则返回0,不会贡献答案if (j > i) return -inf; //如果右越界,则返回负无穷,就不可能被选择if (m[i][j] < inf) return m[i][j];return m[i][j] = max(dfs(i + 1, j), dfs(i + 1, j + 1)) + mp[i][j];
}
其实说白了,记忆化搜索就是dp
根据记忆化搜索的参数可以直接得到dp的状态,反之亦然
根据记忆化搜索的递归关系可以写出状态转移方程,这个方程可以直接写出循环式的dp,只不过是反的(想想为什么?),反之亦然
大部分记忆化搜索时空复杂度与 不加优化的 dp 完全相同
最重要的一点:二者思想类似!! 核心思想均为:利用对于相同参数答案相同的特性,对于相同的参数(循环式的dp体现为数组下标),记录其答案,免去重复计算,从而起到优化时间复杂度的作用。这,便是二者的精髓。
优点
记忆化搜索可以避免搜到无用状态, 特别是在有状态压缩时
不需要注意转移顺序
边界情况非常好处理, 且能有效防止数组访问越界
写起来简单易懂
有些 dp(如区间 dp)用记忆化搜索写很简单但正常 dp 很难
记忆化搜索天生携带搜索天赋,可以使用技能”剪枝”!
缺点
致命伤: 不能滚动数组!
有些优化比较难加
由于递归, 有时效率较低但不至于 TLE
老样子,举几个例题你就明白了:
let one:

dp:
#include <iostream>
using namespace std;
int n,a[30][30],f[30][30];
int pmax(int a,int b)
{if(a>b)return a;return b;
}
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){scanf("%d",&a[i][j]);}}a[n/2][n/2]+=100000000;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j];//这是公式,学了dp的应该知道}}int ans=-1;for(int i=1;i<=n;i++){ans=pmax(ans,f[n][i]);}printf("%d",ans-100000000);return 0;
}再来个例子:

爆搜(暴力搜索):
#include<iostream>
using namespace std;
int a[1100],f[1100],s[1100];
int main()
{int ans=0,n=1;while(cin>>a[n]){n++;}for(int i=1;i<n;i++){int falg=1,t=0;for(int j=i-1;j>=1;j--){if(a[j]>=a[i]){if(f[j]>t) {t=f[j];}falg=0;}}if(falg) f[i]=1;else f[i]=t+1;ans=max(ans,f[i]);}cout<<ans<<endl;int m=0,p;for(int i=1;i<=n;i++){int x=9999999,flag=1;for(int k=1;k<=m;k++){if(s[k]>=a[i]){if(s[k]<=x) {x=s[k];p=k;}flag=0;}}if(flag) {m++;s[m]=a[i];}else {s[p]=a[i];}} cout<<m<<endl;return 0;
}
写了这么多,还是请求各位大来给我一个赞