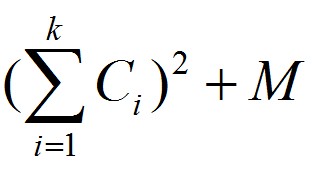动态规划（DP）小结

article/2025/9/29 9:13:04

目录

动规解题的一般思路

能用动规解决的问题的特点

动归的常用形式

例题

例题一：最长公共子序列

例题二：最大子段和

例题三：最长上升子序列(最长单调递增)

 例题四：数字三角形

例题五 0-1背包问题

应用题

应用一：合唱队形（最长递增、递减序列）

应用二：数塔问题（数字三角形）

动规解题的一般思路


1.将原问题分解为子问题

  • 把原问题分解为若千个子问题，子问题和原问题形式相同或类似，只不过规模变小了。子问题都解决，原问题即解决(数字三角形例)
  • 子问题的解一旦求出就会被保存，所以每个子问题只需求解一次。

2.确定状态

  • 将和子问题相关的各个变量的一组取值，称之为一个“状态”。一个“状态”对应于一个或多个子问题,所谓某个“状态”下的“值”就是这个“状态”所对应的子问题的解。
  • 所有“状态”的集合，构成问题的“状态空间”，“状态空间”的大小，与用动态规划解决问题的时间复杂度直接相关。
  • 整个问题的时间复杂度是状态数目乘以计算每个状态所需时间。

在数字三角形的例子里，一共有N*(N+1)/2个数字，所以这个问题的状态空间里一共就有N* (N+1)/2个状态。数字三角形中每个“状态”只需要经过一次，且在每个状态上作计算所花的时间都是和N无关的常数。

用动态规划解题，经常碰到的情况是，K个整型变量能构成一个状态(如数字三角形中的行号和列号这两个变量构成“状态”)。如果这K个整型变量的取值范围分别是N1, N2, ..... Nk，那么我们就可以用一个K维的数组array[N1] [N2.]....Nk]来存储各个状态的“值”。这个值”未必就是一个整数或浮点数，可能是需要一个结构才能表示的，那么array就可以是一个结构数组。一个“状态”下的‘‘值’通常会是一个或多个子问题的解。

3.确定一些初始状态(边界状态)的值
以“数字三角形”为例，初始状态就是底边数字，值就是底边数字值。

4.确定状态转移方程
定义出什么是“状态”，以及在该“状态”下的“值”后，就要找出不同的状态之间如何迁移，即如何从一个或多个“值”已知的“状态”，求出另一个“状态”的“值”(“人人为我”递推型)。状态的迁移可以用递推公式表示，此递推公式也可被称作“状态转移方程”。
 

能用动规解决的问题的特点

  • 问题具有最优子结构性质。即问题的子问题的解也是最优的。
  • 无后效性。当前的若干个状态值一旦确定，则此后过程的演变就只和这若干个状态的值有关，和之前是采取哪种手段或经过哪条路径演变到当前的这若干个状态，没有关系。

动归的常用形式

  • 递归型
    • 优点：直观，容易编写
    • 缺点：可能会因递归层数太深导致爆栈，函数调用带来额外时间开销。无法使用滚动数组节省空间。总体来说，比递推型慢。
  • 递推型
    • 效率高，有可能使用滚动数组节省空间

例题

例题一：最长公共子序列

1.描述

给出两个字符串，求最长的公共子序列的长度。

公共子序列：子序列中的每个字符都能在两个原串中找到，而且每个字符的先后顺序和原串中的先后顺序一致。

 2.样例输入：

abcfbc abfcab
programming
contest
abcdmnp

3.样例输出：

4

2

0

（1）找出子问题

输入两个串s1 ,s2,
设MaxLen(i,j)表示：s1的左边i个字符形成的子串，与s2左边的j个字符形成的子串的最长公共子序列的长度(i,j从0开始)

（2）确定状态
MaxLen(i,j)就是本题的“状态”
假定len1 = strlen(s1),len2 = strlen(s2)那么题目就是要求MaxLen(len1,len2)

（3）状态转移方程

MaxLen(n,0) =0 ( n=0...len1)
MaxLen(0,n) =0 ( n=0...len2)
通过观察可以得到递推公式：

if(s1[i-1] == s2[j-1] )//s1的最左边字符是s1[0]MaxLen(i,j) = MaxLen(i-1,j-1) + 1;
elseMaxLen(i,j) = Max(MaxLen(i,j-1),MaxLen(i-1,j));
  • 当s1[i]＝s2[j]时，找出s1[i-1]和s2[j-1]的最长公共子序列，然后在其尾部加上s1[i]（＝s2[j]）即可得s1和s2一个最长公共子序列。
  • 当s1[i]≠s2[j]时，必须解两个子问题，即找出s1[i-1]和s2[j]的一个最长公共子序列及s1[i]和s2[j-1]的一个最长公共子序列。这两个公共子序列中较长者为s1和s2的一个最长公共子序列。

4.代码
时间复杂度O(mn),m,n是两个字串长度

#include <iostream>
#include <cstring>
using namespace std;char sz1[1000];
char sz2[1000];
int maxLen[1000][1000];
int main()
{while(cin>>sz1>>sz2){int length1=strlen(sz1);int length2=strlen(sz2);int i,j;for(i=0;i<length1;i++)maxLen[i][0]=0;for(j=0;j<length2;j++)maxLen[0][j]=0;for(i=1;i<=length1;i++){for(j=1;j<=length2;j++)if(sz1[i-1]==sz2[j-1])maxLen[i][j]=maxLen[i-1][j-1]+1;elsemaxLen[i][j]=max(maxLen[i][j-1],maxLen[i-1][j]);}cout<<maxLen[length1][length2]<<endl;}return 0;
}

例题二：最大子段和

1.描述

由n个整数（包含负整数）组成的序列a1,a2,...,an，求该序列子段和的最大值。

规定当所有整数均为负值时定义其最大子段和为0。

否则所求的最大值为

例如，当(a1,a2, ……a7,a8)=(1,-3, 7,8,-4,12, -10,6)时， 最大子段和为：7+8-4+12=23

2.思路

设b[j]是从a[1]到a[j]位置的最大子段和(必须以a[j]结尾)

当b[j-1]>0时b[j]=b[j-1]+a[j]，否则b[j]=a[j]

　

1

2

3

4

5

6

a[i]

-2

11

-4

13

-5

-2

b(初值=0)

-2

11

7

20

15

13

sum

0

11

11

20

20

20

3.代码

#include <iostream>
#include <algorithm>
using namespace std;
const int MAX=10000;
int main()
{int n;cin>>n;int a[MAX],b[MAX];for(int i=1;i<=n;i++){cin>>a[i];b[i]=0;//以a[i]为结尾的最大子段和}for(int i=1;i<=n;i++){if(b[i-1]>0)b[i]=b[i-1]+a[i];elseb[i]=a[i];}int m=*max_element(b+1,b+n+1);cout<<max(m,0)<<endl;return 0;
}

例题三：最长上升子序列(最长单调递增)

1.描述

一个数的序列ai，当a1 < a2 < ... < ag的时候，我们称这个序列是上升的。比如，对于序列(1，7，3，5，9，4，8)，有它的一些上升子序列，如(1，7)，(3，4，8)等等。这些子序列中最长的长度是4，比如子序列(1，3，5，8)。

2.输入

第一行是序列的长度N (1 <= N<=1000）。给出序列中的N个整数，这些整数的取值范围都在0到10000。

3.输出

最长上升子序列的长度

4.输入样例

7

1 7 3 5 9 4 8

5.输出样例

4

6.思路

（1）子问题

求以a[k] (k=1，2，3…N) 为终点的最长上升子序列的长度

一个上升子序列中最右边的那个数，称为该子序列的“终点”。

虽然这个子问题和原问题形式上并不完全一样，但是只要这N个子问题都解决了，那么这N个子问题的解中，最大的那个就是整个问题的解。

（2）确定状态

子问题只和一个变量——数字的位置相关。

因此序列中数的位置k就是“状态”，而状态k对应的“值”，就是以a[k]为“终点”的最长上升子序列的长度。状态一共有N个。

（4）状态转移方程

maxLen (k) 表示以a[k]为“终点”的最长上升子序列的长度，那么：

初始状态: maxLen (1) = 1

  • maxLen(k)=max{maxLen(i)：1<=i<k且a[i]<a[k]且k≠1}+1。
    • maxLen(k)就是起点在a[k]左边，终点数值小于a[k]，且长度最大的那个上升子序列的长度再加1。此处的的1就是a[k]本身，因为a[k]左边任何终点小于a[k]的子序列，加上a[k]后就能形成一个更长的上升子序列。
  • 若找不到这样的i，则maxLen(k) = 1

为了保证上升子序列尽可能的长，那么就有 dp[ i ]  尽可能的大， 但是在保证 dp[ i ] 尽可能大的基础上，还必须满足序列的上升； 所以 dp[ i ] = max ( 1 , dp[ j ] + 1 ) {  j < i && a[j] < a[i] } 。

  • 这里的1是：当 a[i] 前面的数都比他大的时候，他自己为一个子序列；
  • dp[ j ] + 1 指的是： 当第 i 个数前面有一个 第 j 个数满足 a[j]  <  a[i]  并且 j < i 这时候就说明 a[i] 可以接在 a[j] 后增加子序列的长度。

将 j 从 1 遍历到 i - 1，在这之间，找出尽可能大的dp[ i ]即为最长上升子序列的长度

dp[n] 不一定是最长的子序列，n是数的个数，例如序列 [ 2, 3, 4, 5, 1 ]，dp[5] = 1(由子序列[1]构成)，然而 dp[4] = 4(由子序列 [2,3,4,5] 构成) )

举个例子：一个序列（7， 9， 6， 10， 7， 1， 3）分别为 （a1, a2, a3, a4, a5, a6, a7）

  • 最开始a1 = 7,  令dp[ 1 ] = 1；
  • 再看a2 = 9，令dp[ 2 ] = 1，那么需要检查a2前面的元素是否有比他小的
    • 因为 a1 < a2 而且 dp[ 1 ] + 1 > dp[ 2 ], 所以dp[ 2 ] = dp[ 1 ] + 1 == 2;
  • 再看a3 = 6，令 dp[ 3 ] = 1, 那么需要检查a3前面的元素a1、a2是否有比他小的
    •  一看没有，那么到目前为止，子序列就是他自己。
  • 再看a4 = 10，令 dp[ 4 ] = 1，那么需要依次检查前面的元素 a1与 a2与 a3是否有比他小的 ,
    • 先看a1，a1<a4，而且dp[ 1 ] + 1 > dp[ 4 ]，所以dp[ 4 ] = dp[ 1 ] + 1 == 2，说明此时 a1 与 a4 可以构成一个长度为 2 的上升子序列
    • 再看a2 , a2 < a4，而且dp[ 2 ] + 1 == 3 > dp[ 4 ] == 2，所以dp[ 4 ] = dp[ 2 ] + 1 == 3,  即a4承接在a2后面比承接在a1后更好，承接在a2后面的序列为：a1 a2 a4 ，构成一个长度为 3 的上升子序列
    • 然后再来看 a3 , a3 < a4 但是 d[ 3 ] + 1 == 2  < dp[ 4 ] == 3 ,  所以呢就不能把a4加在a3的后面 。

7.代码：

 max(a,b):返回a,b两者之间的较大值
 max_element(r, r+6):返回数组r中[0, 6)之间的最大值的迭代器

#include <iostream>
#include <algorithm>
using namespace std;const int MAX=1010;
int a[MAX];
int maxLen[MAX];
int main()
{int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];maxLen[i]=1;}//每次求以第i个数为终点的最长上升子序列的长度for(int i=2;i<=n;i++){//查看以第j个数为终点的最长上升子序列for(int j=1;j<i;j++)if(a[i]>a[j])maxLen[i]=max(maxLen[i],maxLen[j]+1);}cout<<*max_element(maxLen+1,maxLen+n+1);return 0;
}


 

 例题四：数字三角形

1.描述

在上面的数字三角形中寻找一条从顶部到底边的路径，使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或右下走。
三角形的行数大于1小于等于100，数字为0- 99

 2.输入格式:
 5//三角形行数。下面是三角形

3.输出格式：

30//路径最大和

用二维数组的下三角存放数字三角形（数字三角形的最后一行可以直接存储到D[i][j]中）
D[i][j] ：第i行第j个数字(i,j从1开始算)
MaxSum(i, j)：从D[i][j]到底边的各条路径长
问题转化为求MaxSum(1,1)

D[i][j]出发，下一步只能走D[i+1][j]或者D[i+1][j+1]

（1）故对于N行的三角形，运用递归:

if (i==N)MaxSum(i,j) = D[i][j];//最后一行
elseMaxSum(i,j) = Max{MaxSum(i+1,j),MaxSum(i+1,j+1)}+ D[i][j];

因此，数字三角形的递归程序如下

#include <iostream>
#include <algorithm>#define MAX 101
using namespace std;int D[MAX][MAX];
int n;int MaxSum(int i,int j){if(i==n)return D[i][j];int x=MaxSum(i+1,j);//递归int y=MaxSum(i+1,j+1);return max(x,y)+D[i][j];
}int main()
{int i,j;cin>>n;for(i=1;i<=n;i++)for(j=1;j<=i;j++)cin>>D[i][j];cout<<MaxSum(1,1)<<endl;return 0;
}

但这个程序里有大量重复计算，时间复杂度为2^n

（2）改进：

如果每算出一个MaxSum(i,j)就保存起来，下次用到其值的时候直接取用，则可免去重复计算。因为三角形的数字总数是n*(n+1)/2，那么可以用O(n^2)时间完成计算。

#include <iostream>
#include <algorithm>#define MAX 101
using namespace std;int D[MAX][MAX];
int maxSum[MAX][MAX];
int n;int MaxSum(int i,int j){if(maxSum[i][j]!=-1)return maxSum[i][j];if(i==n)maxSum[i][j]=D[i][j];else{int x=MaxSum(i+1,j);int y=MaxSum(i+1,j+1);maxSum[i][j]=max(x,y)+D[i][j];}return maxSum[i][j];}int main()
{int i,j;cin>>n;for(i=1;i<=n;i++)for(j=1;j<=i;j++){cin>>D[i][j];maxSum[i][j]=-1;}cout<<MaxSum(1,1)<<endl;return 0;
}

（3）递归转为递推

 递推过程：

  • 格子中的数字代表此数到底边的路径最大值，可知最后一行到底边的最大值是数字本身

  • 倒数第二行中的第一个数字2，到底边路径的最大值就是max(4,5)+2，即7，同理可算出其它格子中的数字

空间优化：

没必要用二维maxSum数组存储每一个MaxSum(rj)，只要从底层一行行向上递推，那么只要一维数组maxSum[100]即可，即只要存储一行的MaxSum值就可以。

进一步考虑，连maxSum数组都可以不要，直接用D的第n行替代maxSum即可。

节省空间，时间复杂度不变

#include <iostream>
#include <algorithm>
using namespace std;
#define MAX 101
int D[MAX][MAX];
int n;
int *maxSum;
int main()
{int i,j;cin>>n;for(i=1;i<=n;i++)for(j=1;j<=i;j++)cin>>D[i][j];maxSum=D[n];for(int i=n-1;i>=1;i--)for(int j=1;j<=i;j++)maxSum[j]=max(maxSum[j],maxSum[j+1])+D[i][j];cout<<maxSum[1]<<endl;return 0;
}

例题五 0-1背包问题

详解在我的另一篇博客

应用题

应用一：合唱队形（最长递增、递减序列）

1.描述

N位同学站成一排，音乐老师要请其中的(N-K)位同学出列，使得剩下的K位同学排成合唱队形。合唱队形是指这样的一种队形：设K位同学从左到右依次编号为1，2…，K，他们的身高分别为T1，T2，…，TK，  则他们的身高满足T1<...<Ti>Ti+1>…>TK(1<=i<=K)。已知所有N位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

2.输入

输入的第一行是一个整数N(2<=N<=100)，表示同学的总数。 第二有N个整数，用空格分隔，第i个整数Ti(130<=Ti<=230)是第i位同学的身高(厘米)。

3.输出

输出最少需要几位同学出列。

4.样例输入

8
186 186 150 200 160 130 197 220

5.样例输出

4

6.思路

选中队列中的一个学生，以该学生为核心，分别求出其左侧的最长递增子序列和其右侧的最长递减子序列，两者相加，再减去1就是以该同学为中心的合唱队的人数

我们只需把每个学生都作为中心遍历一遍，就能得出人数最多的合唱队形，再把总人数减去合唱人数就是需要剔除的人数。

7.代码

#include <iostream>
#include <algorithm>
#include <cstdio>using namespace std;
const int MAX=110;
int hign[MAX];
int maxLen[MAX];
int minLen[MAX];
int s1[MAX]={0};
int s2[MAX]={0};
int main()
{int n,sum=0;scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&hign[i]);maxLen[i]=1;minLen[i]=1;}//以第k个学生为中心，k=1~nfor(int k=2;k<=n;k++){for(int i=2;i<=k;i++){for(int j=1;j<i;j++)if(hign[i]>hign[j])maxLen[i]=max(maxLen[i],maxLen[j]+1);s1[i]=max(maxLen[i],s1[i]);}for(int i=k+1;i<=n;i++){for(int j=k;j<i;j++)if(hign[i]<hign[j])minLen[i]=max(minLen[i],minLen[j]+1);s2[i]=max(minLen[i],s2[i]);}}for(int i=1;i<=n;i++)sum=max(s1[i]+s2[i]-1,sum);printf("%d",n-sum);return 0;
}

应用二：数塔问题（数字三角形）

1.描述

设有一个三角形的数塔，顶点为根结点，每个结点有一个整数值。从顶点出发，可以向左走或向右走，如图所示：

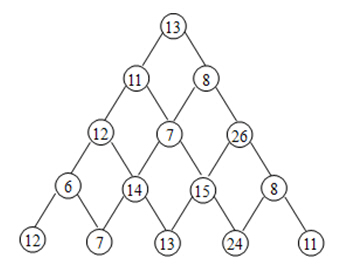
若要求从根结点开始，请找出一条路径，使路径之和最大，只要输出路径的和。

2.输入

第一行为n(n<50)，表示数塔的层数
从第2行至n+1行，每行有若干个数据，表示数塔中的数值。

3.输出

最大的路径值。

4.样例输入

5
13
11  8
12  7  26
6  14  15  8
12  7  13  24  11

5.样例输出

86

6.思路

用一个二维数组a存储数塔的原始数据（其实我们只使用数组a一半的空间，一个下三角矩阵）

用一个二维数组dp存储每一次决策过程中的结果（也是一个下三角矩阵）

初始化dp，将a的最后一层拷贝到dp中：dp[n][j] = a[n][j] (j = 1, 2, …, n) 其中，n为数塔的层数

递归填上dp数组的值，dp[i][j] = max(dp[i+1][j], dp[i+1][j+1]) + a[i][j]，最后的结果保存在dp[0][0]中

7.代码

#include <iostream>
#include <cstdio>
using namespace std;const int MAX=55;
int a[MAX][MAX];
int dp[MAX][MAX];
int main()
{int n,tmax;scanf("%d",&n);for(int i=1;i<=n;i++)for(int j=1;j<=i;j++)scanf("%d",&a[i][j]);//初始化dp数组最后一行for(int i=1;i<=n;i++)dp[n][i]=a[n][i];//递归从下到上求dp数组for(int i=n;i>0;i--){for(int j=1;j<=i;j++){tmax=max(dp[i+1][j],dp[i+1][j+1]);dp[i][j]=tmax+a[i][j];}}printf("%d",dp[1][1]);return 0;
}


http://chatgpt.dhexx.cn/article/vR8njqEF.shtml

相关文章

动态规划 DP专题

动态规划 DP专题

跟着ygg的dp题单刷的dp 1.代码源每日一题 Div1 连续子序列 分析&#xff1a; dp数组开成map&#xff0c;则状态转移式dp[i] max(dp[i - 1] 1, dp[i]) AC代码&#xff1a; #include <bits/stdc.h>using namespace std; typedef long long ll; #define int ll #define …
阅读更多...
动态规划之线性DP

动态规划之线性DP

&#x1f40f;&#x1f40f;&#x1f40f; &#x1f40f;动态规划之线性DP&#x1f40f;&#x1f40f;写在前面&#x1f40f;&#x1f40f;数字三角形&#x1f40f;&#x1f40f;最长上升子序列&#x1f40f;&#x1f40f;最长上升子序列 II&#x1f40f;&#x1f40f;最长公共…
阅读更多...
DP（动态规划）入门基础详解

DP（动态规划）入门基础详解

DP总结&#xff08;写得这么辛苦点个赞呗&#xff01;&#xff09; DP基本概要&#xff1a; 动态规划算法把原问题视作若干个重叠子问题的逐层递进,每一个子问题的求解过程都构成一个“阶段”。在完成前一个阶段的计算后,动态规划才会执行下一阶段的计算。 无后效性 &#xf…
阅读更多...
非常好的动态规划（DP）总结

非常好的动态规划（DP）总结

转自&#xff1a; http://cppblog.com/menjitianya/archive/2015/10/23/212084.html 目录 一、动态规划初探 1、递推 2、记忆化搜索 3、状态和状态转移 4、最优化原理和最优子结构 5、决策和无后效性 二、动态规划的经典模型 1、线性模型 2、区间模型 3、背包模型 4、状态压…
阅读更多...
动态规划 DP （一）

动态规划 DP （一）

1.动态规划&#xff08;Dynamic Programming&#xff0c;简称DP&#xff09; 维基百科的定义说的很清楚&#xff1a; 动态规划不能解决所有的问题&#xff0c; 只能应用于有最优子结构的问题。例如背包问题、最长公共子序列问题、最短路径问题等。 最优子结构&#xff1a;局部…
阅读更多...
动态规划（DP）通俗讲解

动态规划（DP）通俗讲解

参考 徐凯强 Andy 动态规划中递推式的求解方法不是动态规划的本质。 我曾经作为省队成员参加过NOI&#xff0c;保送之后也给学校参加NOIP的同学多次讲过动态规划&#xff0c;我试着讲一下我理解的动态规划&#xff0c;争取深入浅出。希望你看了我的答案&#xff0c;能够喜欢上动…
阅读更多...
【算法之动态规划（一）】动态规划（DP）详解

【算法之动态规划（一）】动态规划（DP）详解

一、基本概念 动态规划(dynamic programming)是 运筹学 的一个分支&#xff0c;是求解决策过程(decision process)最优化的数学方法。20世纪50年代初 美国 数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时&#xff0c;提出了著名的最优…
阅读更多...
动态规划(dp)的总结

动态规划(dp)的总结

动态规划(dp)的总结 动态规划只要找到子问题&#xff0c;写起来就很简单&#xff0c;通常最多就二维dp数组即可解决问题&#xff0c;顶多再来个双dp&#xff0c;再加点逆向思维……下面列出我见过的子问题&#xff0c;别栽在dp上了&#xff0c;求求了。 能用dp做&#xff0c;…
阅读更多...
数据结构与算法——动态规划（DP）

数据结构与算法——动态规划（DP）

文章目录 1. 应用场景2. DP状态2.1 最优子结构2.2 无后效性2.3 解题思路 3. 问题类别3.1 线性DP3.1.1 经典问题3.1.1.1 [LeetCode 300. 最长上升子序列](https://leetcode-cn.com/problems/longest-increasing-subsequence/)3.1.1.2 [LeetCode 1143. 最长公共子序列](https://l…
阅读更多...
关于动态规划（dp）

关于动态规划（dp）

**动态规划(DP) 一.基本概念 动态规划&#xff08;英语&#xff1a;Dynamic programming&#xff0c;简称DP&#xff09;是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的&#xff0c;通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。 它针对满足…
阅读更多...
动态规划（DP）的原理、实现及应用

动态规划（DP）的原理、实现及应用

文章目录 1. 由一个例子说开&#xff1a; 斐波那契&#xff08;fibonacci&#xff09;数列 性能测试原因分析2. 记忆化搜索3. 动态规划&#xff08;Dynamic Programming&#xff0c;DP&#xff09; 最优子结构总结一下这几个解法&#xff1a;几个例题 LeetCode 70 Climbing St…
阅读更多...
Hi3519AV100与Hi3559AV100在芯片规格 上主要差异

Hi3519AV100与Hi3559AV100在芯片规格 上主要差异

表1-1简要对比了Hi3519AV100与Hi3559AV100在规格方面的差异&#xff0c;Hi3519AV100的具体规格请参见《Hi3519AV100 ultra-HD Mobile Camera SoC 用户指南》。
阅读更多...
海思平台（hi3559av100）异构多系统的使用Linux（2*A53+2*A73）+liteos（A53）+liteos（M7）

海思平台（hi3559av100）异构多系统的使用Linux（2*A53+2*A73）+liteos（A53）+liteos（M7）

在文档《SDK安装及升级使用说明》中有对linuxliteos异构多系统的烧写有介绍。这里对其中的一些注意的地方记录以下&#xff0c;以备查验。 由于我的目标是要搭建一个ISP调试环境&#xff0c;就是使用海思的ittp_stream工具能够连接上开发板&#xff0c;并能够实时查看摄像头的…
阅读更多...
M302H-ZN-Hi3798MV300／MV300H-当贝纯净桌面-卡刷固件包

M302H-ZN-Hi3798MV300／MV300H-当贝纯净桌面-卡刷固件包

M302H-ZN-Hi3798MV300&#xff0f;MV300H-当贝纯净桌面-卡刷固件包-内有教程 特点&#xff1a; 1、适用于对应型号的电视盒子刷机&#xff1b; 2、开放原厂固件屏蔽的市场安装和u盘安装apk&#xff1b; 3、修改dns&#xff0c;三网通用&#xff1b; 4、大量精简内置的没用…
阅读更多...
华为海思 hikey970 详细介绍

华为海思 hikey970 详细介绍

前几天申请到了华为的开发板&#xff1a;hikey970 用来做项目的。 板子是这样的: 下面是在网中收集到的信息总结&#xff1a; 基于麒麟970的AI智慧算力&#xff0c;HiKey 970除了支持CPU和GPU的AI运算外&#xff0c;还支持基于NPU的神经网络计算硬件加速。 公开资料显示&am…
阅读更多...
海思Hi3519AV100 emmc flash方式 linux系统移植 hitool工具烧写

海思Hi3519AV100 emmc flash方式 linux系统移植 hitool工具烧写

因为我这里的海思文档只有SPI NOR Flash方式的详细烧写步骤&#xff0c;没有emmc方式的&#xff0c;本文提供一个自己成功的案例仅供参考和记录 1. 准备SDK、安装交叉编译工具、编译osdrv 1.1 解压SDK包 将Hi3519AV100_SDK_Vx.x.x.x.tgz文件放入ubuntu系统下&#xff08;wind…
阅读更多...
海思3559：MMZ内存、OS内存配置

海思3559：MMZ内存、OS内存配置

前言 海思3559的DDR最大支持到8GB hi3559av100芯片的内存地址范围 (1)通过查阅数据手册可知《Hi3559AV100 专业型 Smart IP Camera SoC 用户指南》&#xff0c;芯片的内存地址范围是0x4000_0000-0x23FFF_FFFF&#xff0c;最大能支持8G内存&#xff1b;   (2)海思芯片把内存分…
阅读更多...
劲爆！java架构师百度网盘

劲爆！java架构师百度网盘

第一份资料：Kafka实战笔记 Kafka入门为什么选择KafkaKarka的安装、管理和配置Kafka的集群第一个Kafka程序afka的生产者 Kafka的消费者深入理解Kafka可靠的数据传递
阅读更多...
10本Java架构师必读书籍推荐

10本Java架构师必读书籍推荐

##### 1.《大型网站系统与Java中间件开发实践》 本书围绕大型网站和支撑大型网站架构的 Java 中间件的实践展开介绍。从分布式系统的知识切入&#xff0c;让读者对分布式系统有基本的了解&#xff1b;然后介绍大型网站随着数据量、访问量增长而发生的架构变迁&#xff1b;接着…
阅读更多...
Java架构师需要哪些知识？

Java架构师需要哪些知识？

如何才能达到Java架构师技术要求标准&#xff1f;Java架构师需要熟练掌握复杂的数据结构和算法、熟练使用linux操作系统&#xff0c;Linux线上排除故障、熟悉tcp协议、系统集群、[负载均衡]、反向代理、动静分离&#xff0c;网站静态化、数据库设计能力、队列中间件等知识。 一…
阅读更多...
推荐文章

Copyright @ 2022~2023