动态规划（DP）

文章目录

动态规划（DP）
- 1.动态规划概念
- 2.最短路径问题
- 3.动态规划和分治区别
- 4.为什么动态规划往往从后往前？

1.动态规划概念

在现实生活中，有一类活动的过程，由于它的特殊性，可将过程分成若干个互相联系的阶段，在它的每一阶段都需要作出决策，从而使整个过程达到最好的活动效果。因此各个阶段决策的选取不能任意确定，它依赖于当前面临的状态，又影响以后的发展。当各个阶段决策确定后，就组成一个决策序列，因而也就确定了整个过程的一条活动路线．这种把一个问题看作是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程，这种问题称为多阶段决策问题。在多阶段决策问题中，各个阶段采取的决策，一般来说是与时间有关的，决策依赖于当前状态，又随即引起状态的转移，一个决策序列就是在变化的状态中产生出来的，故有“动态”的含义，称这种解决多阶段决策最优化的过程为动态规划方法

动态规划核心思想：化繁为简，将大问题拆解成一堆小问题，该小问题的解会被重复调用，动态规划通过保存子问题最优解，避免了重复计算，提高了效率，降低时间复杂度，但同时增加了空间复杂度。

2.最短路径问题

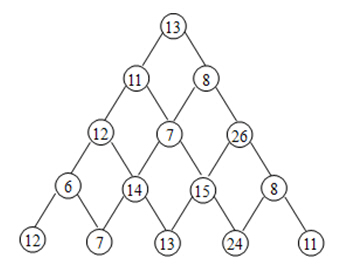
问题描述：给定一个矩阵m，从左上角开始每次只能（上下左右）走一步，如遇边界则不可走，最后达到右下角的位置，路径中所有数字累加起来就是路径和，返回所有路径的最小路径和。
在这里插入图片描述

为方便描述按XY方向编号，假设从起始点（0,0）到目标点（4,4）需要走n步（在不考虑回头的情况下，不选择已经走过的路，从表格中可以看出总共就是走6步），每一步路径长度对应表格中的数值，记为 ${C_n}$ ，每一步在p位置上对应的总路径长度 ${f_{(p)}}(n)$ ，直接看一下动态规划的过程。

动态规划过程:

从目标终点往回看。
n = 6
${f_{(4,4)}}(6) = 0$ ，从目标点（4,4）出发，有两个选择。

n = 5

${f_{(3,4)}}(5) = {f_{(4,4)}}(6) + 1=1$
${f_{(4,3)}}(5) = {f_{(4,4)}}(6) + 4=4$
在这里插入图片描述

n=4

对于（3,3），可以从（4,3）到达，总路径为： ${f_{(4,3) \to (3,3)}}(5) = {f_{(4,3)}}(5) + 6=10$
也可以从(3,4)到达，总路径为： ${f_{(3,4) \to (3,3)}}(5) = {f_{(3,4)}}(5) + 1=7$
显然，想要从目标点（4,4）到达（3,3），最优的选择是从（3,4）这一点，所以放弃另外路线。
${f_{(2,4)}}(4) = {f_{(3,4)}}(5) + 2=3$
${f_{(3,3)}}(4) = {f_{(3,4)}}(5) + 6=7$
${f_{(4,2)}}(4) = {f_{(4,3)}}(5) + 8=12$
在这里插入图片描述

到这里其实动态规划的优势已初见端倪，我们将整个大的问题，切分成了若干个小的子问题，通过迭代的方式依次求出子问题最优解，所有子问题的最优解之和不一定是全局最优解，但全局最优解一定包含着若干局部最优解。当我们计算每一阶段的目标函数 $f (n)$ 时，只需要用上一阶段的目标函数值加上对应路径长度，即 $f (n) = f (n + 1) + C (n)$ 。
你可能会说：“这有啥，跟暴力搜索有啥区别？”
示例很简单，可以一眼看出下一节点的目标函数值 $f (n)$ ，想象一下如果f(6)后面还有10万个节点，那么每一次前进都要遍历一遍前面的路径，这包含了很多重复的计算，计算量也是无法接受的。可以想象如果要从（3,3）前往（4,4）（子问题），中间有很多条路线，我们只需要计算一遍并记住最短的一条（最优解）即可，从而避免了重复的计算（搜索）。
在这里插入图片描述
小结一下，动态规划通过将问题切分，化繁为简，使得每一个子问题小到可以轻松计算，记录节点（子问题的最优解）的值，快速迭代产生下一节点的值，免去了重复的计算（搜索）。当然这也付出一定代价，需要（内存）记住节点上所有的可行解，当可行解多到（内存）记不住时，这又是另一话题了。

动态规划算法的关键在于解决冗余，这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术，它在实现的过程中，不得不存储产生过程中的各种状态，所以它的空间复杂度要大于其他的算法。选择动态规划算法是因为动态规划算法在空间上可以承受，而搜索算法在时间上却无法承受，所以我们舍空间而取时间。

n=3
同理，根据 $f (n) = f (n + 1) + C (n)$ 依次计算各个目标函数值。
${f_{(1,4)}}(3) = {f_{(2,4)}}(4) + 9=12$
${f_{(2,3)}}(3) = {f_{(2,4)}}(4) + 3=6$
${f_{(3,2)}}(3) = {f_{(3,3)}}(4) + 1=8$
${f_{(4,1)}}(3) = {f_{(4,2)}}(4) + 8=20$
在这里插入图片描述
n=2
${f_{(1,3)}}(2) = {f_{(2,3)}}(3) + 5=11$
${f_{(2,2)}}(2) = {f_{(2,3)}}(3) + 1=7$
${f_{(3,1)}}(2) = {f_{(3,2)}}(3) + 5=13$

n=1
${f_{(1,2)}}(1) = {f_{(2,2)}}(2) + 3=10$
${f_{(2,1)}}(1) = {f_{(2,2)}}(2) + 6=13$

至此，可以得到最短路径：0-3-1-3-2-1-0， $f = 10$
在这里插入图片描述

3.动态规划和分治区别

动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
动态规划算法：它通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。

分治法：若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。我们可以用一个表来记录所有已解的子问题的答案。

总而言之就是，只要之前计算过的结果，动态规划都会保存结果，而再次用到时不会再算一遍，而是直接调用结果。