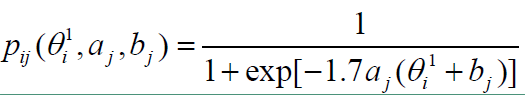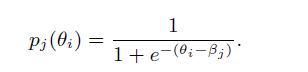多维IRT模型的EM估计

MIRT （Multidimensional Item Response Theory）多维项目反应理论。与一维项目反应理论的区别只是在于对于潜在变量的${\theta }_i$ 的建模，一个是unidimensional latent trait ${\theta }_i$，一个是multidimensional ${\mathbf{\theta }}_{\mathbf{i}}=c({\theta }_{i1},{\theta }_{i2},\dots ,{\theta }_{iK})$，这里$K$ 就是MIRT 中所指代的维数。以下是M2PL(Multidimensional Two Parameter Logistic) 模型的似然函数。
-0. Notation 记号如下，
假设有$N$ 个被试参加了一个有$J$ 个题目的测试，获得对应的二值反应数据$Y=(Y_{ij}{)}_{i=1,j=1}^{N,J}$，其中$Y_{ij}=1$ 表示第$i$ 个人答对了第$j$ 个题目，否则$Y_{ij}=0$。假设这个测试中，每个题目$j$ 测试了$K$ 种能力，对应了$K$ 个区分度参数${\mathbf{a}}_{\mathbf{j}}^{{}^{\prime }}=c(a_{j1},a_{j2},\dots ，a_{jK})$，一个难度参数的等价参数$d_j$，相对应的，每个被试$i$ 在作答题目的时候就对应了$K$ 种能力，也就是${\mathbf{\theta }}_{\mathbf{i}}=c({\theta }_{i1},{\theta }_{i2},\dots ,{\theta }_{iK})$。记项目参数为$A=({\mathbf{a}}_{\mathbf{j}}^{{}^{\prime }}{)}_{j=1}^J$, $\mathbf{d}=(d_j{)}_{j=1}^J$, $\Theta =({\mathbf{\theta }}_{\mathbf{i}}^{{}^{\prime }}{)}_{i=1}^N$.

-1. Likelihood function of M2PLM
$$L(Y;A,\mathbf{d},\Theta )=\prod _{i=1}^N\prod _{j=1}^J\frac{exp(Y_{ij}({\mathbf{a}}_{\mathbf{j}}^{{}^{\prime }}{\mathbf{\theta }}_{\mathbf{i}}+d_j))}{1+exp({\mathbf{a}}_{\mathbf{j}}^{{}^{\prime }}{\mathbf{\theta }}_{\mathbf{i}}+d_j)}.$$

-2. Identification for MIRT
在IRT模型中，对于不同的人，一般假设答题独立，并且能力$\theta$ 服从相同的或者一元或者多元正态分布。在一维IRT模型中，一般为了模型可识别，只需要限制人的能力${\theta }_i$ 服从均值和方差都已知的正态分布。一般使用$N(0,1)$。在MIRT模型中也需要限制人的多维度能力${\mathbf{\theta }}_{\mathbf{i}}$ 服从均值向量和方差协方差矩阵都是已知的多元正态分布，$N(\mathbf{\mu },\mathbf{\Sigma })$。除此之外，对于${\sum }_{k=1}^K{a}_{jk}{\theta }_{ik}+d_j$，考虑区分度参数${\mathbf{a}}_{\mathbf{j}}=(a_{j1},a_{j2},\dots a_{jK}{)}^{{}^{\prime }}$ 是可以旋转rotation，可以得到相同的量。因此在多维IRT模型中，为了模型的可识别，除了对于能力参数的限制，还要限制项目参数。
常用的限制有两种，Beguin and Glas (2001) 总结的有以下两种，

• Fraser, 1988, 提出的在探索性分析中，设置能力参数均值为0，方差为单位矩阵。项目参数满足限制${\alpha }_{jk}=0$，对于$j=1,2,\dots ,K-1$，$k=j+1,\dots ,K$。也就是对于前K-1个题目的区分度参数，限制为下三角矩阵。
• 将能力参数$\theta$看成是未知的被估计量(estimands)。可识别性的限制是设置前$K$个题的$d_j=0$，$j=1,2,\dots ,K$。而且对于前$K$个题的区分度参数${\alpha }_{jk}$，$j=1,2,\dots ,K$，如果$j=k$，则${\alpha }_{jk}=1$，否则${\alpha }_{jk}=0$。也就是说，前$K$个题的区分度参数是单位矩阵，并且是难度参数等价参数也是0。

Beguin and Glas (2001) 也推算出这两种可识别性的方法实际上是等价的，相差一个矩阵乘积的rotation。以上两种方法具体可以参考，Beguin and Glas (2001); Fraser & McDonald (1988); Jorekog (1969); Bolt & Lall (2003); Cai (2010); Jianan Sun, Yunxiao Chen et. al. (2016)。

-3. EM algorithm for M2PL

• Marginal Likelihood function is as follows,
  $$log{\int }_{\Theta }L(Y;A,\mathbf{d},\Theta )d\Theta =\sum _{i=1}^{N}log{\int }_{{\mathbf{\theta }}_{\mathbf{i}}}L(Y_{i.};A,\mathbf{d},{\mathbf{\theta }}_{\mathbf{i}})g({\mathbf{\theta }}_{\mathbf{i}})d{\mathbf{\theta }}_{\mathbf{i}},$$
  其中，$g({\mathbf{\theta }}_{\mathbf{i}})\sim N(0,{\mathbf{I}}_{K\times K})$ 是${\mathbf{\theta }}_{\mathbf{i}}$ 的先验函数。

• Gradient of parameter ${\mathbf{a}}_{\mathbf{j}}^{{}^{\prime }}$ is as follows,
  $$\frac{\partial }{\partial {\mathbf{a}}_{\mathbf{j}}^{{}^{\prime }}}log{\int }_{\Theta }L(Y;A,\mathbf{d},\Theta )d\Theta$$
  $$=\sum _{i=1}^N{\int }_{{\mathbf{\theta }}_{\mathbf{i}}}\frac{{\prod }_{j=1}^{J}L(Y_{ij};{\mathbf{a}}_{\mathbf{j}},d_j,{\mathbf{\theta }}_{\mathbf{i}})g({\mathbf{\theta }}_{\mathbf{i}})}{{\int }_{{\mathbf{\theta }}_{\mathbf{i}}}{\prod }_{j=1}^{J}L(Y_{ij};{\mathbf{a}}_{\mathbf{j}},d_j,{\mathbf{\theta }}_{\mathbf{i}})g({\mathbf{\theta }}_{\mathbf{i}})d{\mathbf{\theta }}_{\mathbf{i}}}\frac{\partial }{\partial {\mathbf{a}}_{\mathbf{j}}^{{}^{\prime }}}log\prod _{j=1}^{J}L(Y_{ij};{\mathbf{a}}_{\mathbf{j}},d_j,{\mathbf{\theta }}_{\mathbf{i}})d{\mathbf{\theta }}_{\mathbf{i}}$$
  因为${\mathbf{\theta }}_{\mathbf{i}}$ 的后验概率$P({\mathbf{\theta }}_{\mathbf{i}}|Y_{i.},A,\mathbf{d})=\frac{{\prod }_{j=1}^{J}L(Y_{ij};{\mathbf{a}}_{\mathbf{j}},d_j,{\mathbf{\theta }}_{\mathbf{i}})g({\mathbf{\theta }}_{\mathbf{i}})}{{\int }_{{\mathbf{\theta }}_{\mathbf{i}}}{\prod }_{j=1}^{J}L(Y_{ij};{\mathbf{a}}_{\mathbf{j}},d_j,{\mathbf{\theta }}_{\mathbf{i}})g({\mathbf{\theta }}_{\mathbf{i}})d{\mathbf{\theta }}_{\mathbf{i}}}$，并且导数可求。从而上式就变为，
  $$=\sum _{i=1}^N{\int }_{{\mathbf{\theta }}_{\mathbf{i}}}P({\mathbf{\theta }}_{\mathbf{i}}|Y_{i.},A,\mathbf{d})(Y_{ij}{\mathbf{\theta }}_{\mathbf{i}}-\frac{exp({\mathbf{a}}_{\mathbf{j}}^{{}^{\prime }}{\mathbf{\theta }}_{\mathbf{i}}+d_j)}{1+exp({\mathbf{a}}_{\mathbf{j}}^{{}^{\prime }}{\mathbf{\theta }}_{\mathbf{i}}+d_j)}{\mathbf{\theta }}_{\mathbf{i}})d{\mathbf{\theta }}_{\mathbf{i}}$$

• Substitute for integration using nodes $X_{i{k}_1},X_{i{k}_2},X_{i{k}_3}$, for $k_1,k_2,k_3=1,2,\dots ，q$这里假设考察的能力$K=3$, 则上述积分变为，
  $$=\sum _{i=1}^N\sum _{k_1=1}^q\sum _{k_2=1}^q\sum _{k_3=1}^{q}P({\mathbf{\theta }}_{\mathbf{i}}=c(X_{i{k}_1},X_{i{k}_2},X_{i{k}_3})|Y_{i.},A,\mathbf{d})(Y_{ij}\ast c(X_{i{k}_1},X_{i{k}_2},X_{i{k}_3}{)}^{{}^{\prime }}$$
  $$-\frac{exp({{\mathbf{a}}_{\mathbf{j}}}^{{}^{\prime }}c(X_{i{k}_1},X_{i{k}_2},X_{i{k}_3})+d_j)}{1+exp({{\mathbf{a}}_{\mathbf{j}}}^{{}^{\prime }}c(X_{i{k}_1},X_{i{k}_2},X_{i{k}_3})+d_j)}\ast c(X_{i{k}_1},X_{i{k}_2},X_{i{k}_3}{)}^{{}^{\prime }})$$

-4. EM program for simulation data

• Generate simulated data
  假设$N=3000$个人作答了$J=20$题，测试了$K=3$个能力，项目区分度参数${\mathbf{a}}_{\mathbf{j}}\sim runif(K,0,2)$, 难度参数等价参数$d_j\sim runif(1,-1,1)$, 能力参数${\theta }_{i1}\sim rnorm(1,0,1)$, ${\theta }_{i2}\sim rnorm(1,0,1)$, ${\theta }_{i3}\sim rnorm(1,0,1)$。根据M2PL生成数据，得到的前5个人的反应如下，
  
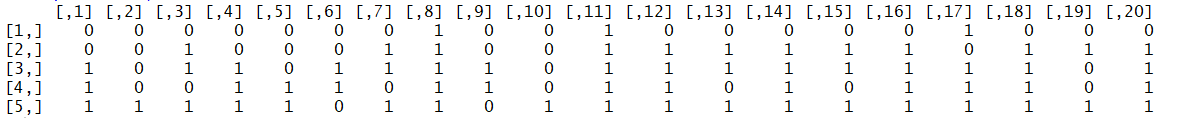
  生成代码如下，

####generate simulated data####
N <- 3000;J <- 20;K <- 3
theta_1 <- rnorm(N);theta_2 <- rnorm(N);theta_3 <- rnorm(N);theta_true <- cbind(rep(1,N),theta_1,theta_2,theta_3)
A_true <- matrix(0,J,K);A_true[1:10,1] <- runif(10,1,2);A_true[11:20,1] <- A_true[1:10,1]*1.5;A_true[1:10,2] <- runif(10,1.5,2);A_true[11:20,2] <- runif(10,0,0.5);A_true[1:10,3] <- runif(10,0,0.5);A_true[11:20,3] <- runif(10,1.5,2);
d_true <- runif(J,0,1)
D_true <- cbind(d_true,A_true)
P_true <- 1/(1+exp(-theta_true%*%t(D_true)))
response <- matrix(rbinom(N*J,1,P_true),nrow=N,ncol=J);#response
response[1:5,]

• Estimating the parameters in M2PL model
  – Using the function “mirt” from R package “mirt” as follows,

###mirt analysis###
library(mirt)
m2pl_mod <- 'F1 = 1-20
F2 = 1-19
F3= 1-18
COV = F1 * F2*F3'
m2pl_fit <- mirt(data = response, model = m2pl_mod,itemtype = "2PL", method = "EM",SE = TRUE)
m2pl_params <- coef(m2pl_fit, simplify = TRUE)
bb <- cbind(D_true,m2pl_params$items[,4],m2pl_params$items[,1:3])
colnames(bb)<-c("d_true","a1_true","a2_true","a3_true","d_estimator","a1_estimator","a2_estimator","a3_estimator")

以下是真值和估计的结果，MAE是0.2794661，$\mathbf{d}$ 的MAE是0.05971843，${\mathbf{a}}_{.1}$ 的MAE是0.5641373，${\mathbf{a}}_{.2}$ 的MAE是0.3748544，${\mathbf{a}}_{.3}$ 的MAE是0.1191544。

– 以下是我用GD算法估计的R code 和结果。MAE是0.1221731，$\mathbf{d}$ 的MAE是0.05969582，${\mathbf{a}}_{.1}$ 的MAE是0.1148704，${\mathbf{a}}_{.2}$ 的MAE是0.1575343，${\mathbf{a}}_{.3}$ 的MAE是0.1565919。结果大致一样。

###my code###
Q <- matrix(1,J,K);Q[J,2:3] <- 0;Q[(J-1),3] <- 0;
##initial value###
A_initial <- matrix(0,J,K);A_initial[,1] <- runif(J,1,2);A_initial[,2] <- runif(J,1,2);A_initial[,3] <- runif(J,1,2);
A_initial <- A_initial*Q;
d_initial <- rnorm(J,0,1);D_initial <- cbind(d_initial,A_initial);
KK <- 20;theta_min <- -4;theta_max <- 4;mm1 <- seq(theta_min,theta_max,(theta_max-theta_min)/KK);mm <- mm1[-1]
THETA_tuta <- matrix(0,nrow=KK*KK*KK,ncol=3);THETA_tuta[,3] <- rep(mm,KK*KK);
THETA_tuta[,2] <-rep(c(rep(1,KK)%*%t(mm)),KK);THETA_tuta[,1] <-c(rep(1,KK*KK)%*%t(mm))#针对K <- 3的theta分块,获取theta的分块
THETA_tuta <- cbind(rep(1,nrow(THETA_tuta)),THETA_tuta)theta_tmp <- rowSums(THETA_tuta[,2:4]*THETA_tuta[,2:4])/2
response <- t(response);A_0 <- t(D_initial)
cc <- exp(THETA_tuta%*%A_0%*%response-theta_tmp)/apply(1+exp((THETA_tuta%*%A_0)),1,prod);
theta_post <- sweep(cc, 2, colSums(cc), "/") 
log_lik_0 <- sum(log(colSums(cc)))
disA <- 0.5;m <- A_0
timstart <- Sys.time()
for(j in 1:J){A_grad <- c(c(theta_post%*%response[j,]-rowSums(theta_post*c(1/(1+exp(-THETA_tuta%*%A_0[,j])))))%*%THETA_tuta)step <- 1/50A_tuta <- A_0[,j]+step*A_grad;aa <- A_0;aa[,j] <- A_tuta;log_lik_1 <- sum(log(colSums(exp(THETA_tuta%*%aa%*%response-theta_tmp)/apply(1+exp((THETA_tuta%*%aa)),1,prod))));while(log_lik_1<log_lik_0+step*sum(A_grad*A_grad)*0.2){step <- step*disA;A_tuta <- A_0[,j]+step*A_grad;aa <- A_0;aa[,j] <- A_tuta;log_lik_1 <- sum(log(colSums(exp(THETA_tuta%*%aa%*%response-theta_tmp)/apply(1+exp((THETA_tuta%*%aa)),1,prod))));}m[,j] <- A_tuta
}
A_0 <- m*t(cbind(rep(1,J),Q))
log_lik_1 <- sum(log(colSums(exp(THETA_tuta%*%A_0%*%response-theta_tmp)/apply(1+exp((THETA_tuta%*%A_0)),1,prod))));
eps <- log_lik_1-log_lik_0
while(eps>0.001){log_lik_0 <- log_lik_1;cc <- exp(THETA_tuta%*%A_0%*%response-theta_tmp)/apply(1+exp((THETA_tuta%*%A_0)),1,prod);theta_post <- sweep(cc, 2, colSums(cc), "/") for(j in 1:J){A_grad <- c(c(theta_post%*%response[j,]-rowSums(theta_post*c(1/(1+exp(-THETA_tuta%*%A_0[,j])))))%*%THETA_tuta)step <- 1/50A_tuta <- A_0[,j]+step*A_grad;aa <- A_0;aa[,j] <- A_tuta;log_lik_1 <- sum(log(colSums(exp(THETA_tuta%*%aa%*%response-theta_tmp)/apply(1+exp((THETA_tuta%*%aa)),1,prod))));while(log_lik_1<log_lik_0+step*sum(A_grad*A_grad)*0.2){step <- step*disA;A_tuta <- A_0[,j]+step*A_grad;aa <- A_0;aa[,j] <- A_tuta;log_lik_1 <- sum(log(colSums(exp(THETA_tuta%*%aa%*%response-theta_tmp)/apply(1+exp((THETA_tuta%*%aa)),1,prod))));}m[,j] <- A_tuta}A_0 <- m*t(cbind(rep(1,J),Q))log_lik_1 <- sum(log(colSums(exp(THETA_tuta%*%A_0%*%response-theta_tmp)/apply(1+exp((THETA_tuta%*%A_0)),1,prod))));eps <- log_lik_1-log_lik_0
}
timend <- Sys.time()
tt <- timend-timstart
tt

[1]:Béguin, A. A., & Glas, C. A. (2001). MCMC estimation and some model-fit analysis of multidimensional IRT models. Psychometrika, 66(4), 541-561.
[2]:Fraser, C., & McDonald, R. P. (1988). NOHARM: Least squares item factor analysis. Multivariate behavioral research, 23(2), 267-269.
[3]:Jöreskog, K. G. (1969). A general approach to confirmatory maximum likelihood factor analysis. Psychometrika, 34(2), 183-202.
[4]:Bolt, D. M., & Lall, V. F. (2003). Estimation of compensatory and noncompensatory multidimensional item response models using Markov chain Monte Carlo. Applied Psychological Measurement, 27(6), 395-414.
[5]:Cai, L. (2010). High-dimensional exploratory item factor analysis by a Metropolis–Hastings Robbins–Monro algorithm. Psychometrika, 75(1), 33-57.
[6]:Sun, J., Chen, Y., Liu, J., Ying, Z., & Xin, T. (2016). Latent Variable Selection for Multidimensional Item Response Theory Models via L1 Regularization. psychometrika, 81(4), 921-939.