目录
一、有关贝叶斯的简介
二、相关数学知识
1.先验概率与后验概率
2.贝叶斯公式
3、最大后验概率
4、最大似然估计法
一、有关贝叶斯的简介
贝叶斯老爷子的名字,很多同学都耳熟能详。估计不少的同学都在数学上被贝叶斯折磨过。贝叶斯在数学方面主要研究概率论.对于统计决策函数、统计推断、统计的估算等做出了贡献。然而,贝叶斯也是属于那种生不逢时的科学家,他的生前一直默默无闻,直到他过世之后,他的著作和成果才陆陆续续的被发表出去,他本人也逐渐被世人所认可。向科学家致敬!salute!

二、相关数学知识
理解贝叶斯分类器之前,我们要先理解一定的数学知识,并且通过学习同学们要好好掌握贝叶斯在概率论上的成就。
1.先验概率与后验概率
我们先来看定义!
先验概率:在贝叶斯统计推断中,先验概率是在收集新数据之前事件发生的概率。 这是在进行实验之前根据当前知识对结果可能性进行的最佳理性评估。
后验概率:事件发生后求的反向条件概率;或者说,基于先验概率求得的反向条件概率。概率形式与条件概率相同。
看到这里,是不是感觉晦涩难懂?
那么我们举一个小小的例子来感受一下:
案例:伍老师所在的学校里,偏瘦和偏胖的人所占比例为6:4,并且此时学校封校,且学校不允许点外卖,只能去食堂吃饭。该校食堂中,只有两种伙食:荤菜与减脂餐。偏瘦的人觉得封校就要对自己好一点,于是只吃荤菜;而偏胖的人有一半想对自己好一点,也吃荤菜,另一半人想要减肥,选择吃减脂餐。
如果是想要我们求先验概率,出题者会这么问:
随机选一个在学校的幸运儿,请问他吃减脂餐的概率是多少?
然而如果是想让我们求后验概率,出题者的提问方式则变成了:
在学校餐厅的一个餐桌上有一盘荤菜,而他的主人恰逢上厕所去了,并且你不认识也从未听说过这个人,请问他(她)偏瘦的概率是多少?
有没有顿时觉得豁然开朗?原来所谓先验概率无非就是正着问,顺着我们逻辑的方式去提问;而后验概率则是逆着我们的逻辑的去问!
2.贝叶斯公式
好的,了解了先验概率与后验概率之后,我们也要尝试去解决这两个问题。
首先对于先验概率问题,我们很容易计算:

而对于后验概率,则稍微复杂一点:

看到后验概率这一部分,这一部分的推演,差不多就是贝叶斯公式的雏形了。我们来看看真正的贝叶斯公式:

如何理解?
我们把P(A)当做随便找一个人,这个人是开荤者的概率,在刚刚那一题中,我们只考虑了有偏瘦与偏胖的人群,然而现实中,可能还有特别瘦的,也有特别胖的,也会有不胖不瘦的,远不止偏瘦和偏胖两种情况。这就让P(A)的求解更加复杂。我们上下乘U,则分母(开荤的总人数)就是一个求和:在不同体质的人数乘该体质下开荤的比重,再将其求和,加起来,得到一个总数。而分子,就是一个条件概率的变形,学过概率论的应该都能变形出来,乘上U代表的数学意义为,某体质且开荤的人数。
3、最大后验概率
我们期望将概率结果最大时所对应的值的类别作为输出结果,此时它的概率我们会称之为最大后验概率。
光看定义,我们有“亿”点点难懂。不要急,我们结合例子来看
案例:伍老师所在的学校里偏高和偏矮的人所占比例为3:7,其中有偏矮的人中有60%嫌自己矮,所以穿增高鞋。已知,伍老师不穿增高鞋,且你不知道伍老师的其他信息,那么提问:伍老师更可能偏高还是更可能偏矮?
我相信,看懂了小编上一篇文章的同学们,肯定能飞快的解出此题答案,当然了,这个题目也算是一个小小的课堂作业,同学们可以来检查一下自己是不是理解了后验概率。下面是小编的解题过程:

由这道题目,我们可以看出,伍老师偏高的概率更大,而在实际中,人们更愿意去相信概率高的事件,我们更愿意去相信伍老师偏高,尽管在不穿增高鞋的情况下,偏高的概率仅仅比偏矮的概率高一点点。此时不穿增高鞋,伍老师偏高的概率,我们称之为最大后验概率。而它对应的属性,即偏高,是更能使我们信服的属性,即输出结果(y*)。
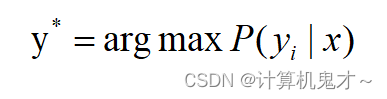
如上图的公式,有人不理解argmax是什么意思,小编这里解释一下,x=argmaxf(x)代表着先去求一个最大的f(x),将它对应的x作为输出结果求出。
4、最大似然估计法
这一部分学过概率论的同学会比较轻松,没有学过概率论的同学可以听我慢慢讲解。
最大似然估计方法(也称为最大概似估计或极大似然估计),是求估计参数的方法之一。
用人话说那就是,极大似然估计就是给定模型,然后收集样本,估求该模型的参数。
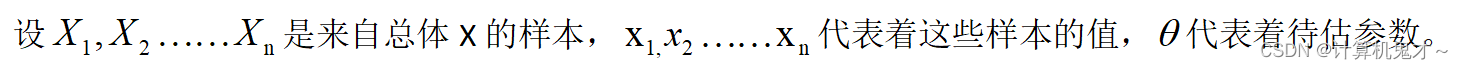
用例子来表示就是,假如我们想要求出伍老师所在学校的人偏高的比例θ,则X代表着全校师生,X1,X2……Xn代表着张三,李四……王二麻子(有点不像学生的名字,将就着看吧),x1,x2……xn代表着偏矮,偏高……偏矮。(注意大小写X,x)
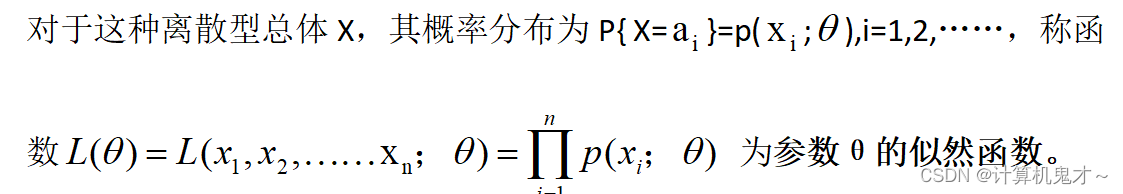
什么意思?估计很多同学都有点一头雾水的感觉。就是用通过x1,x2……xn算出来的θ,再求一遍Xi=xi发生的概率,让样本中的每个点用θ求出的概率,最终让这些概率相乘,乘出的有关θ的表达式即为参数θ的似然函数。
我们当然期望这个似然函数越大越好,于是乎,我们需要求出似然函数处于最大值时,参数θ的大小。即:
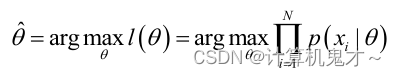
为了求出它的最大值,我们想到,可以利用好求导的方法:

举个小小的栗子,抛硬币大家都玩过吧?如果我抛了五次,三次朝下,两次朝上,请用极大似然估计硬币朝上的概率θ。
很多人的第一印象就是0.5,正面与反面各占一半不是天经地义嘛?拜托,别太死心眼了,我们这是在做题!
也就是说,利用这几个样本与极大似然估计法估计参数θ最合理的解是0.4!

想要了解机器学习与贝叶斯公式有何关联,关注我,下一篇文章更精彩!