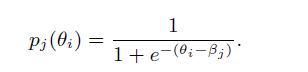1、IRT模型概述　　

　　IRT（item response theory 项目反映理论）模型。IRT模型用来描述被试者能力和项目特性之间的关系。在现实生活中，由于被试者的能力不能通过可观测的数据进行描述，所以IRT模型用一个潜变量 θθ 来表示，并考虑与项目相关的一组参数来分析正确回答测试项目的概率。目前常见的IRT模型有2-PL模型和3-PL模型。其具体表达式如下：

　　2-PL模型的表达式如下：

　　　　pi,j(θi)=11+exp[−Daj(θi−bj)]pi,j(θi)=11+exp[−Daj(θi−bj)]

　　其种 θiθi 是被试者能力的参数，ajaj  和 bjbj 分别代表的是题目的区分度参数和难度参数，D是为1.7的常数。

　　3-PL模型是在模型中引入了预测参数 cjcj ，该参数的含义是描述被试者在没有任何先验知识的情况下，回答正确某项目的概率。常见的例子有学生在做选择题时，即使对该问题没有任何相关知识的获取，也有一定的概率答对该题目。

　　3-PL模型的表达式如下：

　　　　pi,j(θi)=cj+1−cj1+exp[−Daj(θi−bj)]pi,j(θi)=cj+1−cj1+exp[−Daj(θi−bj)]

　　cjcj 表示的是预测参数，其余的参数含义和2-PL模型中的一致。

　　IRT模型满足三条基本假设：

　　1）潜在单调性，IRT模型是连续严格单调的函数。

　　2）条件独立性，IRT模型认为给定 θiθi，对于第 ii 个被试者，Yi,jYi,j 是独立的；而对于不同的被试者，其各自的答案 YiYi 也是相互独立的。

　　3）单维性假设，IRT模型认为某个测试的所有项目都是测量同一个潜在特质。

　　IRT模型的曲线又称为项目相应曲线或者项目特征曲线（ICC），曲线图如下：

　　　　

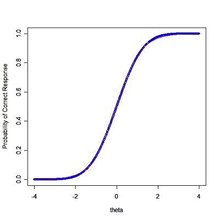
　　区分度参数 aa 的值是ICC曲线拐点处的斜率，即斜率的最大值。项目难度参数 bb 一般表示在ICC曲线最陡的那一点所对应的 θθ 的值。改变 bb 的值不会改线曲线的形状，只会导致曲线左右移动。预测参数 cc 代表了ICC曲线的下限，如上图 cc 的值为0.

　　在这里为了方便讨论，我们用2-PL模型来作为示例。而实际情况中为了简化模型，也可以将预测参数设置为一个常数，例如对于主观题设置为0，对于选择题设置为0.25.

 2、EM算法求解IRT模型

　　EM算法的具体讲解见这一篇。EM算法是一种迭代算法，用于含有隐变量的概率模型的极大似然估计，或者说是极大后验概率估计。EM算法分为 E步和 M步

　　E步：计算联合分布的条件概率期望。

　　M步：极大化对数似然函数的条件期望求解参数。

　　首先来分析我们的观测数据和隐变量。

　　观测数据：我们把被试者 ii 对项目 jj 的作答反映记为 yi,jyi,j ，又记向量 yi=(yi1,yi2,.....,yim)yi=(yi1,yi2,.....,yim) ，称为观测数据，其中 i=1,2,...,N,j=1,2,...,mi=1,2,...,N,j=1,2,...,m。对于两级计分模型（在这里我们只考虑两级计分模型，即模型输出的结果只有二分类），yijyij 的取值有0 和 1，分别表示被试者答错和答对题目。除了两级计分模型，还会有多级计分模型（即输出的结果为多分类）。

　　隐变量（缺失数据）：我们把每个被试者的潜在的不可观测的能力值称为缺失数据，记为 θ=(θ1,θ2,......,θN)θ=(θ1,θ2,......,θN) ，其中 θiθi 是被试者 ii 的潜在能力值。

　　完全数据：完全数据对每一个被试者来说就是观察数据加缺失数据，记作 [(y1,θ1),(y2,θ2),...,(yN,θN)][(y1,θ1),(y2,θ2),...,(yN,θN)] 。

　　将EM算法应用到IRT模型中来，则E步和M步可以描述为：

　　E步：即在给定缺失数据的分布，观察数据和参数初值时，求完全数据的对数似然函数的条件期望。

　　M步：即使用E步计算出的完全数据充分统计量的条件期望值，极大化完全数据的对数似然函数的条件期望求解参数的值。

　　不断的循环迭代E步和M步，直到参数估计收敛。

　　在IRT模型当中，我们通常认为能力参数 θθ 是连续随机变量，故可以取任意值。在EM算法估计参数的过程中，我们是能力参数 θθ 为离散分布。能力值只能取 q1,q2,......,qKq1,q2,......,qK, K个值中的一个，且 P(θ=qk)=πkP(θ=qk)=πk 。

　　 在给定了反应矩阵 YY 的情况下，假设项目参数 Δ=[δ1,......,δJ]Δ=[δ1,......,δJ] ，能力分布参数 π=(Π1,......,ΠK)π=(Π1,......,ΠK) 。则E步中计算的条件期望推到如下：

　　　　

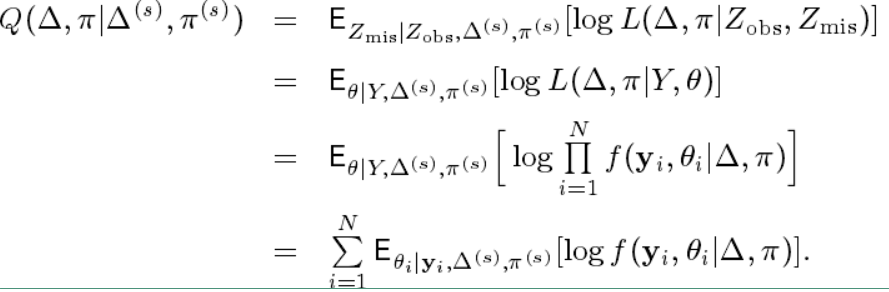
　　对上面的公式做一些转换表示为：

　　　　

　　其中 ϕ(Δ)ϕ(Δ) 和 ψ(π)ψ(π) 的表达式如下：

　　　　

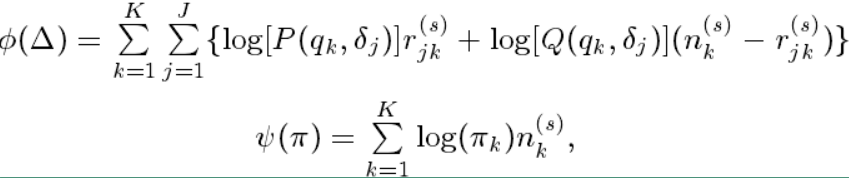
　　其中：

　　　　

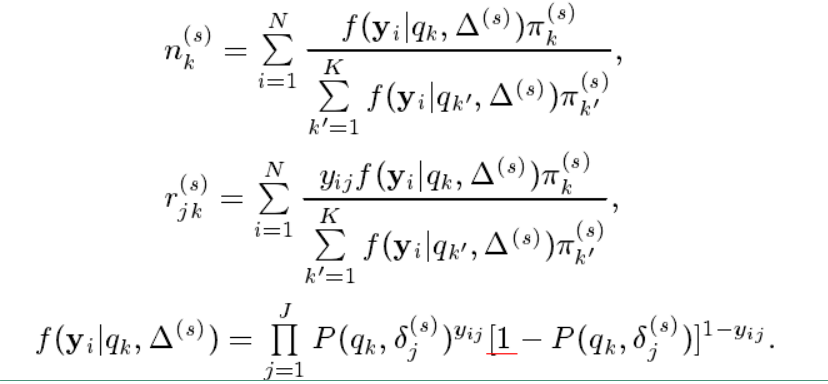
　　在上面式子中的 n(s)knk(s) 可以理解为在 NN 个被试者中能力水平为 qkqk 的被试数目的期望（即能力为 qkqk 的被试者的个数），r(s)jkrjk(s) 可以理解为在 NN 个被试者中具有能力水平 qkqk 的被试者答对第 jj 个项目的个数。 n(s)knk(s) 和 r(s)jkrjk(s) 都是人工数据。

　　应用EM算法的第 ss 步迭代中

　　E步：利用第 s−1s−1 步得到的参数估计值 Δ(s)Δ(s) 和 π(s)kπk(s) 计算 n(s)knk(s) 和 r(s)jkrjk(s) （首次迭代时初始化 Δ(0)Δ(0) 和 π(0)kπk(0) 的值）。

　　M步：将E步计算出的 n(s)knk(s) 和 r(s)jkrjk(s) 代入到 ϕ(Δ)ϕ(Δ) 和 ψ(π)ψ(π) 中，对两项分别极大化可得参数 ΔΔ 和 ππ 的估计值 Δ(s+1)Δ(s+1) 和 π(s+1)kπk(s+1) .具体的求解如下：

　　　　

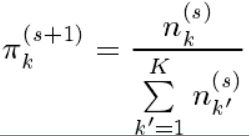
　　π(s+1)kπk(s+1) 的值可以直接用上述表达式求出

　　而对于 Δ(s+1)Δ(s+1) 在这里要用牛顿-拉弗逊方法求解。

　　EM算法估计IRT模型的步骤如下：

　　1）E步：

　　　　首先确定 qkqk 和 πkπk ；用前一次迭代参数 Δ(s)Δ(s) 和 π(s)kπk(s) 求出 n(s)knk(s) 和 r(s)jkrjk(s) 。

　　2）M步：

　　　　计算 δ(s+1)jδj(s+1) 和 π(s+1)π(s+1) .

　　3) 重复E步和M步直到项目参数收敛为止。

 3、MCMC算法求解IRT模型

　　MCMC算法的具体详解见这一篇，MCMC算法全称是马尔科夫-蒙特卡洛算法。MCMC的基础理论为马尔可夫过程，在MCMC算法中，为了在一个指定的分布上采样，根据马尔可夫过程，首先从任一状态出发，模拟马尔可夫过程，不断进行状态转移，最终收敛到平稳分布。用MCMC算法在这里估计参数，事实上就是建立一条参数的马尔科夫链，根据参数的状态转移矩阵来输出马尔科夫链上的样本，当马尔科夫链到一定长度时就会开始收敛于某一值。

　　首先来看看MCMC算法在2-PL模型上的参数估计步骤：

　　1）取模型参数的先验分布：θ N(0,1)，log(a) N(0,1)，b N(0,1)θ N(0,1)，log⁡(a) N(0,1)，b N(0,1) ，则初始化被试能力参数，项目参数的初始值 θ0=0，a0=1，b0=0θ0=0，a0=1，b0=0 。

　　2）根据项目参数初值 a0，b0a0，b0 ，估计被试者的能力参数 θ1θ1 。

　　　  各被试的能力参数 θ∗θ∗ 独立地从建议性分布 qθqθ 中选取，我们去被试能力参数的建议分布为 θ∗ N(θ0,c2θ)θ∗ N(θ0,cθ2) 。其中 一般cθ=1.1cθ=1.1。

　　　  计算从状态 θ0θ0 转移到状态 θ1θ1 的接受概率 a(θ0,θ∗)=min(1,R0θ)a(θ0,θ∗)=min(1,Rθ0)，由它来决定是否发生状态的转移。

　　　　

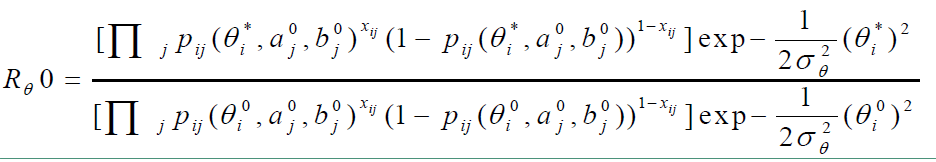
　　　  其中

　　　　

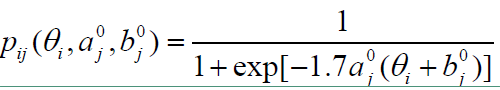
　　　  生成随机数 r1 U(0,1)r1 U(0,1) ，比较 r1r1 与接受概率 a(θ0,θ∗)a(θ0,θ∗) 的大小，进行状态转移判断：

　　　　若 a(θ0,θ∗)≥r1a(θ0,θ∗)≥r1 ，则有 θ1=θ∗θ1=θ∗ ；否则 θ1=θ∗θ1=θ∗ 。

　　3）根据步骤（2）计算出来的被试能力参数 θ1θ1 ，估计项目参数 a1,b1a1,b1 。

　　      各项目的区分度参数和难度参数 a∗,b∗a∗,b∗ 分别独立地从建议分布 qa,qbqa,qb 中选取，我们取区分度参数和难度参数的建议分布为 log(a∗) N(a0,c2a),b∗ N(b0,c2b)log⁡(a∗) N(a0,ca2),b∗ N(b0,cb2) ，其中 ca=0.3,cb=0.3ca=0.3,cb=0.3 。

　　　  计算从状态 (a0,b0)(a0,b0) 转移至状态 (a∗,b∗)(a∗,b∗) 的接收概率 α(a0,b0,a∗,b∗)=min(1,R0a,b)α(a0,b0,a∗,b∗)=min(1,Ra,b0) ，由它来决定是否发生状态的转移。

　　　　

　　　  其中

　　　　

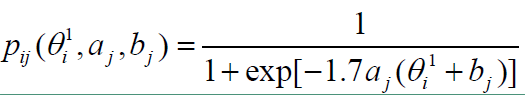
　　　  生成随机数 r2 U(0,1)r2 U(0,1) ，比较 r2r2 与 α(a0,b0,a∗,b∗)α(a0,b0,a∗,b∗) 的大小，进行状态转移判断：

　　　  若 α(a0,b0,a∗,b∗)≥r2α(a0,b0,a∗,b∗)≥r2 ，则 a1=a∗,b1=b∗a1=a∗,b1=b∗ ；否则 a1=a0,b1=b0a1=a0,b1=b0 。

　　4）重复步骤（2）和（3）nn 次，删除为首的 ww 次，取剩余的 m=n−wm=n−w 次迭代所得结果的均值即为参数的估计值。

　　5）步骤（4）会生成一条长度为 nn 的 MarkovMarkov 链，重复步骤（4）ii 次（ ii 次一般小于5），即可以得到 ii 条 MarkovMarkov 链，将这 ii 条链得到的参数估计值的均值为最终的参数估计值。

　　MCMC 算法在求解3-PL模型的参数时和求2-PL模型的参数的方法一致。但是在同等的数据量下，3-PL模型的参数估计精度要低于2-PL模型的参数估计的精度（参数越多，模型越复杂，在同等量的参数下就更容易过拟合）。因此一般我们会将预测参数 cjcj 标为常数值。

4、4-PL模型

　　在3-PL模型中引入预测参数 cjcj 是为了描述被试者在没有任何相关项目能力地情况下，答对项目的概率。然而现实中还会存在一种情况就是被试者在充分掌握了项目知识的情况下，可以认为理论上被试者关于此项目的能力是完全可以答对该项目的，但实际中却答错了该问题。为了解决这一问题，引入了参数 γjγj ，此时模型可以表示为：

　　pi,j(θi)=cj+γj−cj1+exp[−Daj(θi−bj)]pi,j(θi)=cj+γj−cj1+exp[−Daj(θi−bj)]

　　对于4-PL模型的参数估计依然可以用估计2-PL参数的方法，此时项目参数不再只是 (aj,bj)(aj,bj) ，而是 (aj,bj,cj,γj)(aj,bj,cj,γj) 。